केन्द्रवर्ती मानों से आप क्या समझते हैं ? मध्यमान एवं मध्यांक ज्ञात करने की विभिन्न विधियों को उदाहरण सहित समझाइये ।

उत्तर–केन्द्रवर्ती मान (Central Tendency) — विस्तृत आँकड़ों को सार्थक तथा विश्लेषण योग्य बनाने के लिए केवल व्यवस्थापन तथा आलेखी निरूपण ही पर्याप्त नहीं होता है अपितु उनके केन्द्रीय प्रवृत्ति का पता लगाना भी आवश्यक होता है। केन्द्रीय प्रवृत्ति का अभिप्राय उस संख्यात्मक माप से है जो कि प्राप्त आँकड़ों का सबसे अधिक प्रतिनिधित्व करता है अर्थात् वह मान जो प्राप्त आँकड़ों के पदों में बार-बार आता है। साधारण भाषा में केन्द्रीय प्रवृत्ति से आशय औसत से लगाया जाता है।

केन्द्रीय प्रवृत्ति को स्पष्ट रूप से समझने के लिए हमें इसकी कुछ परिभाषाओं का अध्ययन करना होगा—

डॉ. रामपालसिंह वर्मा व रामवालभ उपाध्याय के अनुसार, “केन्द्रीय प्रवृत्ति से तात्पर्य उस संख्या से है जिसके चारों ओर समूह के सभी अंक छाये रहते हैं। साधारण भाषा में केन्द्रीय प्रवृत्तियों को हम माध्य (Average) की संज्ञा दे सकते हैं।”

के. एल. राय एवं श्रीमती शर्मा ने केन्द्रीय प्रवृत्ति को परिभाषित करते हुए लिखा है— “किसी समूह के ज्ञान के लिए हम एक प्रतिनिधि का चयन करते हैं जो उस समूह के अधिकतर लोगों के विषय में ज्ञान प्रदान करता है। इसी प्रकार सांख्यिकी में भी उस प्राप्तांक का पता लगाया जाता है जो कि सम्पूर्ण प्राप्तांकों के विषय में ज्ञान प्रदान करता है। सांख्यिकी में इस प्रकार का वर्णन करने हेतु केन्द्रीय मान ज्ञात किया जाता है। इस केन्द्रीय मान को साधारण भाषा में औसत (Average) शब्द के द्वारा प्रकट किया जाता है।”

उपर्युक्त परिभाषाओं से स्पष्ट होता है कि केन्द्रीय प्रवृत्ति के मान से आशय ऐसे मानों से है जो सम्पूर्ण प्राप्तांकों का प्रतिनिधित्व करते हैं, दूसरे शब्दों में प्राप्तांकों के औसत को केन्द्रीय प्रवृत्ति के माप के रूप में स्पष्ट किया जाता है।

केन्द्रीय प्रवृतित के माप (Measures of Central Tendency)– केन्द्रीय प्रवृत्ति के मानों का हम निम्नलिखित रूप में अध्ययन कर सकते हैं—

(1) मध्यमान (Mean), (2) मध्यांक (Mediam), (3) बहुलांक (Mode), (4) गुणोत्तर मध्यमान (Geometric Mean), (5) हरात्मक मध्यमान (Harmonic Mean)।

मध्यमान की गणना (Computation of Mean)– मध्यमान की गणना अव्यवस्थित एवं व्यवस्थित दोनों प्रकार के समंकों में की जा सकती है। इस अव्यवस्थित एवं व्यवस्थित दोनों प्रकार के समंकों के मध्यमान की गणना का अध्ययन अलग-अलग करेंगे।

(i) अव्यवस्थित समंकों से मध्यमान की गणना (Form Unground Data) – जब प्रतिदर्श छोटा हो तो अव्यवस्थित समंकों से मध्यमान की गणना की जाती है। इस प्रकार के समंकों की गणना के लिए सर्वप्रथम दिये गये मूल्यों या अंकों का योग कर लिया जाता है तथा इसके बाद योग में मदों की संख्या का भाग दे दिया जाता है। इस गणना के लिये निम्नलिखित सूत्र का प्रयोग किया जाता है

उदाहरणार्थ– एक कक्षा के 10 विद्यार्थियों को गणित विषय में 10 में से क्रमशः 8, 5, 7, 5, 4, 6, 5, 6, 6 तथा 8 अंक प्राप्त हुए हैं छात्रों के द्वारा प्राप्त अंकों का मध्यमान ज्ञात कीजिए।

मध्यमान (Mean)—

(ii) व्यवस्थित समंकों से मध्यमान की गणना (From Grouped Data)–समंकों को व्यवस्थित दो प्रकार से किया जा सकता है—

(अ) खण्डित श्रेणी में मध्यमान की गणना (Mean in Discrete Series )—अव्यवस्थित समंकों में कुछ अथवा सभी मदों के मूल्य अधिक बार दिये होने पर उन्हें खण्डित श्रेणी में रूप में व्यवस्थित कर सकते हैं। इस श्रेणी में मध्यमान की गणना के लिए दो विधियाँ हैं–

( 1 ) प्रत्यक्ष विधि (Direct Method) — इस विधि से मध्यमान को गणना करने के लिए सर्वप्रथम प्रत्येक मद के मूल्य को उसकी आवृत्ति से गुणा करते हैं, इसके पश्चात् सभी गुणनफलों का योग कर, योग में आवृत्तियों के योग का भाग दे दिया जाता है। इस विधि से मध्यमान ज्ञात करने का निम्नलिखित सूत्र हैं—

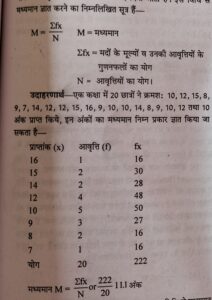
(2) लघु लिपि (Short cut Method)—इस विधि से मध्यमान की गणना करने के लिए मदों के मूल्यों (X) में से किसी को कल्पित मध्यमान मानकर विचलन ज्ञात किये जाते हैं, इनके लिए X के प्रत्येक मूल्य में से कल्पित माध्य को घटाया जाता है। विचलन निकालने के बाद उन्हें आवृत्तियों से गुणा किया जाता है और फिर निम्नलिखित सूत्र की सहायता से मध्यमान ज्ञात कर लिया है—

(आ) अखण्डित अथवा सतत् श्रेणी में मध्यमान की गणना (Mean in Continuous series)—अखण्डित श्रेणी में मध्यमान की गणना की दो विधियाँ हैं—

( 1 ) प्रत्यक्ष विधि (Direct Method)—सतत् श्रेणी में मध्यमान ज्ञात करने के लिए वर्गान्तरों के मध्य बिन्दु निकाले जाते हैं, यह निकालने के लिए वर्गान्तर की निम्न एवं उच्च सीमा को जोड़कर 2 का भाग देते दे देते हैं। इस मध्य बिन्दु को ‘x’ का मूल्य मानते हैं। इसके पश्चात् मध्यमान की गणना के लिए सम्पूर्ण प्रक्रिया वही अपनाते हैं, जो खण्डित श्रेणी में प्रत्यक्ष विधि से निकालने के लिए अपनाई जाती है। मध्यमान की गणना का इस श्रेणी में भी वही सूत्र है, जो खण्डित श्रेणी में प्रत्यक्ष विधि के अनुसार था —

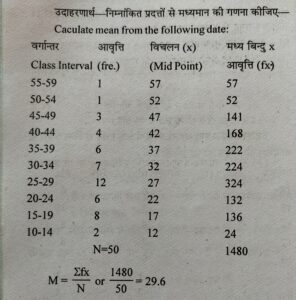
( 2 ) लघु विधि (Short cut Method) — सतत् श्रेणी में लघु विधि से मध्यमान निकालने के लिए निम्न प्रक्रिया अपनानी होती है(i) सर्वप्रथम वर्गान्तरों के मध्य बिन्दु ज्ञात कर लिये जाते हैं। मध्य बिन्दु ज्ञात करने की वही विधि है जो प्रत्यक्ष विधि में है। ये मध्य बिन्दु ही मद (x) के मूल्य होते हैं ।

(ii) मध्य बिन्दुओं में किसी भी मूल्य को कल्पित मध्यमान मानकर उसकी सहायता से ‘x’ के सभी मूल्यों के विचलन (dx) ज्ञात किये जाते हैं। विचलन ज्ञात करने के लिए x के मूल्यों में से कल्पित मध्यमान को घटाकर, उसमें वर्ग अन्तराल का भाग देते हैं।

(iii) प्राप्त विचलनों (dx) को सम्बन्धित आवृत्तियों (f) से गुणा करते हैं और प्राप्त गुणनफलों का योग (Lfdx) कर लिया जाता है।

इसके पश्चात् निम्न सूत्र की सहायता से मध्यमान की गणना कर ली जाती है—

मध्यांक की गणना (Computation of Median)—मध्यमान की भांति मध्यांक की गणना भी अव्यस्थित एवं व्यवस्थित दोनों प्रकार के प्रदत्तों से की जा सकती है। मध्यांक की गणना दोनों ही प्रकार के समंकों से निम्न प्रकार की जा सकती है—

(i) अव्यवस्थित समंकों से मध्यांक की गणना (From Ungrouped Data)—मदों की संख्या कम होने पर मध्यमान की भाँति ही मध्यांक की गणना भी अव्यवस्थित समंकों को बिना व्यवस्थित किये ही कर ली जाती है। मध्यांक की गणना करने के लिए सर्वप्रथम मदों को निश्चित क्रम (आरोही अथवा अवरोही) में रख दिया जाता है इसके पश्चात् मदों की संख्या (N) में 1 जोड़कर उसमें दो का भाग दे दिया जाता है और प्राप्त पद पर x का जो मूल्य दिया हुआ होता है वही मूल्य मध्यांक होता है। इसका सूत्र निम्नलिखित हैं—

(ii) व्यवस्थित समंकों से मध्यांक की गणना (From Gropued Data)—समंकों को व्यवस्थित करने की दृष्टि से दो प्रकार की श्रेणियाँ खण्डित अथवा सतत् श्रेणी बनाई जा सकती है। दोनों प्रकार के श्रेणियों से. मध्यांक की गणना निम्न प्रकार से की जा सकती है—

(अ) खण्डित श्रेणी में मध्यांक की गणना (In Discrete Series ) — खण्डित श्रेणी में मध्यांक ज्ञात करने के लिए निम्नलिखित प्रक्रिया अपनाई जाती है—

(1) श्रेणी को आरोही अथवा अवरोही क्रम में व्यवस्थित करते हैं।

(2) श्रेणी की आवृत्तियों से संचयी आवृत्तियाँ ज्ञात करते हैं ।

(3) संचयी आवृत्तियाँ ज्ञात करने के पश्चात् निम्नलिखित सूत्र का प्रयोग करते हैं—

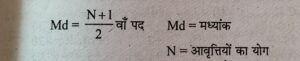
(4) उपरोक्त सूत्र की सहायता से ज्ञात … वाँ पद को संचयी आवृत्ति में देखते हैं, वाँ पद संचयी आवृति के जिन समूह में आता है उसके सामने वाले X मूल्य को देखते है, यहाँ X का मूल्य मध्यांक का मल्य होगा।

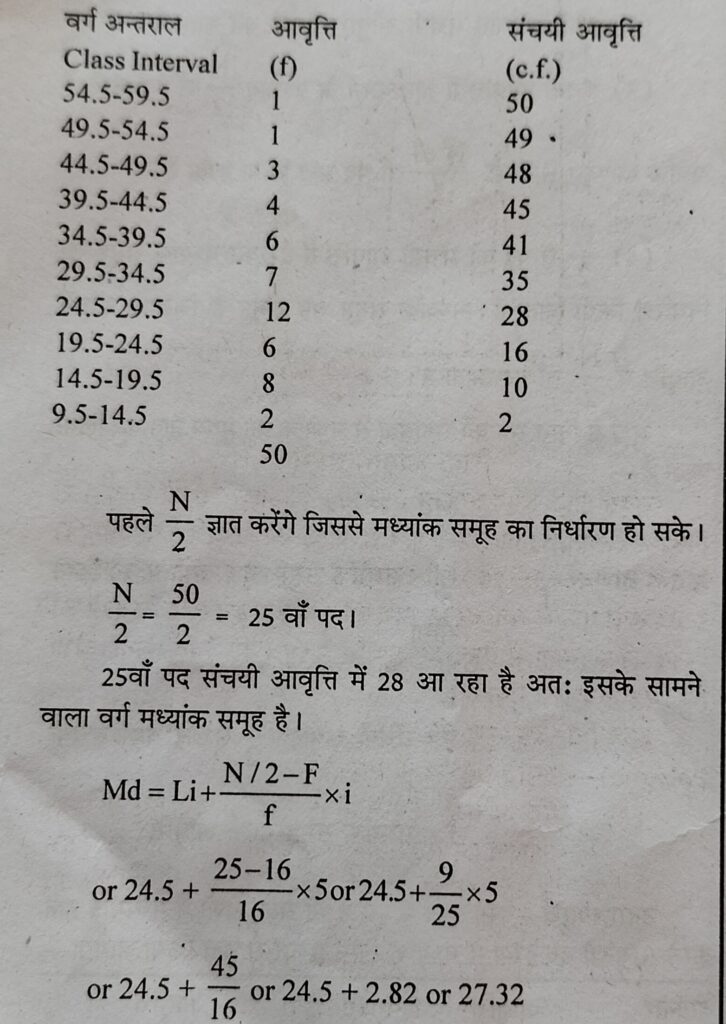
उपर्युक्त श्रेणी समावेशी है अतः पहले उसे अपवर्जी श्रेणी में परिवर्तित करना होगा। चूँकि यह श्रेणी अवरोही क्रम में है। अतः समावेशी श्रेणी से अपवर्जी श्रेणी में बदलने के लिए प्रस्तुत श्रेणी के प्रथम वर्ग को निम्न सीमा तथा दूसरे वर्ग की उच्च सीमा में अन्तर देखा जायेगा, यह अन्तर 1 है इसमें 2 का भाग देने पर 5 आयेगा । इस 5 को श्रेणी के सभी वर्गों की निम्न सीमाओं में से घटाने तथा उच्च सीमाओं में जोड़ने पर प्राप्त श्रेणी अपवर्जी श्रेणी में बदलने के बाद मध्यांक निम्न प्रकार ज्ञात किया जायेगा—