अवतल दर्पण में सिद्ध करें कि f=R/2 जहाँ f और R के विशिष्ट मान है।

अवतल दर्पण में सिद्ध करें कि f=R/2 जहाँ f और R के विशिष्ट मान है।

उत्तर⇒ 

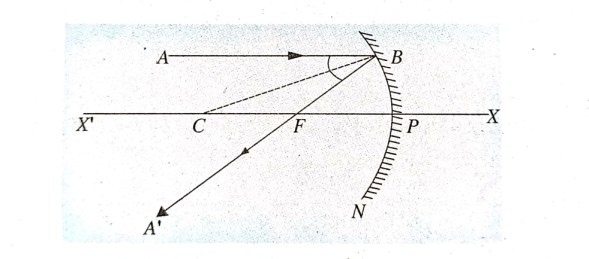
AB प्रकाश किरण मुख्य अक्ष के समांतर है। AB किरण दर्पण से परावर्तन के बाद F (फोकस) से होकर गुजरता है। CB को मिलाया गया है।

∠ABC = ∠CBF = ∠i = ∠r 

इसलिए  AB \\XX ‘ 

∠CBF = ∠ABC = ∠BCF 

इसलिए ∠i = ∠r 

इसलिए  अत: CF = BF 

अगर B बिन्दु P के काफी समीप है तो BF = PF

इसलिए CP = PF = f (फोकसान्तर)  CP = R अवतल दर्पण की वक्रता त्रिज्या है।

इसलिए CP = CF + PF

R= f +f = 2f

इसलिए  R = 2f

अतः वक्रता त्रिज्या = 2 x फोकसान्तर