Bihar Board Class 9Th Mathematics chapter 1 संख्या पद्धति (Number System) Solutions | Bseb class 9Th Chapter 1 संख्या पद्धति (Number System) Notes
Bihar Board Class 9Th Mathematics chapter 1 संख्या पद्धति (Number System) Solutions | Bseb class 9Th Chapter 1 संख्या पद्धति (Number System) Notes
प्रश्न- परिमेय संख्या (Rational Number) किसे कहते हैं ?
उत्तर— वह संख्या जिसे P/Q के रूप में लिखा जा सके जहाँ P और Q एक पूर्णांक (Integer) हो तथा Q शून्य के बराबर न हो (Q ≠ 0) परिमेय संख्या कहलाती है।
प्रश्न- क्या शून्य एक परिमेय संख्या है ?
उत्तर— हाँ क्योंकि शून्य को हम P/Q = 0/1, 0/2 आदि के रूप में लिख सकते हैं अतः यह परिमेय है।
प्रश्न- 2 और 3 के बीच तीन परिमेय संख्या ज्ञात करें।
उत्तर— माना कि, a = 2 और b = 3
कुल परिमेय संख्या जो ज्ञात करनी है, n = 3
अत:, d = b – a / n + 1= 3 – 2 / 3 + 1= 1/4
अतः 2 और 3 के बीच की परिमेय संख्या होगी—
2 + 1/4, 2 + 2/4, 2 + 3/4 ⇒ 9/4, 10/4, 11/4
प्रश्न- 3 और 4 के बीच छः परिमेय संख्या ज्ञात करें ।
उत्तर— माना कि, a = 3 और b =4
कुल परिमेय संख्या, n = 6
अतः d = b – a / n + 1 = 4 – 3 / 6 + 1 = 1/7
अतः 3 और 4 के बीच की परिमेय संख्या होगी
3 + 1/7, 3 + 2/7, 3 + 3/7, 3 + 4/7, 3 + 5/7, 3 + 6/7
= 22/7, 23/7, 24/7, 25/7, 26/7, 27/7
प्रश्न- 3/5 और 4/5 के बीच पाँच परिमेय संख्या ज्ञात करें :
उत्तर— माना कि, बड़ी संख्या b = 4/5 छोटी संख्या a = 3/5
कुल परिमेय संख्या n = 5
अतः d = b – a / n + 1 = 4/5 – 3/5 / 5 + 6 = 1/ 5 x 6 = 1/30
अतः अभीष्ट परिमेय संख्या होगी
3/5 + 1/30, 3/5 + 2/30, 3/5 + 3/30, 3/5 + 4/30 , 3/5 + 5/30
⇒ 19/30, 20/30, 21/30, 22/30, 23/30
प्रश्न- √5 को संख्या रेखा पर निरूपित करें :
(i) एक सीधी रेखा ‘ I ‘ लें ।
(ii) रेखा I पर AB = 2 ईकाई ले ।
(iii) बिंदु B से रेखा I पर लम्ब ‘m’ डालें ।
(iv) BC = 1 इकाई काटे ।
(v) A को C से मिला दे ।
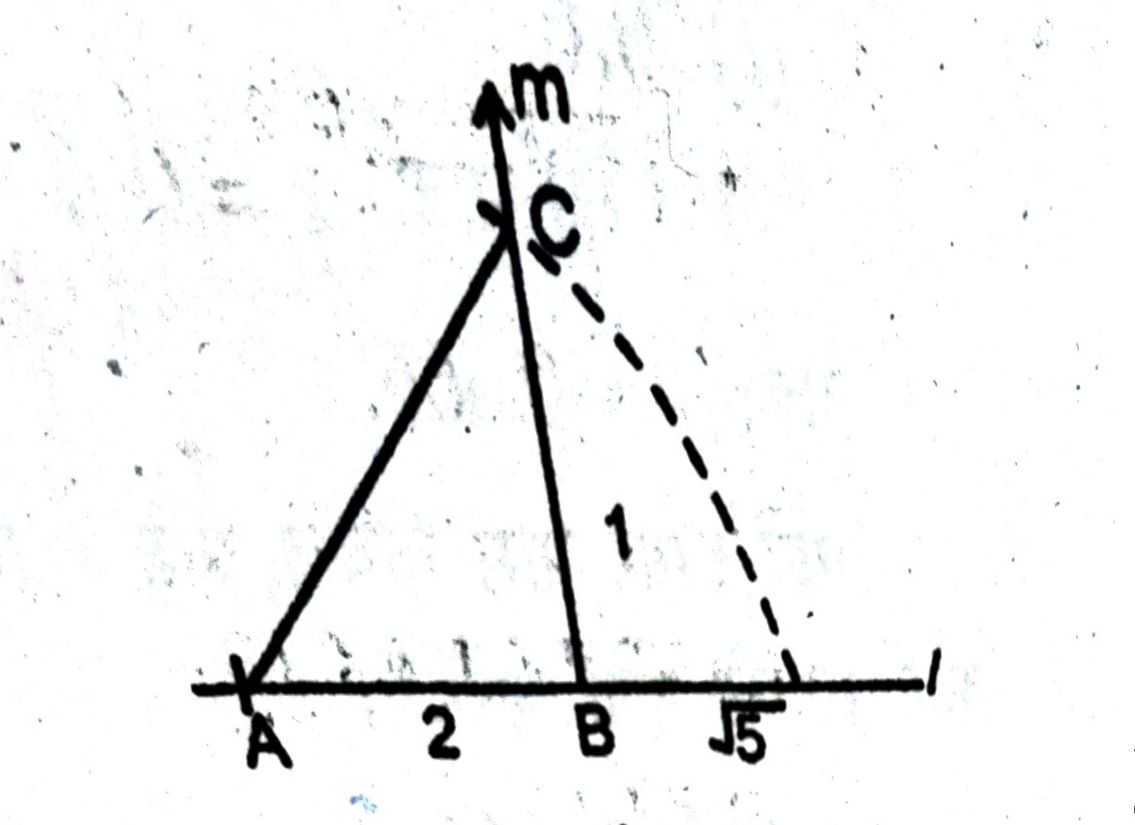
अतः समकोण त्रिभुज ΔABC में
AC = √AB² + BC² (पाइथागोरस प्रमेय से)
= √(2)² + (1)² = √5
अब A को केन्द्र मानकर AC त्रिज्या (Radius) का एक वृत चाप खिचें। और रेखा I को काटे । यह बिंदु √5 होगी ।
प्रश्न- निम्न को दशमलव रूप में लिखें और बताये की वो सांत है या असतं ।
(i) 36/100 (ii) 1/11 (iii) 4 – 1/8 (iv) 3/13
(v) 2/11 (vi) 329/400 (vii) 16/28
(viii) 1/125
उत्तर— (i) 36/100 ⇒ 100) 360 ( 0.36
300
———
x 600 ⇒ सांत, दशमलव
600
———
xxx
(ii) 1/11⇒ 11) 100 ( 0.09090….
99
——
x 100 = 0.0909… ⇒ असांत दशमलव
99
——
x 10
(iii) 4.125 सांत
(iv) 3/13 = 13) 30 ( .230769
26
——
x 40
39
——
x 100 = 0.230768 ⇒ असांत दशमलव
91
——
x 90
78
——
120
117
——
x 3
(v) 0.18 असांत (vi) 0.8225, सांत
(vii) 0.571428….. (viii) 0.008 स्वयं से भाग बनायें l
प्रश्न- निम्नलिखित को p/q के रूप में व्यक्त कीजिए, जहाँ p और q एक पूर्णांक हैं तथा q ≠ 0 है
(i) 0.6 (ii) 0.47 (iii) 0.001
उत्तर— हल : (i) माना x = 0.6
तब, x = 0.666… …(1)
यहाँ हमारे पास केवल एक आवृत्ति अंक है अतः हम समी० (1) को दोनों ओर 10 से गुणा करेंगे ।
10x = 6.66….
(2) में से (1) घटाने पर
10x – x = (6.66…) – (0.66…)
⇒ 9 x = 6 = x = 2/3
अतः 0.6 = 2/3
(ii) माना x = 0.47
हम दोनों ओर 10 से गुणा करेंगे ताकि दशमलव के बाद केवल आवृति (Repeated) अंक बचें।
∴ 10x=4.7=4.777…. …(i)
पुन: x को 100 से गुणा करने पर
10 x = 47.777…. …(ii)
समी० (ii) में से (i) घटाने पर
100 x – 10 x = (47.777…..) – (4.777 ….)
Or, 90 x = 43
अतः x = 43/90
(iii) माना x = 0.001
x=0.001001001… …(1)
यहाँ दशमलव बिन्दु के बाद तीन आवृत्ति अंक हैं । अतः समी० (1) को 1000 से गुणा करेंगे ।
1000x = 1.001001… …(2)
समी० (2) में से (1) घटाने पर
1000x – x = (1.001001…) – (0.001001…)
= 999x = 1 = x = 1/999
अतः 0.001 = 1/999
प्रश्न- ऐसी तीन संख्याएँ लिखिए जिनके दशमलव प्रसार अनवसानी अनावर्ती हों।
उत्तर— हल : 0.1010010001…, 0.2020020002…., 0.303003…..
प्रश्न- परिमेय संख्याओं 5/7 और 9/11के बीच की तीन अलग – अलग अपरिमेय संख्याएँ ज्ञात कीजिए ।
उत्तर— हल : 5/7 = 0.714285 और :: 9/11 = 0.81
अतः 5/7 और 9/11 के बीच तीन अपरिमेय संख्याएँ हैं—
0.75075007500075000075……..
प्रश्न- बताइए कि निम्नलिखित संख्याओं में कौन-कौन संख्याएँ परिमेय और कौन-कौन संख्याएँ अपरिमेय हैं :
(i) √23 (ii) √225 (iii) 0.3796 (iv) 7.478478… (v)1.101001000100001…
उत्तर— हल :
(i) अपरिमेय (ii) परिमेय, क्योंकि √225 = 15
(iii) परिमेय (सांत दशमलव ) (iv) परिमेय (असांत दशमलव) (v) अपरिमेय (अनवसानी अनावर्ती )
प्रश्न- उत्तरोत्तर आवर्धन करके संख्या रेखा पर 3.765 को देखिए ।
उत्तर—

प्रश्न- बताइए नीचे दी गई संख्याओं में कौन-कौन परिमेय हैं और कौन-कौन अपरिमेय हैं :
(i) 2 – √5 (ii) (3 + √23) – √23 (iii) 2√7/ 7√7 (iv) 1/√2 (v) 2π
उत्तर— हल : (i) 2 – √5 एक अपरिमेय संख्या है क्योंकि यह परिमेय और अपरिमेय संख्या का अन्तर है।
(ii) (3+√23) – √23 = 3 + √23 – √23 = 3, जो परिमेय संख्या है।
(iii) 2√7 / 7√7 = 2/7 , जो एक परिमेय संख्या है।
(iv) 1/√2 एक अपरिमेय है क्योंकि परिमेय और अपरिमेय का भागफल है ।
(v) 2π एक अपरिमेय, परिमेय और अपरिमेय संख्या का गुणनफल है ।
प्रश्न- निम्नलिखित व्यंजकों में से प्रत्येक व्यंजक को सरल कीजिए:
(i) (3 + √3) (2 + √2) (ii) (3 + √3) (3 – √3)
(iii) (√5 + √2)² (iv) (√5 – √2) ( √5 + √2)
उत्तर— हल : (i) (3 + √3) (2 + √2) = 3 x 2 + 3 √2 + 2 √3 + √2 x √3
= 6 + 3√2 + 2√3 + √6
(ii) (3 + √3) (3 – √3) = (3)² – (√3)² = 9 – 3 = 6
(iii) (√5 + √2)² = (√5)² + 2√5 √2 + (√2)²
= 5 + 2 √10 + 2 = 7 + 2√10
(vi) (√5 – √2) (√5 + √2) = (√5)² – (√2)² = 5 – 2 = 3
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here