किसी उत्तल दर्पण में सिद्ध करें कि f =R/2 , जहाँ f = फोकसांतर, R = दर्पण की वक्रता त्रिज्या है।
किसी उत्तल दर्पण में सिद्ध करें कि f =R/2 , जहाँ f = फोकसांतर, R = दर्पण की वक्रता त्रिज्या है।
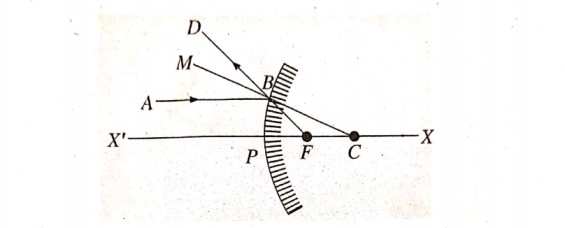
उत्तर⇒ चित्र में एक उत्तल दर्पण को प्रधान अक्ष XX‘ पर रखा गया है। दर्पण का ध्रुव P है। F दर्पण का फोकस और C वक्रता केंद्र है। AB अपवर्तित किरण है। यह दर्पण से परावर्तित होकर BD दिशा में चली जाती है। DB को मिलाने पर यह मुख्य अक्ष के F बिंदु (फोकस) पर मिलाती है। C से B को मिलाया और अपनी दिशा में M तक बढ़ाया गया है।
PF = फोकसांतर =f; PC = वक्रता त्रिज्या = R
अनंत बिंदु से आनेवाली प्रकाश किरण F पर मिलती है
अतः वस्तु का प्रतिबिंब F पर बनता है। यह प्रतिबिंब आभासी है।
∠ABM = i तथा ∠MBD = r
∠i = ∠r परावर्तन के नियम से
∠x = ∠FBC (अंतराभिमुख कोण)
AB || XX’ अतः ∠i = ∠BCF
इसलिए ∠ BCF = ∠FBC
इसलिए BF = FC
अगर B बिंदु P के काफी समीप हैं तो B C = P C
इसलिए BF = PF = FC
PC = PF + FC
R=f +f
इसलिए 2f =R
इसलिए f =R/2
फोकसांतर =1/2 x वक्रता त्रिज्या