Bihar Secondary School Sample Paper Solved | BSEB Class 10th Sample Sets with Answers | Bihar Board class 10th Sample Paper Solved | Bihar Board Class 10th mathematics Sample set – 1
Bihar Secondary School Sample Paper Solved | BSEB Class 10th Sample Sets with Answers | Bihar Board class 10th Sample Paper Solved | Bihar Board Class 10th mathematics Sample set – 1
1. tan (90° – A) = ?
(A) tan A
(B) cot B
(C) sin A
(D) इनमें से कोई नहीं
2. निम्नलिखित में से कौन cosec θ के बराबर है ?
(A) cos θ/ sin θ
(B) 1 / cos θ
(C) 1 / sin θ
(D) sin θ / cos θ
3. निम्न में से कौन किसी घटना की प्रायिकता नहीं हो सकती है ?
(A) 3.5
(B) 0.2
(C) 0.3
(D) 60%
4. यदि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात 64 : 121 है, तो इनके संगत भुजाओं का अनुपात होगा
(A) 8 :11
(B) 8 :12
(C) 12:14
(D) 11 : 8
5. यदि बहुपद p(x) = x2 + 7x + 10 के शून्यक α , β हों तो α · β का मान होगा
(A) –10
(B) 1 / 10
(C) 10
(D) 7 / 10
6. cos π / 3 का मान होगा
(A) 1 / 2
(B) 1 / √3
(C) √3 / 2
(D) √3
7. बहुपद y3 – 2y2 –√3y + 1/2 का घात हैं
(A) 1/2
(B) 2
(C) 3
(D) 3/2
8. किसी वाह्य बिन्दु से एक वृत्त पर कितनी स्पर्श रेखाएँ खींची जा सकती है ?
(A) एक
(B) दो
(C) तीन
(D) इनमें से कोई नहीं
9. निम्नांकित में कौन बहुपद नहीं है ?
(A) √5x2 – 3√2x + 4
(B) x + 1/x
(C) 3x2 – 4x + √5
(D) इनमें से कोई नहीं
10. संचयी बारंबारता वक्र कहलाती है ?
(A) तोरण
(B) आयत चित्र
(C) दण्डालेख
(D) बारंबारता बहुभुज
11. ‘r’ त्रिज्या वाले अर्द्धवृत्त की परिमिति होती है
(A) 2πr
(B) πr
(C) πr + 2r
(D) इनमें से कोई नहीं
12. ΔABC में AB = 6√3 cm; AC = 12cm, BC = 6cm तो ∠B होगा ?
(A) समकोण
(B) अधिक कोण
(C) न्यून कोण
(D) कोई नहीं
13. एक पासे को उछालने पर 3 से बड़ी संख्या आने की प्रायिकता क्या होगी ?
(A) 1/2
(B) 1/6
(C) 3/2
(D) 2/1
14. दो क्रमिक सम संख्याओं का म०स० (HCF) होगा
(A) 1
(B) 2
(C) 3
(D) 5
15. प्रथम 10 सम प्राकृत संख्याओं का माध्य होगा
(A) 110
(B) 11
(C) 10
(D) 100
16. sin 18° / cos 72° का मान होगा
(A) 1/2
(B) 1
(C) √3/2
(D) 0
17. ΔABC में ∠A तथा ∠B पूरक हैं तो cot C का मान होगा
(A) 1√3
(B) 0
(C) 1
(D) √3
18. समीकरण ax2 + bx + c = 0 का विवेचक है
(A) b2 – 2ac
(B) b2 – 3ac
(C) b2 – 4ac
(D) b2 – 5ac
19. दिये गए चित्र में PQ || BC, AP = 2 cm, BP = 6cm, PQ = 3cm हो तो, BC का मान होंगा
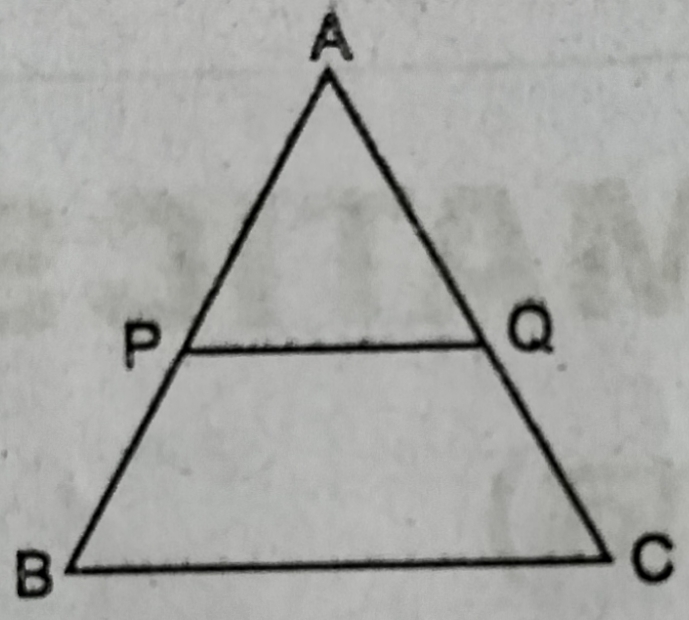
(A) 8cm
(B) 9cm
(C) 10cm
(D) 12 cm
20. किसी घन का किनारा एवं उसके विकर्ण की लम्बाई का अनुपात है
(A) √3 : 1
(B) 1 : 2
(C) √3 : 2
(D) 1 : √3
21. बिन्दु ( –5, 12) की मूल बिन्दु से दूरी कितनी होगी ?
(A) 7
(B) 13
(C) 17
(D) 5
22. बिन्दुओं ( – 2, 3) और (4, 1) को मिलाने वाले रेखाखण्ड के मध्य बिन्दु का नियामक है
(A) (1, 2)
(B) (− 1, 2)
(C) (1,−2)
(D) (2, 2)
23. cosec (90° – θ) • sin (90° – θ) किसके बराबर है ?
(A) 1
(B) –1
(C) 0
(D) 1/2
24. 1 + cot2 A / 1 + tan2 A बराबर है
(A) sin2A
(B) cos2A
(C) cot2A
(D) tan2A
25. निम्न में से कौन-सी अभाज्य संख्या है ?
(A) 29
(B) 25
(C) 16
(D) 15
26. एक 6 मीटर ऊँचे खंभे की छाया पृथ्वी पर 2√3 मी लम्बी है। सूर्य का उन्नयन कोण होगा
(A) 60°
(B) 45°
(C) 30°
(D) 15°
27. एक 14 सेमी ऊँचाई के बेलन के वक्र पृष्ठ का क्षेत्रफल 264 सेमी2 है। इसका आयतन (सेमी3) में है
(A) 296
(B) 369
(C) 396
(D) 503
28. एक बेलन और के आधार समान हैं। यदि उनकी ऊँचाइयाँ भी समान हों, तो उनके आयतनों का अनुपात होगा
(A) 1 : 2
(B) 2 : 3
(C) 3 : 2
(D) 3 : 1
29. y = 10 का आलेख कैसी सरल रेखा होगी ?
(A) x-अक्ष के सामांतर
(B) y-अक्ष के सामांतर
(C) मूल बिन्दु से जाती हुई
(D) इनमें से कोई नहीं
30. दो पासों को एक साथ फेंका जाता है। दोनों पासों पर अंक 5 आने की प्रायिकता होगी
(A) 1/2
(B) 1/36
(C) 1/6
(D) इनमें से कोई नहीं
31. 6 सेमी त्रिज्या वाले अर्द्धवृत्त की कुल परिमिति होगी
(A) (π + 1) 6cm
(B) (π + 2) 6cm
(C) (π + 36) 6cm
(D) 6π cm
32. 8cm त्रिज्या वाले वृत्त के अन्तः वर्ग का क्षेत्रफल है
(A) 64 cm2
(B) 100 cm2
(C) 125 cm2
(D) 128cm2
33. 2x + 3y = 5 का आलेख होता है
(A) वक्र रेखा
(B) सरल रेखा
(C) वृत्त
(D) इनमें से कोई नहीं
34. दो रैखिक समीकरणों के आलेख प्रतिच्छेदी रेखाएँ हैं, तब रैखिक समीकरण युग्म का
(A) कोई हल नहीं है
(B) एक हल है
(C) दो हल हैं
(D) अनेक हल हैं
35. p का मान जिसके लिए बहुपद x3 + 4x2 – px + 8 पूर्णतया (x – 2) से विभाज्य है
(A) 0
(B) 3
(C) 15
(D) 16
36. (3-√3)/1 हैं।
(A) परिमेय संख्या
(B) अपरिमेय संख्या
(C) पूर्णांक संख्या
(D) इनमें से कोई नहीं
37. दो परिमेय संख्याओं के बीच अधिकतम कितनी संख्याएँ हो सकती हैं ?
(A) 2
(B) 3
(C) 4
(D) अनन्त
38. सामांतर श्रेणी 6, 13, 20, ….216 का मध्य पद है
(A) 118
(B) 104
(C) 111
(D) 125
39. सामांतर श्रेणी 14, 9, 4, – 1, – 6,… का n वाँ पद है
(A) (19 + 5n)
(B) (19 – 5n)
(C) (19 + n)
(D) इनमें से कोई नहीं
40. द्विघात समीकरण ax2+ bx + c = 0, (a ≠ 0) में x के मान होंगे
(A) –b±√b2+ 4ac) / 2a
(B) –b±√4ac – b2 / 2a
(C) –b±√b2 – 4ac) / 2a
(D) b2 ± 4ac
41. y- अक्ष पर वह बिन्दु, जिसकी बिन्दु (4, 2) से दूरी 5 है, निम्नलिखित में से कौन है ?
(A) (1,0)
(B) (0, – 1)
(C) (2,-5)
(D) (3, 5)
42. मूल बिन्दु से बिन्दु P( –a, –b) की दूरी है
(A) √a2 + b2 इकाई,
(B) √a2 – b2 इकाई
(C) (a2 + b2) इकाई,
(D) (a + b) इकाई
43. आँकड़े 12, 17, 81, 26, 38, 42, 57, 62 का परिसर है
(A) 12
(B) 62
(C) 81
(D) 69
44. यदि एक वृत्त का क्षेत्रफल 154 cm2 है, तो इसकी परिधि है
(A) 22 cm
(B) 33 cm
(C) 44 cm
(D) 66 cm
45. बिन्दु ( –13, –18) का भुज है
(A) –12
(B) –13
(C) –18
(D) –31
46. किसी त्रिभुज के तीनों शीर्षों के निर्देशांक क्रमश: (4, 6), (7, 11) एवं (- 2, 4) है। इसके केन्द्रक का निर्देशांक है
(A) (7 , 3)
(B) (3 , 7)
(C) (11 , 4)
(D) ( 7 , – 4)
47. tan2 60° का मान है
(A) 1
(B) 3
(C) 1 / √3
(D) 1 / 3
48. sin2 22° + cos2 22° का मान है
(A) 1
(B) 2
(C) 1/2
(D) –1
49. संख्या 0.32 को P/q के रूप में (जहाँ, p, q पूर्णांक है, q ≠ 0) लिखा जा सकता है
(A) 8/25
(B) 29/90
(C) 32/99
(D) 32/199
50. निम्नलिखित में से कौन सा भिन्न का दशमलव प्रसार सांत है ?
(A) 11 / 700
(B) 91 / 2100
(C) 343 / 23x 53 x 73
(D) इनमें से कोई नहीं
51. यदि f (x) = 2x2 + 6x – 6 का शून्यक α, β है, तो
(A) α + β= αβ
(B) α + β = > αβ
(C) α + β < αβ
(D) α + β+ αβ = 0
52. सरल रेखाएँ x = -2 तथा y = 3 का कटान बिन्दु है
(A) (–2 , 3)
(B) (2 , – 3)
(C) (3 , – 2)
(D) (–3 , 2)
53. कार्तीय तल में स्थित किसी बिन्दु (3, 4) की कोटि का मान है
(A) – 4
(B) 3
(C) – 1
(D) – 7
54. यदि cosec θ = √10 हो, तो sec θ का मान होगा
(A) 3/√10
(B) √10/3
(C) 1/√10
(D) 2/√10
55. दी गई आकृति में BOC वृत्त का व्यास है तथा AB = AC है तो ∠ABC
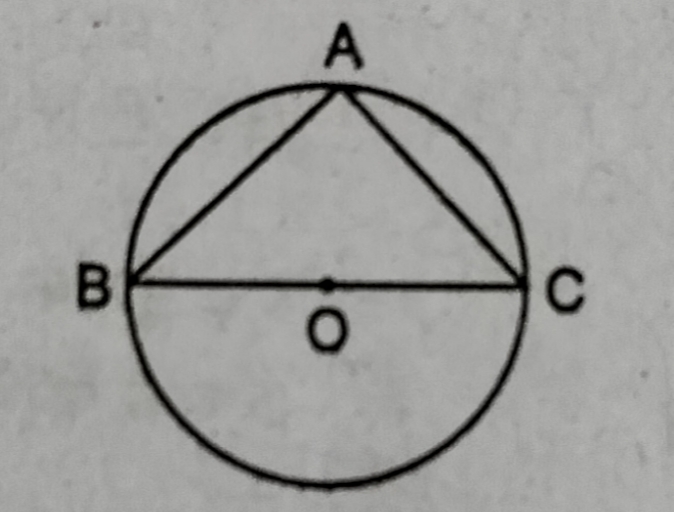
(A) 30°
(B) 60°
(C) 45°
(D) 90°
56. दी गई आकृति में यदि ABCD एक सामांतर चतुर्भुज है, तो ∠ACB की माप है
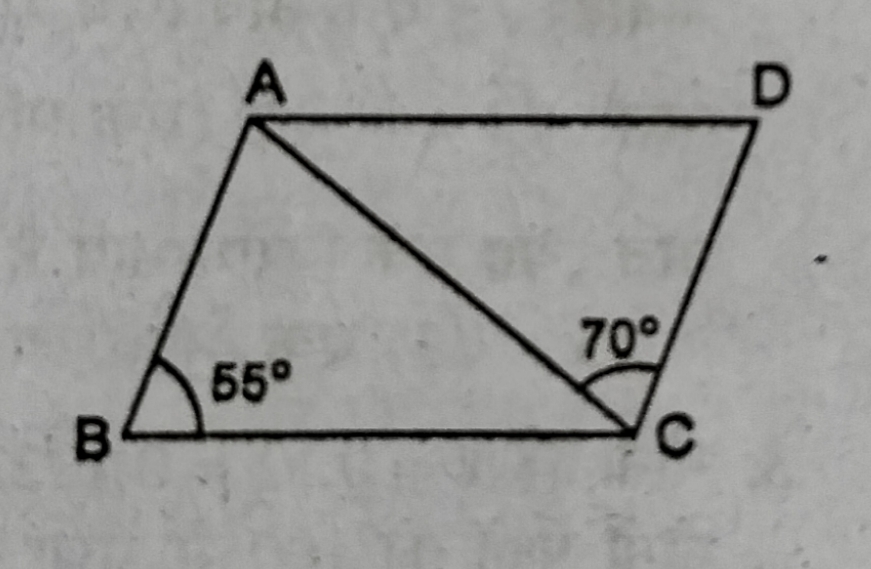
(A) 70°
(B) 55°
(C) 25°
(D) 125°
57. यदि समान्तर श्रेणी का सामान्य पद (5n – 7) है तो इसका प्रथम पद होगा
(A) 0
(B) –7
(C) 2
(D) –2
58. समान्तर श्रेणी 3, 7, 11, ….. का 14 वाँ पद है
(A) 52
(B) 55
(C) 56
(D) 59
59. यदि समीकरण 3x2 – 10x + 3 का एक मूल 1/3 है तो दूसरा मूल होगा
(A) -1/3
(B) 1/3
(C) -3
(D) 3
60. संख्या 2.13113 1113 11113 …. है
(A) पूर्णांक
(B) परिमेय संख्या
(C) अपरिमेय संख्या है
(D) इनमें से कोई नहीं।
प्रश्न- यूक्लिड विभाजन एल्गोरिथ्म के प्रयोग से 255 एवं 867 का म० स० निकालें।
उत्तर– 867 >255
मानलिया कि a = 867, b = 255
यूक्लिड विभाजन एल्गोरिथ्म के अनुसार,
a = bq + r
867 = 255 × 3+102
255=102 x 2 + 51
102 = 51 x 2 +0
यहाँ पर शेषफल शून्य है एवं अंतिम भाजक = 51 है।
∴ 255 एवं 867 का म०स० = 51
प्रश्न- सिद्ध करें कि (5 + √3) एक अपरिमेय संख्या है।
उत्तर– यदि संभव है तो मानलिया कि (5+ √3) एक परिमेय संख्या है।
∴ 5 + √3 = p/q (जहाँ p एवं q सह अभाज्य पूर्णांक है, और q ≠ 0)
∴ √3 = P / q -5
∴ p और q पूर्णांक है
∴ p/q – 5 एक परिमेय संख्या है,
जबकि √3 एक अपरिमेय संख्या है।
अतः √3 ≠ p / q – 5 (एक परिमेय संख्या ≠ एक अपरिमेय संख्या)
अतः यह एक विरोधाभाष है। इसलिए हमारी मान्यता गलत हुई ।
∴ (5 + √3) एक अपरिमेय संख्या होगी।
प्रश्न- 0.12 को P/q के रूप में लिखें
उत्तर– माना कि x = 0.12 = 0.22222…
दोनों पक्षों को 100 से गुणा करने पर,
100x = 12.222
फिर समीकरण (i) को 10 से गुणा करने पर,
1000x = 122.222
अब समीकरण (i) को समीकरण (ii) से घटाने पर,
900x = 110 ∴ x = 110/900 = 11/90 ⇒ 0.12=11/90; Ans
प्रश्न- यदि बहुपद ( x2– ax + a – 1) का एक गुणनखंड (x – a) है, तो ‘a’ का मान ज्ञात करें।
उत्तर– माना कि p(x) = x2 – ax + a – 1
चूकि (x – a), p(x) का एक गुणनखंड है, तब p(a) =0
⇒ a2 – a × a + a – 1 = 0
⇒ a2 – a2 + a – 1 = 0
⇒ a – 1 = 0 ∴ a = 1
प्रश्न- यदि द्विघात बहुपद (5x2 + 7x + 1) के शून्यक α एवं β हों तो (1/α + 1/β) का मान क्या होगा ?
उत्तर– 5x2 – 7x + 1
∴ α +β = -b/a = –(–7)/5 = 7/5; α · β = c/a = 1/5
अब 1/α + 1/β = α +β / αβ = 7/5/1/5 = 7/5 x 5/1 = 7;Ans
प्रश्न-समीकरण निकाय 6x + 5y = 11 एवं 9 x + 10 y = 21 को वज्रगुणन विधि से हल करें।
उत्तर– दिया गया है, 6x + 5y = 11, 9x + 10y = 21
⇒ 6x – 5y – 11 = 0, 9x + 10y – 21 = 0
अब वज्रगुणन विधि से,
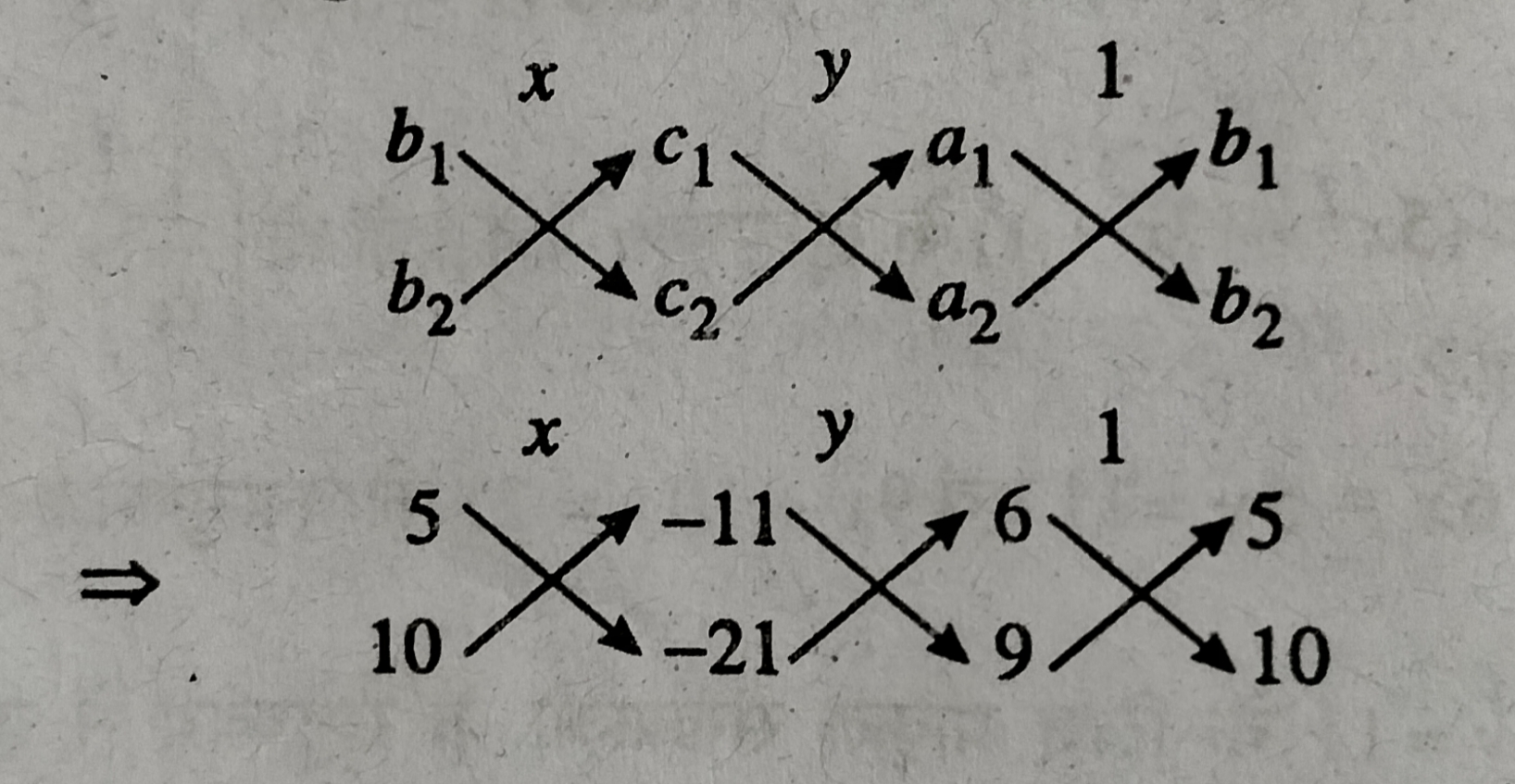
तब x / 5(–21) – 10(–11) = y / –11 x 9–(–21) x 6 = 1 / 6 x 10 – 9×5
या, x / –105+110 = y / –99+126= 1 / 60 – 45 या x / 5 = y / 27 = 1 / 15
अर्थात् x / 5 = 1/15 या x= 5 / 15 = 1 / 3
एवं y / 27 = 1 / 15 या y = 27 / 15 = 9 / 5
अतः x= 1 / 3, y=9 / 5; Ans.
प्रश्न- समीकरण 3x + y = 11 के लिए प्राकृत संख्याओं के समुच्चय में हल लिखें।
उत्तर– 3x + y = 11, या, y = 11 – 3x
यदि x = 1, y =11 – 3 ×1 = 8; (1, 8)
यदि x = 2, y = 11 – 3 × 2 = 5; (2,5)
यदि x = 3, y = 11 – 3 × 3 = 2; (3, 2)
यदि x = 4, y = 11 – 3 × 4 = −1; (4, −1)
अतः दिये गए समीकरण का प्राकृत संख्याओं के समुच्चय में हल
= (1, 8), (2, 5), (3, 2); Ans.
प्रश्न- द्विघात समीकरण 3x2 – 4x + 4 = 0 के मूलों की प्रकृति ज्ञात करें
उत्तर– दिया गया समीकरण— 3x2 – 4x – 1 = 0
समीकरण को ax2 + bx + c = 0 से तुलना करने पर हम पाते हैं कि
a = 3, b = –4, c = 4
∴ D = b2 – 4ac से D = (–4)2 – 4 x 3 x 4 = 16 – 48 = –32
अत: D < O
∴ दिये गए समीकरण के मूल काल्पनिक होंगे।
प्रश्न- द्विघात सूत्र का प्रयोग कर समीकरण 3x2 – 4x – 1 = 0 का हल निकालें।
उत्तर– दिया गया समीकरण है- 3x2 – 4x – 1 = 0
अतः a = 3, b = –4, c= –1(ax2 + bc + c का रूप तुलना करने पर)
अब D = b2 – 4ac = (–4)2 – 4 x 3 (–1) = 16 + 12 = 28 > 0
∴ D > 0
∴ x = -b ±√D / 2a = – (–4) ±√28 / 2 x 3
= 4 ± 2√7 / 6 = 4+2√7 / 6, 4–2√7 / 6 = 2+√7 / 3, 2–√7/3
अतः दिये गए समीकरण का हल = { 2+√7 / 3 , 2 – √7 / 3} Ans.
प्रश्न- यदि किसी सामांतर श्रेणी का 7वाँ पद 1/9 तथा 9 वाँ पद 1/7 है, तो 63वाँ पद का मान निकालें।
उत्तर– माना कि प्रथम पद ‘a’ तथा सर्वान्तर d है।
प्रश्नानुसार, a + (7 – 1)d =1 / 9 ⇒ a + 6d = 1/9
एवं a + (9–1)d = 1 / 7 ⇒ a + 8d = 1 / 7
समीकरण (ii) में से समीकरण (i) को घटाने पर,
(a + 8d) – (a + 6d) = 1/7 – 1/9
⇒ 2d = 9 – 7 / 63 = 2 / 63 ⇒ d = 2 / 63 x 1 / 2 = 1 / 63
अब समीकरण (i) में d का मान रखने पर,
a + 6 × 1 / 63 = 1 / 9 ⇒ a = 1 / 9 – 2 / 21 = 21 – 18 / 9 × 21 = 1 / 63
∴ Tn = a. + (n – 1)d
∴ T63 = 1/63 + (63 – 1) x 1 / 63 = 1 / 63 + 62 / 63 = 1 + 62 / 63 = 63 / 63= 1; Ans.
प्रश्न- दो अंकों वाली कितनी संख्याएँ 3 से विभाज्य है ?
उत्तर– 3 से विभाज्य दो अंकोंवाली संख्याएँ हैं—
12, 15, 18, …, 99
यहाँ पर, a = 12, d = 3, l= 99, n= ?
∴ l = a + (n – 1) d ⇒ 99 = 12 + (n – 1)3
∴ n – 1 = 99 – 12 / 3 = 87 / 3 = 29
∴ n = 29 + 1 = 30
अतः 3 से विभाज्य दो अंकों की कुल संख्याएँ = 30; Ans.
प्रश्न- ΔABC में DE || BC है और AD/DB = 3/5 है। यदि AC =4.8cm हो, तो AE की लम्बाई क्या होगी ?
उत्तर–
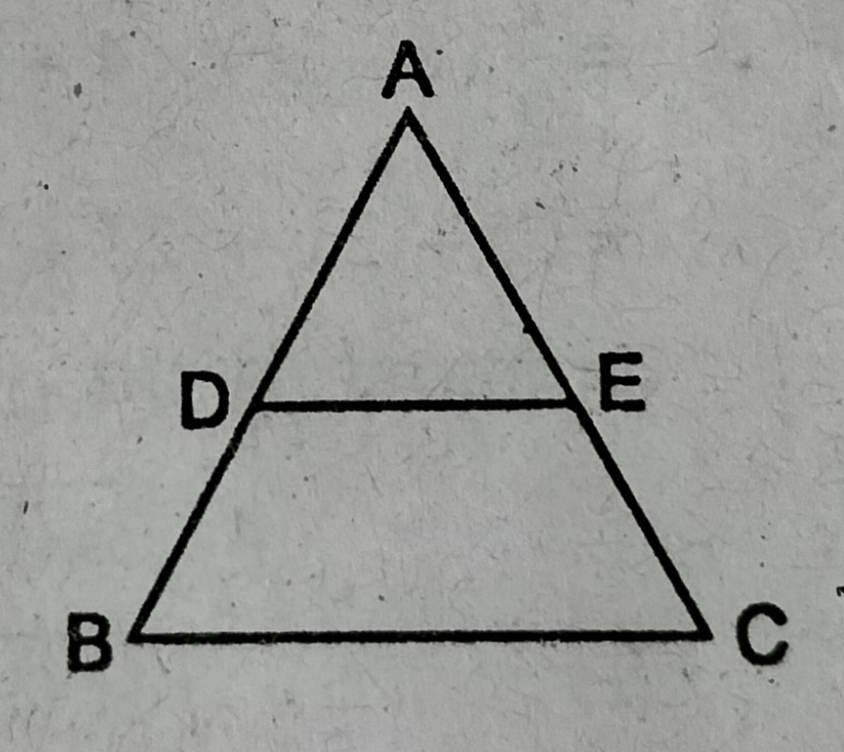
चूँकि त्रिभुज ABC में DE || BC है।
∴ थेल्स प्रमेय से, AD/DB = AE/EC
⇒ 3/5 = AE / AC – AE = 3/5 = AE / 4.8 – AE
⇒ 14.4 – 3AE = 5AE
⇒ 14.4 = 8AE ∴ AE = 14.4 / 8 = 1.8
∴ AE = 1.8cm Ans.
प्रश्न- दी गई आकृति में ΔAOD ~ ΔCOB तो सिद्ध करें कि AD॥ BC है।
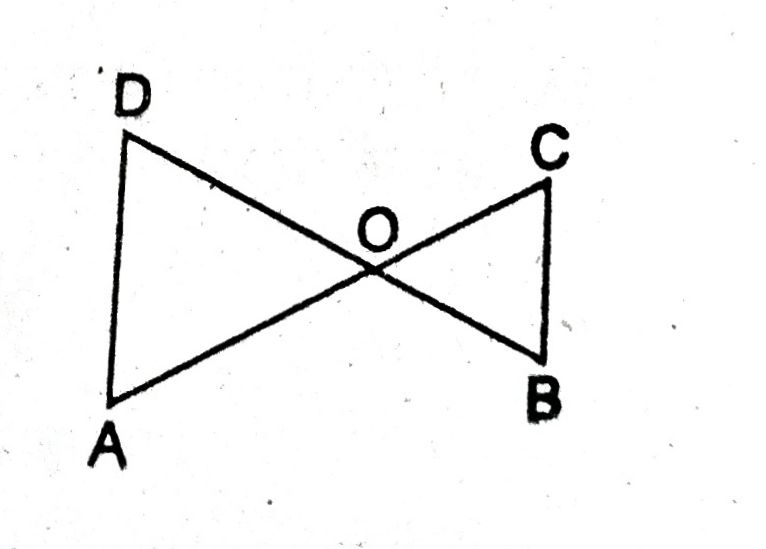
उत्तर– दिया है— ΔAOD ~ ΔCOB
∴ ∠A =∠C
∠D = ∠B
एवं AOD = COB
(शीर्षाभिमुख कोण)
:: A = C
जो कि एकान्तर कोणों का एक युग्म है।
:: AD || BC होगा ।
प्रश्न- दो सकेन्द्रीय वृत्तों की त्रिज्याएँ 5cm और 3 cm हैं। बड़े वृत्त की उस जीवा की लम्बाई ज्ञात करें, जो छोटे वृत्त को स्पर्श करती है।
उत्तर–
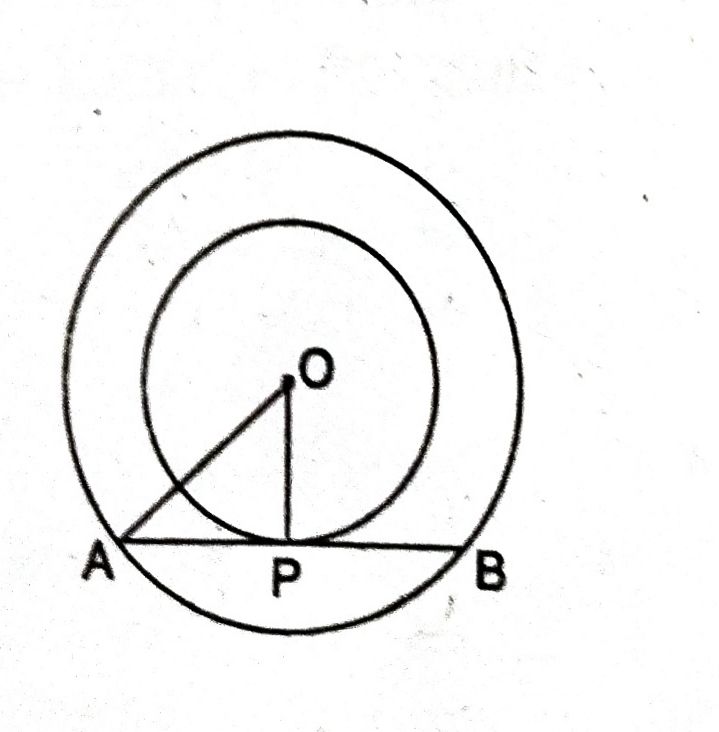
माना कि ‘O’ दो सकेन्द्रीय वृत्तों का केन्द्र है।
तथा OP = 3 cm एवं OA = 5cm बड़े वृत्त की जीवा AB, छोटे वृत्त के P बिन्दु पर स्पर्श रेखा है, तो हमें AB ज्ञात करना है।
चूँकि AB, P बिन्दु पर छोटे वृत्त की स्पर्श रेखा है।
∴ OP ⊥ LAB
फिर, चूँकि AB, बड़े वृत्त की जीवा है तथा केन्द्र 0 से OP LAB.
∴ P, AB का मध्य बिन्दु होगा।
अंतः AP = PB, या AB = 2AP
अब समकोण MOP में, AP2 = OA2 – OP2 = 52 -32
= AP2 = 25 – 9 = 16 ∴ AP = 4
∴ AB = 2AP=2 × 4 =8cm; Ans.
प्रश्न- cot2 45° + cosec2 30° + sec2 60° sin2 90° का मान ज्ञात करें।
उत्तर– cot245° + cosec230° + sec260° – sin290°
= (1)2 + (2)2 + (2)2 – (1)2
= 1 + 4 + 4 – 1 = 9 – 1 = 8 Ans
प्रश्न- सिद्ध करें कि √1 – cos A / √ 1 + cos A = cosecA – cotA
उत्तर– L.H.S = √ 1 – cos A / √ 1 + coa A = √ (1– cos A) (1 – cos A) / √(1 + cos A) (1 – cos A)
अंश एवं हर में (1 – cosA) से गुणा करने पर,
= √(1– cos A)2 / 1 – cos2A = √(1 – cosA)2 / sin2A
= 1 – cos A / sin A = 1 sin A – cos A / sin A
= cosec A – cot A = R.H.S ; Proved Ans.
प्रश्न- एक बक्से में 4 लाल एवं 6 काली गेंदें हैं। बक्से में से एक गेंद यादृच्छया निकाला जाता है, तो इसके काले गेंद होने की प्रायिकता ज्ञात करें।
उत्तर– कुल गेंदे = 4 + 6 = 10, काली गेंदों की संख्या = 6 काली गेंद निकालने की प्रायिकता = P(A)
P(A) = 6/10 = 3/5 Ans
प्रश्न- दो पासों को एक बार फेंका जाता है, तो दोनों पासों की संख्या का योग आने की प्रायिकता ज्ञात करें।
उत्तर– यदि दो पासों को एक बार फेंका जाता है, तो कुल संभावनाएँ इस प्रकार हैं—
(1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6)
(2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6)
(3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6)
(4, 1) (4, 2) (4,3) (4, 4) (4, 5) (4, 6)
(5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6)
(6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6)
अब ऊपर से हम यह देख सकते हैं कि दो पासों के ऊपर संख्याओं का योग 8 आने की संभावनाएँ हैं—
(2, 6), (3, 5), (4 , 4), (5, 3), (6 , 2) = 5
अतः P (दोनों पासों पर अंकों योग 8) = 5/36 Ans.
प्रश्न- दूरी सूत्र का प्रयोग कर दर्शाइए कि बिन्दुएँ (-2, 5), (0, 1) तथा (2, 3 ) सरेखी है।
उत्तर– माना कि बिन्दुएँ A (-2, 5), B (0, 1) तथा C (2, 3) है।
अब दूरी सूत्र के अनुसार,
AB = √(–2 – 0)2 + (5 – 1)2 = √4 + 16 √20 =2√5
BC = √(0 – 2)2 + (1 + 3)2 = √4 + 16 = √20 = 2√5
CA = √[2 – (–2)]2 + (–3–5)2 = √16 + 64 = √80 = 4√5
∴ AB + BC = 2√5 + 2√5 = 4√5 एवं CA = 4√5
∴ AB + BC = CA
अतः यह तभी संभव है जब बिन्दु A, B एवं C सरेख हैं।
प्रश्न- यदि बिन्दु (x, y), बिन्दुओं (6, -1) और (2, 3) से समदूरस्थ है, तो सिद्ध करें कि x – y = 3.
उत्तर– प्रश्नानुसार बिन्दु A समदूरस्थ है B एवं C से ।
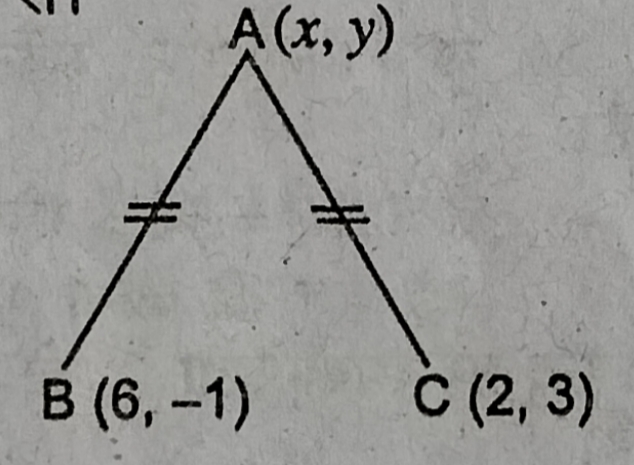
∴ AB = AC
⇒ AB2 = AC2
⇒ (x – 6)2 + (y + 1)2
=(x – 2)2 + (y – 3)2
⇒ x2 – 12x + 36 + y2+ 2y + 1
= x2 – 4x + 4 + y2 – 6y + 9
⇒ –12x + 2y + 37 = –4x – 6y + 13
⇒ –12x + 2y + 4x + 6y = 13 – 37
⇒ –8x + 8y = –24 = –(8x – 8y) = –24
⇒ –8(x – y)= –8 x 3= x – y = 3; Proved
प्रश्न- किसी बेलन के वक्रपृष्ट का क्षेत्रफल 1760 cm2 है एवं इसके आधार की त्रिज्या 14cm है। बेलन की ऊँचाई क्या होगी ?
उत्तर– बेलन के वक्र पृष्ठ का क्षेत्रफल = 1760 cm2
तथा आधार की त्रिज्या = 14cm
बेलन की ऊँचाई = ?
∴ बेलन के वक्र पृष्ठ का क्षेत्रफल = 1760 cm2
⇒ 2πrh = 1760
⇒ 2 x 22/7 x 14 x h = 1760 ∴ h = 7 x 1760 / 2 x 22 x 14 = 20cm
बेलन की ऊँचाई = 20cm; Ans.
प्रश्न- किसी शंकु के आधार की त्रिज्या 7cm है एवं इसकी उँचाई 14cm है, तो इसके वक्रपृष्ट का क्षेत्रफल ज्ञात करें।
उत्तर– शंकु के आधार की त्रिज्या (r) = 7 cm
शंकु की ऊँचाई (h) = 14 cm
शंकु की तिरछी ऊँचाई ( l ) = √r2 + H2
= √72 + 142 = √49 + 196
= √245 = 15.65
शंकु के वक्र पृष्ट का क्षेत्रफल = πrl
= 22 / 7 x 7 x 15.65
= 2410.1 / 7 = 344.3 cm2
प्रश्न- एक बिन्दु A से जो वृत्त के केन्द्र 0 से 5cm की दूरी पर है । वृत्त पर स्पर्श रेखा AT की लम्बाई 3cm है, तो वृत्त की त्रिज्या OT की लम्बाई क्या होगी ?
उत्तर–
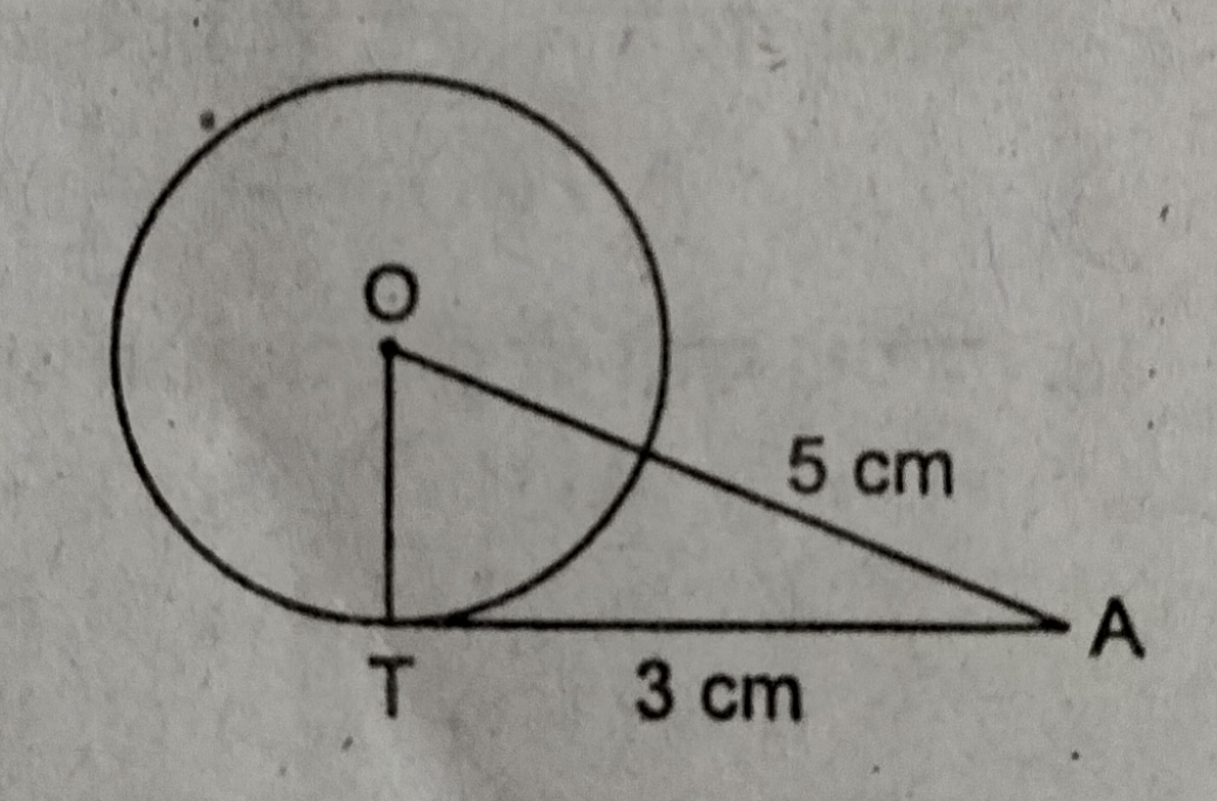
पाइथागोरस प्रमेय के अनुसार,
OA2 = OT2 + AT2
⇒ 52 = OT2+ 32
⇒ 25 = OT2 + 9
⇒ OT2 = 25 – 9 = 16
∴ OT = 4m
∴ वृत्त की त्रिज्या = 4cm; Ans
प्रश्न- एक अर्द्धवृत्ताकार पार्क का क्षेत्रफल ज्ञात करें जिसका परिमाप 360m है।
उत्तर– दिया गया है— अर्द्धवृत्ताकार पार्क की परिमाप = 360m
⇒ πr + 2r = 360 ⇒ r(π + 2) = 360
⇒ r( 22/7 + 2) = 360 ⇒ r x 36/7 = 360
∴ r = 7 x 360 / 36 = 79cm
∴ पार्क का क्षेत्रफल = 1/2πr2 = 1/2 x 22/7 x 70 x 70 = 7700cm2 Ans
प्रश्न- निम्नलिखित बंटन का माध्य ज्ञात करें।
| वर्ग-अंतराल | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| बारंबारता | 20 | 24 | 40 | 36 | 20 |
उत्तर–
| वर्ग अंतराल | बारंबारता ( fi ) | वर्ग चिह्न ( xi ) | fi xi |
| 0 – 10 | 20 | 5 | 100 |
| 10 – 20 | 24 | 15 | 360 |
| 20 – 30 | 40 | 25 | 1000 |
| 30 – 40 | 36 | 35 | 1260 |
| 40 – 50 | 20 | 45 | 900 |
| ∑fi = 140 | ∑fi xi = 3620 |
माध्य = ∑fi xi / ∑fi = 3620 / 140 = 25.857 = 25.86; Ans.
प्रश्न- दो अंकों की एक संख्या अपने अंकों के जोड़ की चार गुनी है एवं अपने अंकों के गुणनफल की दोगुनी है। संख्या ज्ञात करें।
उत्तर– माना कि दहाई का अंक x तथा इकाई का अंक y है।
अतः उन अंकों से बनी संख्या = 10x + y
प्रश्नानुसार, 10x + y = 4 (x + y)
⇒ 10x + y = 4x + 4y ⇒10x – 4x = 4y – y
⇒ 6x = 3y ⇒ 2x = y
तथा पुनः 10x + 2x = 2x × 2x
⇒ 10x + 2x = 2x × 2x
⇒ 12x = 4x2 ⇒ x = 3
फिर y = 2x = 2 × 3 = 6
अतः अभीष्ट संख्या = 10x + y =10 × 3 + 6 = 36; Ans.
प्रश्न- एक त्रिभुज ABC के अन्तः वृत्त की त्रिज्या 4 सेमी है तथा उन दो रेखा खण्डों BD तथा DC की लम्बाइयाँ, जिनसे भुजा BC, स्पर्श बिन्दु D द्वारा विभाजित होती है, 6cm तथा 8 cm है। भुजाओं AB तथा AC की लम्बाइयाँ ज्ञात करें।
उत्तर– ΔABC के अन्त: वृत्त की त्रिज्या
(OD) = 4 cm, BD = 6cm, DC = 8cm,
जिनमें भुजा BC स्पर्श बिन्दु D द्वारा विभाजित होती है।
AB एवं AC की लम्बाई ज्ञात करनी है।
चूँकि किसी बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं की लम्बाई से समान होती है।
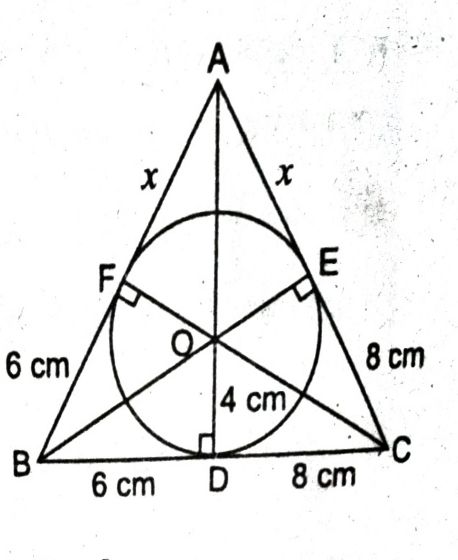
∴ AE = AF = x (माना)
BD = BF = 6cm तथा CD = CE = 8cm
∴ AB = 6 + x, AC = 8 + x
ABC में, s = AB + BC + AC / 2 = 6 + x + 14 + 8 + x / 2 = 28 + 2x / 2 = 14 + x
ABC का क्षेत्रफल = √s(s – a) (s – b) (s – c)
= √(14 + x) (14 + x – 6 – x) (14 + x – 14) (14 + x – 8 – x)
= √(14 + x) X 8 X x X 6 = √ 48x(14 + x)
= 4√3x (14 + x)
अब OA, OB, OC, OE एवं OF को मिलाया।
अतः ΔABC का क्षेत्रफल
= ΔAOB का क्षेत्रफल + BOC का क्षेत्रफल + AOC का क्षेत्रफल
= 1/2 (6 + x) x 4 + 1/2 x 14 x 4 + 1/2 (8 + x) x 4
= 12 + 2x + 28 + 16 + 2x = 4x + 56 = 4(x + 14)
समीकरण (i) एवं (ii) से,
4√3x(14 + x) = 4(x + 14)
⇒ √3x(14 + x) = (x + 14)
दोनों ओर वर्ग करने पर,
3x(14 + x) = (x + 14) (x + 14)
⇒ 3x = x + 14 = 2x = 14, ∴ x = 7
अत: AB = 6 + x = 6 + 7 = 13cm;
AC = 8 + x = 8 + 7 = 15cm; Ans
प्रश्न- एक खिलौना 3.5cm त्रिज्या वाले शंकु के आकार का है, जो इसी त्रिज्या वाले गोलार्द्ध के ऊपर है। खिलौने की कुल ऊँचाई 15.5cm है। खिलौने का क्षेत्रफल ज्ञात करें।
उत्तर– खिलौने की कुल ऊँचाई = 15.5cm
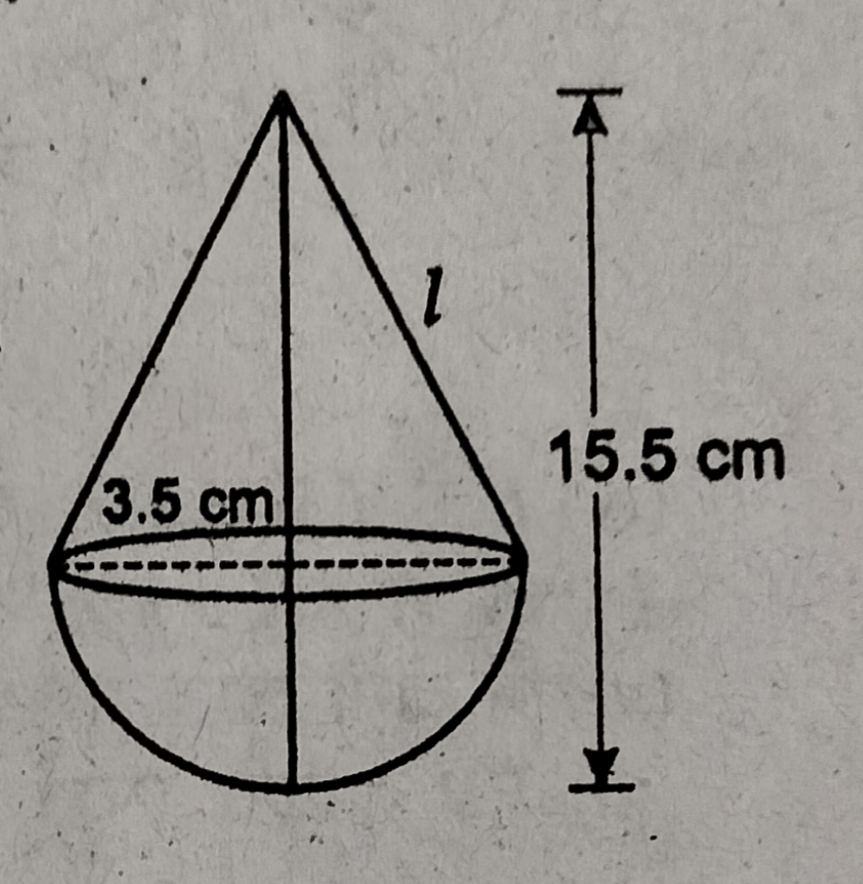
त्रिज्या = 3.5cm
∴ शंकु की ऊँचाई (h) = (15.5 – 3.5) cm = 12cm
शंकु की तिर्यक ऊँचाई ( I )
=√h2 + r2
= √122 + (3.5)2
= √144 + 12.25 = √156.25 = 12.5cm
खिलौने का कुल पृष्टीय क्षेत्रफल
= अर्द्धगोले के वक्र पृष्ट का क्षेत्रफल + शंकु के वक्र पृष्ट का क्षेत्रफल
= 2πr2 + πr(2r + l)
= 22/7 x 3.5(2 x 3.5 + 12.5)
= 11(7 + 12.5) = 11 x 19.5 = 214.5cm2 Ans
प्रश्न- सिद्ध करें कि यदि एक रेखा किसी त्रिभुज की किन्हीं दो भुजाओं को एक ही अनुपात में विभाजित करती है, तो वह रेखा तीसरी भुजा के सामांतर होती है।
उत्तर– विशेष प्रतिज्ञा – मान लिया कि DE, ABC की भुजा AB तथा AC से क्रमश: D तथा E पर इस प्रकार मिलती है
कि AD/DB = AE/EC
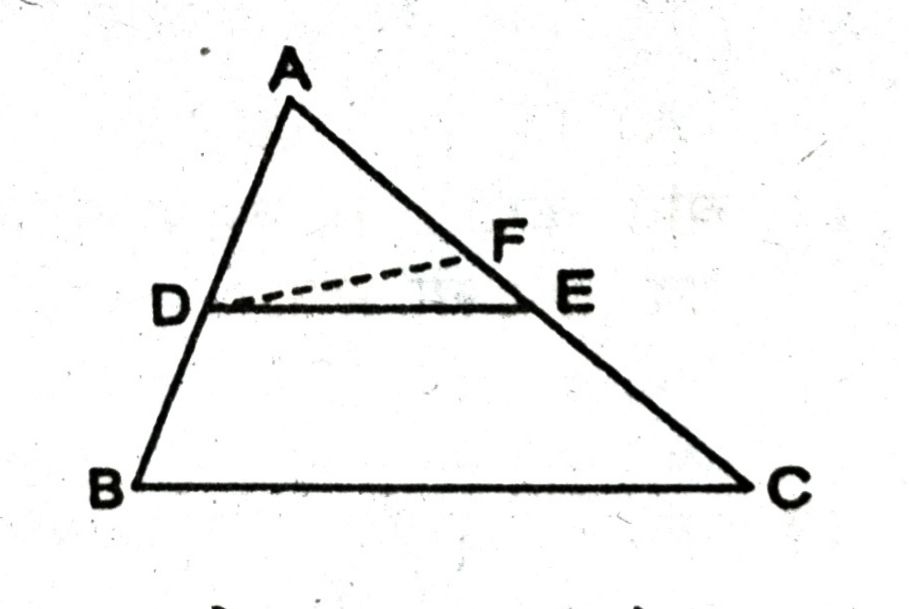
सिद्ध करना है— DE || BC
रचना—यदि संभव हो तो माना कि DE, BC के सामान्तर नहीं है। अतः D से BC के सामान्तर DF खींचा जो AC से F पर मिलती है।
प्रमाण— ΔABC में, DF || BC (रचना से) (थेल्स प्रमेय से)
∴ AD/DB=AF/FC
किन्तु दिया गया है कि AD/DB = AE/EC
∴ AE/EC = AF/FC
⇒ AE/EC+1 = AF/FC+1 (दोनों ओर 1 जोड़ने पर)
⇒ AE + EC / EC = AF + FC / FC
⇒ AC/EC = AC/FC = 1/EC = 1/FC
⇒ EC = FC
यह तभी संभव है जब बिन्दु F, बिन्दु E को ढँक ले।
तब DE || BC होगा (क्योंकि DF || BC है।)
प्रश्न- सिद्ध करें कि tan 0 / 1- cot 0 + cot 0 / 1- tan 0 = 1+tan 0 + cot 0
उत्तर– L.H.S= tanθ / 1 – cotθ + cot θ / 1 – tanθ = tanθ / 1 / 1 – tanθ + 1 / tanθ / 1 – tanθ
= tan2θ / tanθ – 1 + 1 / tanθ (1 – tanθ)
= tan2θ / tanθ – 1 + 1 / tanθ (tanθ – 1)
= tan3θ – 1 / tanθ (tanθ – 1) = (tanθ – 1) (tan2θ + tanθ + 1) / tanθ (tanθ – 1
= tan2θ + tanθ + 1 / tanθ = tan2θ / tanθ + tanθ / tanθ + 1 / tanθ
= tanθ + 1 + cotθ = 1 + tanθ + cotθ= R.H.S; proved.
प्रश्न- समीकरण युग्म 3x – y = 2 तथा 9x – 3y = 6 का ग्राफ खींचें और हल करें।
उत्तर– समीकरण युग्मं है— 3x – y = 2
9x – 3y = 6
समीकरण (i) से, 3x – y = 2 ⇒ y = 3x – 2
| x | 1 | 2 | –1 |
| y | -2 | 4 | -5 |
फिर समीकरण (ii) से, 9x – 3y = 6 ⇒ 9x – 6 = 3y
⇒ y = 9x – 6 / 3 = 3(3x – 2)/3 ⇒ y = 3x – 2
| x | 1 | 2 | 0 |
| y | 1 | 4 | -2 |
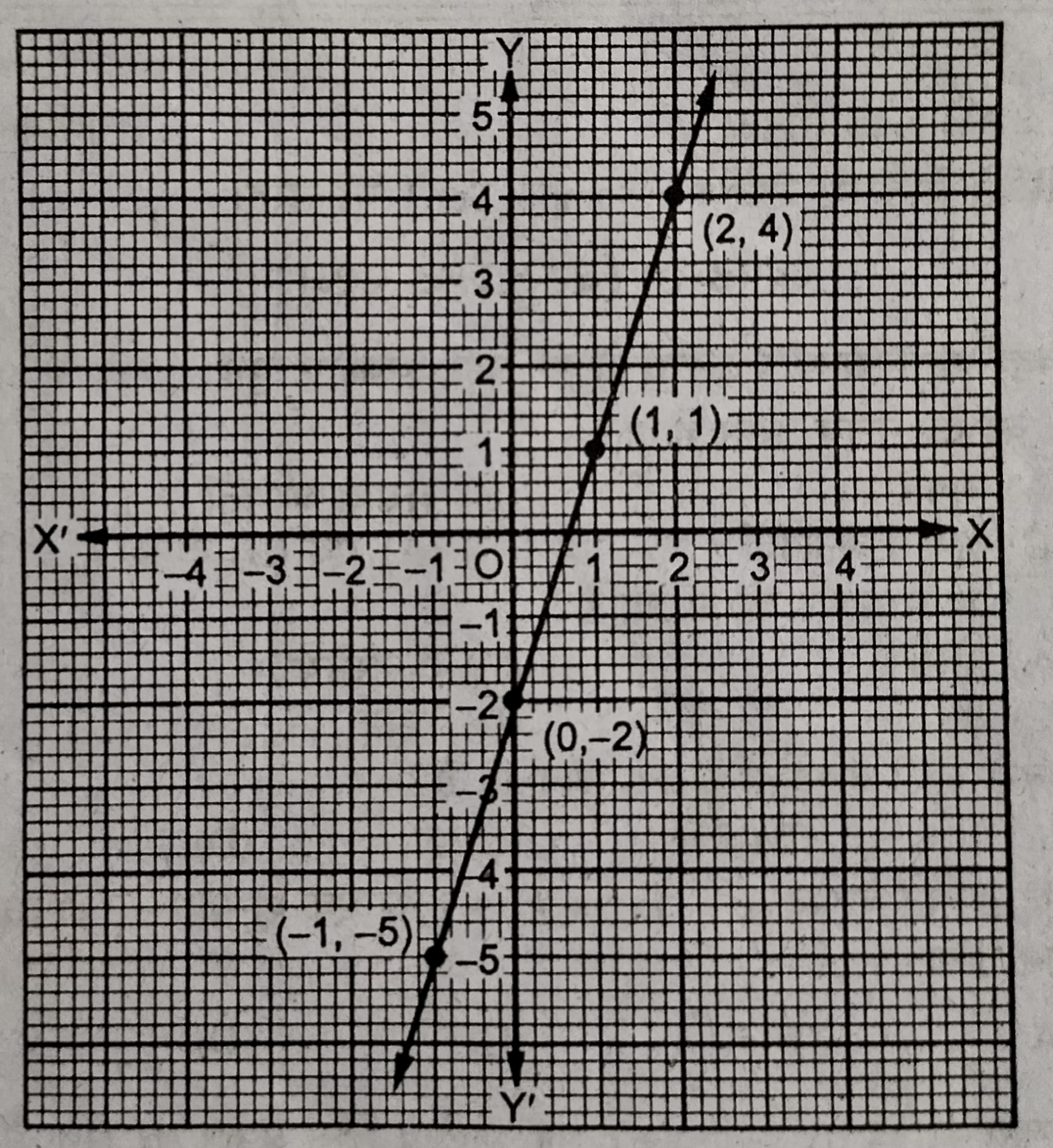
हम पाते हैं कि दोनों समीकरणों के ग्राफ AB एवं CD एक दूसरे के संपाती । अतः AB एवं CD पर स्थित सभी बिन्दु दोनों समीकरणों को संतुष्ट करते हैं। अतः दिये गए समीकरणों के निकाय के अनन्त हल होंगे।
प्रश्न- एक 60 मीटर चौड़ी सड़क के दोनों ओर आमने-सामने समान लम्बाई वाले दो खम्भे लगे हुए हैं। इन दोनों खंभों के बीच सड़क के एक बिन्दु से खंभों के शिखर के उन्नयन कोण 30° और 60° है। खंभों की ऊँचाई और खंभों से बिन्दु की दूरी ज्ञात करें।
उत्तर–
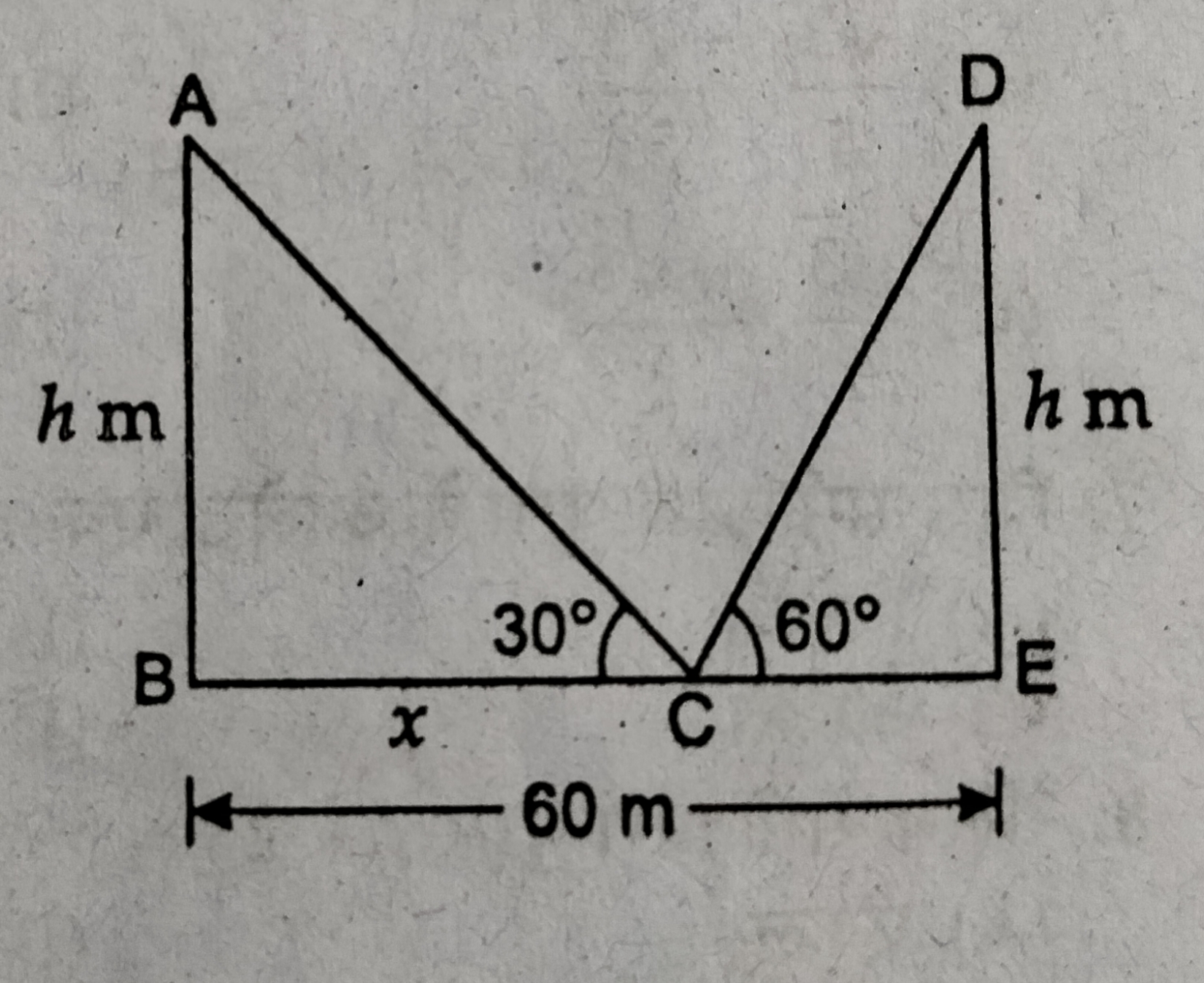
प्रश्नानुसार, दोनों खंभों के
बीच की दूरी = 60m
माना कि BC = x m
एवं CE = ( 60 – x ) m
AB = DE = खंभे की
ऊँचाई = hm
ABC में, tan 30° = h/x
= 1 / √3 = h / x
∴ x = √3h
अब ΔDCE में, tan 60° = h / 60 – x ⇒ √3 = h / 60 – x
⇒ 60√3 – √3x = h
⇒ 60√3 – √3 x √3h = h
⇒ 60√3 – 3h = h
⇒ 60√3 = 4h
∴ h = 15√3m
समीकरण (ii) से h का मान समीकरण (i) में रखने पर,
x = √3h = √3 ×15√3 = 45m
अतः खंभे की ऊँचाई = h = 15√3m
खंभे AB की C से दूरी = x = 45m
तथा खंभे DE की C से दूरी = 60 – x = 60-45 = 15 m; Ans.
प्रश्न- 4 सेमी त्रिज्या के एक वृत्त पर एक स्पर्श रेखा युग्म खींचें जो परस्पर 60° का कोण बनाता है।
उत्तर– रचना के चरण—
(i) O केन्द्र लेकर 4 cm त्रिज्या का एक वृत्त खींचा
(ii) कोई भी व्यास AOC खींचा।
(iii) त्रिज्या OL इस प्रकार खींचा कि ∠COL = 60° हो ।
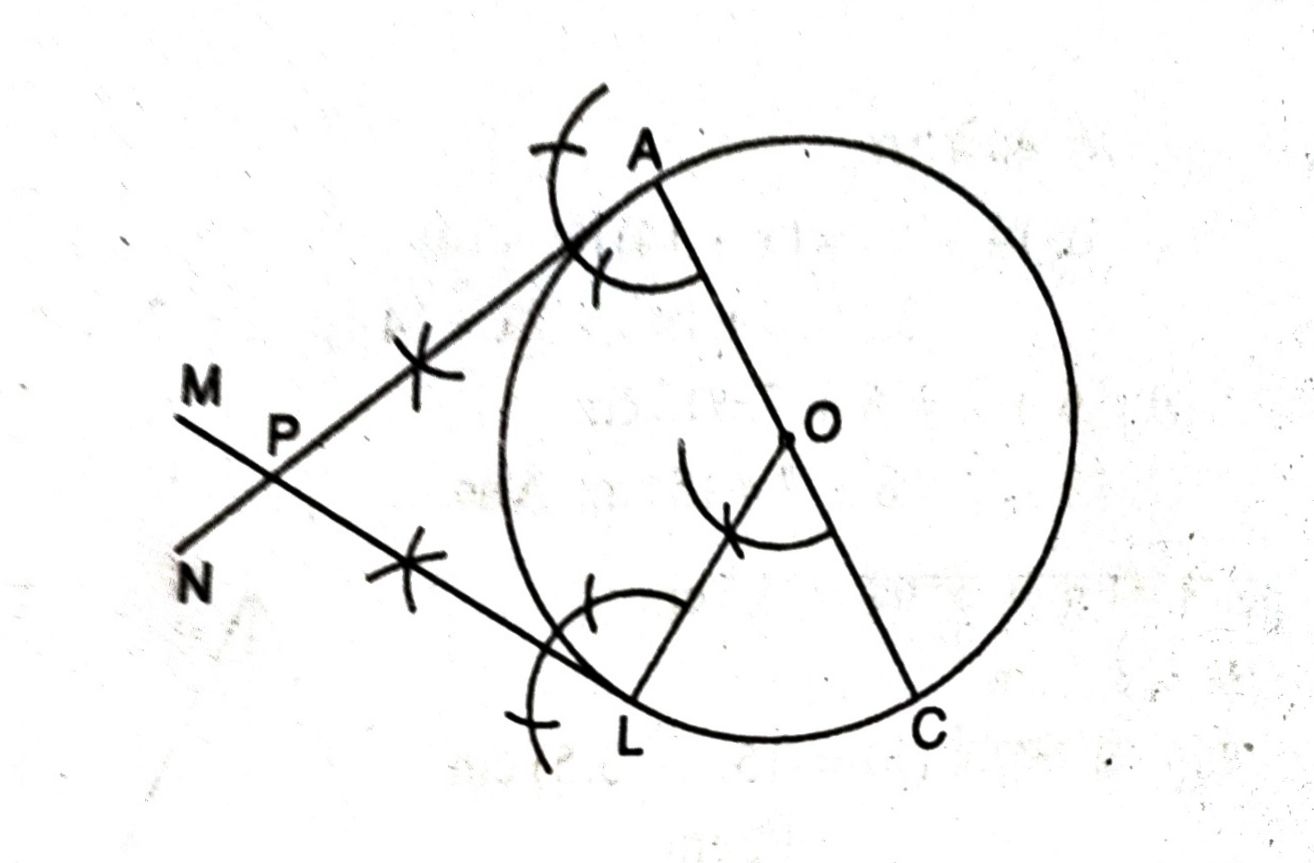
(iv) L से LM ⊥ OL खींचा।
(v) A से AN ⊥ OA खींचा
(vi) ये दोनों लम्ब परस्पर P बिन्दु पर प्रतिच्छेद करते हैं। तब PA एवं PB वांछित स्पर्श रेखाएँ होंगी।
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here