Bihar Secondary School Sample Paper Solved | BSEB Class 10th Sample Sets with Answers | Bihar Board class 10th Sample Paper Solved | Bihar Board Class 10th mathematics Sample set – 3
Bihar Secondary School Sample Paper Solved | BSEB Class 10th Sample Sets with Answers | Bihar Board class 10th Sample Paper Solved | Bihar Board Class 10th mathematics Sample set – 3
1. निम्नलिखित में से कौन सा भिन्न का दशमलव प्रसार सांत है ?
(A) 11 / 700
(B) 91 / 2100
(C) 343 / 23 x 53 x 73
(D) इनमें से कोई नहीं
2. वह कौन-सी छोटी से छोटी पूर्ण वर्ग संख्या है जो 16, 20 एवं 24 प्रत्येक से विभाज्य है ?
(A) 1600
(B) 2400
(C) 240
(D) 3600
3. यदि द्विघात समीकरण ax2 – 4ax + 2a + 1 = 0 के मूल समान हों, तो ‘a’ का मान होगा
(A) 0
(B) 1/2
(C) 2
(D) (A) एवं (B) दोनों
4. यदि 0.3x – 0.37 = 0.37x – 0.3 हो तो x का मान है
(A) -1
(B) -2
(C) 1
(D) 2
5. बहुपद x2 + 3x + 2 के शून्यक हैं
(A) -1, -2
(B) 2, -2
(C) -1, 2
(D) 1, -2
6. यदि p तथा q दो अभाज्य संख्याएँ हों तो उनका म०स० होगा
(A) 2
(B) 0
(C) 1 या 2
(D) 1
7. सामान्तर श्रेणी 2, 6, 10, 14,…. का कौन सा पद 82 है।
(A) 15वाँ
(B) 20वाँ
(C) 21 वाँ
(D) 22वाँ
8. यदि समीकरण kx – 5y = 2 तथा 6x + 2y = 7 का कोई हल नहीं हो तो
(A) k = -10
(B) k = -5
(C) k = -6
(D) k = -15
9. समबाहु ΔABC की एक भुजा 2a है, तो इसकी ऊँचाई है
(A) 3a
(B) √3a
(C) √3a2
(D) √3/2a
10. x, x + 3, x + 6, x + 9 तथा x + 12 का समान्तर माध्य है
(A) x + 6
(B) x + 5
(C) x + 7
(D) x + 8
11. दो चर में दो एक घातीय समीकरणों के ग्राफ यदि प्रतिच्छेदी रेखाएँ हों, तो हलों की संख्या है
(A) सिर्फ एक
(B) कोई हल नहीं
(C) अनन्त हल
(D) इनमें से कोई नहीं
12. किसी वृत्त के केन्द्र से 13 सेमी दूर स्थित बिन्दु P से खींची गई स्पर्श रेखा की लम्बाई 12 सेमी है, तो वृत्त की त्रिज्या है
(A) 6cm
(B) 12cm
(C) 9cm
(D) 5cm
13.6 सेमी भुजा वाले घन में से 2 सेमी भुजा वाले कितने घन बनाये जा सकते है ?
(A) 56
(B) 54
(C) 28
(D) 27
14. यदि (p + 1), (2p + 1), (4p – 1) A.P. में हैं तो p का मान है
(A) 1
(B) 2
(C) 3
(D) 4
15. निम्न में से कौन cos θ के बराबर है ?
(A) √sin2 θ – 1
(B) √1 – sin2θ
(C) √1 + sin2 θ
(D) √1 – cos2 θ
16. यदि 15cotA = 8 हो, तो sin A का मान होगा
(A) 15/17
(B) 17/15
(C) 15/8
(D) 8/17
17. sec2 60° -1 का मान है
(A) 2
(B) 3
(C) 4
(D) 0
18. यदि 3 cosθ = 2 हो, तो ( 2sec2θ + 2 tan2θ – 7) का मान होगा
(A) 0
(B) 1
(C) 3
(D) 4
19. किसी घटना E के घटित होने की प्रायिकता P(E) हो, तो निम्नलिखित में कौन सही है ?
(A) P(E) < 0
(B) P(E) > 1
(C) -1≤ P(E) ≤ 1
(D) 0 ≤ P(E) ≤ 1
20. दो संख्याओं का गुणनफल 8670 है और उसका म०स० 17 है, तो उसका ल०स० होगा
(A) 102
(B) 85
(C) 107
(D) 510
21. एक घड़ी की मिनट की सुई 21 cm लम्बी है। इसके द्वारा 10 मिनट में रचित क्षेत्रफल है
(A) 126 cm2
(B) 210cm2
(C) 231cm2
(D) 252cm2
22. प्रथम पाद में स्थित किसी बिन्दु की x- अक्ष की दूरी क्या कहलाती है ?
(A) भुज
(B) कोटि
(C) (A) और (B) दोनों
(D) इनमें से कोई नहीं
23. यदिR (5,6) बिन्दुओं A(6,5) एवं B(4,y) को मिलानेवाली रेखाखंड AB का मध्य बिन्दु है तो y का मान होगा
(A) 5
(B) 7
(C) 12
(D) 6
24. बिन्दुओं (9, 3) एवं ( 15, 11) के बीच की दूरी है ?
(A) 11
(B) 10
(C) 13
(D) 6 (D) 12
25. ΔPQR में यदि PQ2 = PR2 + QR2 हो तो त्रिभुज का कौन-सा कोण समकोण होगा?
(A) ∠P
(B) ∠Q
(C) ∠R
(D) इनमें से कोई नहीं
26. ΔABC में DE || BC इस प्रकार है कि AD/ DB = 3/5 ! यदि AC = 5.6cm तब AE का मान होगा
(A) 4.2cm
(B) 3.1cm
(C) 2.8cm
(D) 2.1cm
27. दो खंभे 13 मी और 7 मी ऊँचे हैं और समतल जमीन पर ऊर्ध्वाधर खड़े हैं। यदि उनके पादों के बीच की दूरी 8m है तो उनके सिरों के बीच की दूरी है
(A) 10m
(B) 9m
(C) 12m
(D) 11m
28. यदि चार लगातार विषम संख्याओं का माध्य 6 है तो, सबसे बड़ी संख्या क्या है ?
(A) 5
(B) 9
(C) 21
(D) 15
29. यदि किसी बारंबारता सारिणी का माध्य 27 एवं माध्यिका 33 हो, तो बहुलक का मान होगा
(A) 30
(B) 43
(C) 45
(D) 47
30. दो सिक्कों की युगल उछाल में एक भी शीर्ष नहीं आने की प्रायिकता है
(A) 1/2
(B) 1/4
(C) 3/4
(D) 1
31. दो पासे एक साथ उछाले गये तो दोनों पर एक ही संख्या आने की प्रायिकता होगी है
(A) 1/2
(B) 1/3
(C) 1/6
(D) 1/12
32. ‘r’ त्रिज्या वाले गोला का आयतन होगा
(A) 4/3 πr3 घन इकाई
(B) 1/3 πr3 घन इकाई
(C) 2/3 πr3 घन इकाई
(D) 3/4 πr3 घन इकाई
33. यदि किसी शंकु के वक्र पृष्ठ का क्षेत्रफल 880 cm2 है और त्रिज्या 14 सेमी है, तो इसकी तिर्यक ऊँचाई है
(A) 10cm
(B) 20cm
(C) 40cm
(D) 30cm
34. एक शंकु का आयतन 1570 cm3 है। यदि इसके आधार का क्षेत्रफल 314 cm2 है, तो इसकी ऊँचाई होगी
(A) 10cm
(B) 15cm
(C) 18cm
(D) 20cm
35. यदि एक अर्द्धवृत्त का परिमाप 72 cm है तो इसकी त्रिज्या है (π = 22/7}
(A) 14cm
(B) 21cm
(C) 35cm
(D) 42 cm
36. x- अक्ष पर वह बिन्दु जो बिन्दुओं A(−1, 0) और B(5,0) से समान दूरी पर है, वह है
(A) (0, 2)
(B) (2,0)
(C) (3, 0)
(D) (0, 3)
37. यदि ΔABC के शीर्षों के निर्देशांक A ( X1 y1 ), B( x2, Y2 ) एवं C ( x3, Y3 ) है तो इसके केन्द्रक का निर्देशांक होगा
(A) (x1+ x2+ x3) (y2 + y2 + y3)
(B) x1 – x2 – x3 , y1 – y2 – y3
(C) {x1 + x2 + x3 / 3, y1 + y2+ y3 / 3 }
(D) {x1+ x2 + x3 / 2, y1 + y2 + y3 / 2}
38. cos4 θ – sin4θ बराबर है
(A) 2cos2θ- 1
(B) 2sin2θ – 1
(C) 2sin2θ + 1
(D) 2cos2θ+ 1
39. 4sec2 A – 4tan2 A का मान क्या होगा ?
(A) 0
(B) 4
(C) -4
(D) इनमें से कोई नहीं
40. निम्नलिखित में कौन-सा सत्य है ?
(A) sin 30° = tan 30°
(B) sec45° = cosec 45°
(C) tan 60° = cot 60°
(D) cos45° = sec45°
41. वह रेखा जो किसी वृत्त से एक और केवल एक बिन्दु पर मिलती है, कहलाती है
(A) त्रिज्या
(B) छेदक रेखा
(C) स्पर्श रेखा
(D) व्यास
42. दो समरूप त्रिभुजों के परिमापों का अनुपात 9 : 4 है तो संगत उँचाइयों का अनुपात होगा
(A) 3:2
(B) 9:4
(C) 81:16
(D) 4:9
43. ΔPQR में ST || QR है, PS = x, SQ = x – 2, PT = x + 2 एवं TR = x – 1 है। x का मान होगा
(A) 4 cm
(B) 4.5cm
(C) 3cm
(D) 3.5cm
44. समान्तर श्रेणी 2,6,10,के प्रथम 11 पदों का योगफल है
(A) 240
(B) 242
(C) 248
(D) 200
45. समान्तर श्रेणी √7, √28, √63, का चौथा पद क्या है?
(A) √70
(B) √84
(C) √98
(D) √112
46. k के किस मान के लिए द्विघात समीकरण 9x2 + 3kx + 4 = 0 के मूल समान हैं?
(A) ± 5
(B) ± 4
(C) + 3
(D) ± 9
47. द्विघात समीकरण x2 + x + 5 = 0 के मूलों की प्रकृति है
(A) वास्तविक और समान
(B) वास्तविक और असमान
(C) अवास्तविक
(D) इनमें से कोई नहीं
48. 156 के अभाज्य गुणनखंडों में 2 का घातांक क्या है ?
(A) 2
(B) 1
(C) 3
(D) 4
49. द्विघात बहुपद में शून्यकों की अधिकतम संख्या होती है
(A) 1
(B) 2
(C) 3
(D) 4
50. यदि p(x) = q(x) g(x) और p(x) का घात = 7 एवं g(x) का घात = 3 तो p(x)/ g(x) का घात होगा
(A) 3
(B) 4
(C) 5
(D) 7
51. यदि बहुपद p(x) का एक शून्यक -2 है तो निम्नलिखित में कौन p (x) का एक गुणनखंड होगा ?
(A) x – 2
(B) x + 2
(C) x – 1
(D) x + 1
52. प्रत्येक सांत दशमलव भिन्न किस प्रकार की परिमेय संख्या का दशमलव रूप है ?
(A) अपरिमेय
(B) परिमेय
(C) पूर्णांक
(D) इनमें से कोई नहीं
53. 5005 के कितने गुणनखंड हैं ?
(A) 2
(B) 4
(C) 6
(D) 7
54. x(5 + 4x) में बहुपद का घात है
(A) 0
(B) 1
(C) 2
(D) 3
55. दो रैखिक समीकरणों के आलेख सामान्तर रेखाएँ हैं, तब रैखिक समीकरण युग्म का
(A) कोई हल नहीं है
(B) एक हल है
(C) दो हल है
(D) अनगिनत हल है
56. sin 45° का मान होगा
(A) 1/2
(B) 1/√2
(C) 1
(D) √3/2
57. यदि cos(α +β) =0 sin(α – β) = ?
(A) sinα
(B) cosβ
(C) sin2α
(D) cos2β
58. sin2 θ + 1/1 + tan2θ का मान क्या होगा ?
(A) 1
(B) 0
(C) sin0
(D) 1/2
59. यदि बहुपद x2 – kx + 8 के शून्यकों का योग 6 है, तो k का मान होगा
(A) 8
(B) – 8
(C) – 6
(D) 6
60. किसी त्रिभुज का केन्द्रक (3,0) है और उसके दो शीर्ष (2, 3) एवं ( 1, -4) है तो तीसरा शीर्ष है
(A) (5, 2)
(B) (1, 3)
(C) (6, 1)
(D) (2, – 3)
प्रश्न- 0.254 को परिमेय संख्या के रूप में लिखें।
उत्तर– माना कि x = 0.254
⇒ x = 0.2545454…
दोनों ओर 10 से गुणा करने पर,
10x = 2.545454 … (i)
फिर समीकरण (i) के दोनों ओर 100 से गुणा करने पर,
1000x = 254.545454 … (ii)
अब समीकरण (i) को समीकरण (ii) में से घटाने पर,
1000x – 10x = 254 – 2
⇒ 990x = 252
∴ x = 252 / 990 = 14/55
अर्थात् 0.254 = 14/55 ; Ans
प्रश्न- सिद्ध करें कि √2 एक अपरिमेय संख्या है।
उत्तर– यदि संभव हो तो माना कि √2 एक परिमेय संख्या है।
∴ √2 = p/q (p एवं q पूर्णांक है तथा p एवं q में 1 के अतिरिक्त कोई q उभयनिष्ठ गुणनखंड नहीं है एवं q ≠ 0 है।
अब दोनों ओर वर्ग करने पर,
2 = p2 / q2 = 2q = p2 / q
यहाँ 2q एक पूर्णांक है एवं p2 / q एक भिन्न है।
∴ पूर्णांक ≠ भिन्न
अतः √2 को एक परिमेय संख्या मानना गलत है।
∴ √2 एक अपरिमेय संख्या है।
प्रश्न- p के किस मान के लिए रैखिक समीकरण युग्म का अद्वितीय हल है ? 2x + 2 y + 2 = 0, 4x + py + 8 = 0
उत्तर– 2x + 2 y + 2 = 0; 4x + py + 8 = 0
यहाँ पर, a1 / a2 = 2 / 4 , b1 / b2 = 2 / p एवं c1 / c2 = 2 / 8
चूँकि दिये गये समीकरण का हल अद्वितीय है।
∴ a1 / a2 ≠ b1 / b2 = 2 / 4 ≠ 2 / p = 2p ≠ 8
∴ P ≠ 8 / q = p ≠ 4
अतः 4 के अतिरिक्त p के किसी भी मान के लिए दिये गए समीकरणों के निकाय का अद्वितीय हल होगा।
प्रश्न- एक आयताकार बाग जिसकी लम्बाई, चौड़ाई से 4 मी अधिक है, का अर्द्ध परिमाप 36 मीटर है। बाग की विमाएँ ज्ञात करें ।
उत्तर– माना कि आयताकार बाग की लम्बाई = x मी
चौड़ाई = y मी
∴ प्रश्नानुसार, x = y + 4
आयताकार बाग का परिमाप = 2 (लं० + चौ०) = 2 (x + y)
∴ अर्द्धपरिमाप = x + y
अर्थात् x + y = 36
⇒ y + 4 + y = 36 [x = y + 4]
⇒ 2y = 32 :: y = 16 मी
अतः x= y + 4 = 16 + 4 = 20 मी
∴ लम्बाई = 20 मी, चौड़ाई = 16 मी० ; Ans.
प्रश्न- यदि बहुपद f (x) = 2x2 – 7x + 3 का शून्यक p तथा q है। P2 + q2 का मान ज्ञात करें ।
उत्तर– f(x) = 2x2 – 7x + 3
यहाँ पर, a = 2, b= -7 एवं c = 3
∴ f (x) के दो शून्यक p एवं q हैं।
∴ p + q = -b / a = -(-7) / 2 / 2 = 7/2
p · q = c/a = 3/2
∴ p2 + q2 = (p + q)2 – 2pq
= {7/2} – 2 x 3/2 = 49/4 -3 = 49 – 12 / 4 = 37 / 4
∴ p2 + q2 = 37/4; Ans
प्रश्न- यदि बहुपद x3 – mx2 – 2nax + na2 का एक गुणनखंड (x – a ) हो, .तो सिद्ध करें कि a = m + n तथा a ≠ 0.
उत्तर– मान लिया कि p(x) = x3– mx2 – 2nax + na2
∴ p(x) का एक गुणनखंड (x – a) है।
∴ p(a) = 0
⇒ a3 – ma2 – 2na · a + na2 = 0
⇒ a3– ma2 – 2na2 + na2 = 0
⇒ a3 – ma2 – na2 = 0
⇒ a2 (a – m – n) = 0
⇒ a – m – n; proved
प्रश्न- दो क्रमागत धनात्मक पूर्णांक ज्ञात करें जिनके वर्गों का योग 365 है।
उत्तर– मान लिया कि दो क्रमागत धन पूर्णांक x एवं x + 1 है।
प्रश्नानुसार, x2+ (x + 1)2 = 365
⇒ x2 + x2 + 2x + 1 -365 = 0
⇒ 2x2 + 2x – 364 = 0
⇒ x2 + x – 182 = 0
⇒ x2 + 14x – 13x – 182 = 0
⇒x(x + 14) – 13 (x + 14) = 0
⇒ (x – 13) (x + 14) = 0
∴ x = 13 या, x = -14
∴ पहला धन पूर्णांक = x = 13
दूसरा धन पूर्णांक = x +1=13 + 1 =14; Ans.
प्रश्न- यदि x = -2 द्विघात समीकरण 4x2 – 3mx + 5 = 0 का एक मूल हो, तो m का मान ज्ञात करें।
उत्तर– दिया गया द्विघात समीकरण है— 4x2 – 3mx + 5 = 0
अब x = – 2 रखने पर,
4(-2)2 – 3m(-2) + 5 = 0
⇒ 16 + 6m + 5 = 0
⇒ 6m + 21 = 0
∴ 6m= -21
यां, m = -21 / 6 = -7/2 ∴ m= -7/3; Ans
प्रश्न- किसी सामांतर श्रेणी में 50 पद हैं, जिनका तीसरा पद 12 और अंतिम 106 है। इसका 29वाँ पद ज्ञात करें ।
उत्तर– n 50, t3 = 12, I = 106, T29 = ?
माना कि दी गई समांतर श्रेणी का प्रथम पद ‘a’ तथा सार्व अन्तर ‘d’ है।
∴ T3 = 12
Tn = a + (n – 1)d = T3 = a + (3 -1)d
⇒ 12 = a + 2d = a + 2d = 12 (…i)
फिर T50 = 106 ⇒ a + 49d = 106 (…ii)
समीकरण (ii) में से समीकरण (i) को घटाने पर, हम पाते हैं कि
47d = 94 ∴ d = 94/47 = 2
समीकरण (i) में ‘d’ का मान रखने पर,
a + 2d = 12 ⇒ a + 2 x 2 = 12
∴ a = 12 – 4 = 8
∴ Tn = a + (n – 1)d
∴ T29 = 8 + (29 – 1)2
= 8 + 28 x 2 = 8 + 56 = 64
∴ T29 = 64; Ans
प्रश्न- 8 के प्रथम 15 गुणजों का योग ज्ञात करें।
उत्तर– 8 के गुणज है— 8, 16, 24, 32, 15 गुणज
यहाँ पर, a = 8, d = 16 – 8 = 8, n = 15
अतः 8 के प्रथम 15 गुणजों का योगफल
= Sn = n/2 [2a + (n – 1) d]
∴ S15 = 15/2 [2 x 8 + (15 – 1) 8]
= 15 / 2 [16 + 14 x 8]
= 15 / 2 [ 16 + 112) = 15/2 x 128
= 15 x 64 = 960
∴ S15 = 960 Ans.
प्रश्न- ABCD एक समलम्ब चतुर्भुज है जिसमें AB || DC है और इसके विकर्ण एक दूसरे को बिन्दु ‘O’ पर प्रतिच्छेद करते हैं। दिखाएँ कि AO/BO = CO/DO
उत्तर– ABCD एक समलम्ब चतुर्भुज है, जिसमें AB || CD है।

सिद्ध करना है—
AO / BO = CO / DO
प्रमाण—
ΔAOB एवं ΔCOD में,
∠OAB = ∠OCD
∠AOB = ∠ODC
∴ ΔAOB ~ ΔCOD
अतः दोनों त्रिभुजों की संगत भुजाएँ समानुपाती होंगी
∴ BO/DO = AO/CO ⇒ CO/DO = AO/BO ⇒ AO/BO = CO/DO; Proved
प्रश्न- एक समकोण त्रिभुज की ऊँचाई इसके आधार से 7cm कम है। यदि कर्ण 13cm का हो तो अन्य दो भुजाएँ ज्ञात करें।
उत्तर– ABC एक समकोण त्रिभुज है, जिसमें
∠AOB = 90°
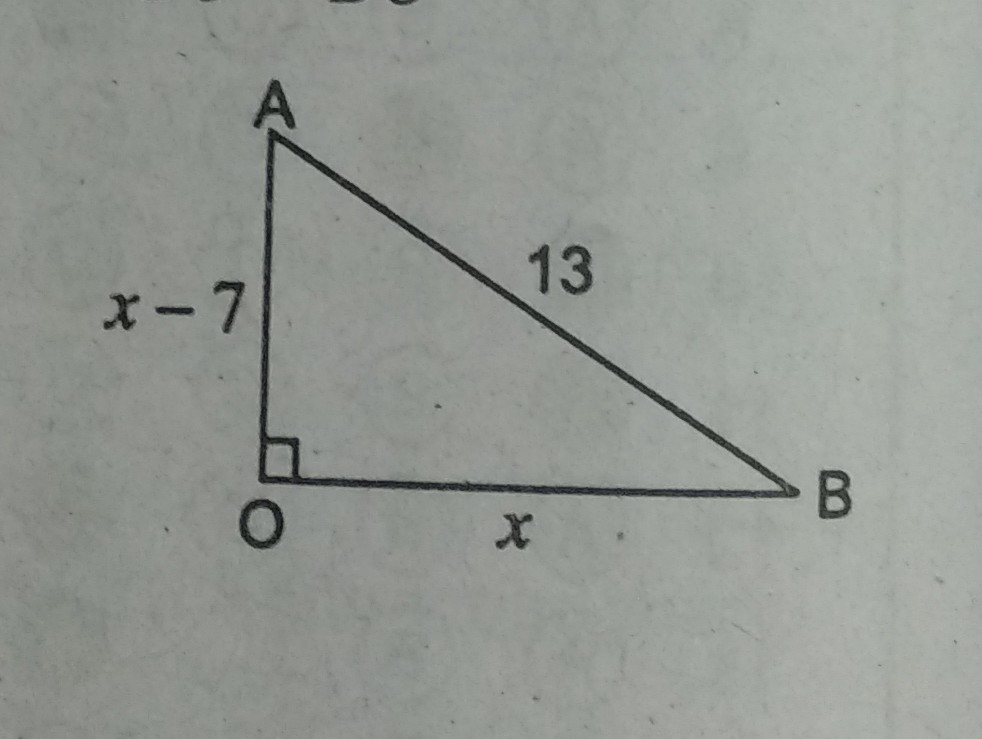
दिया गया है कि कर्ण (AB) = 13cm
प्रश्नानुसार, माना कि OB = x
∴ AO = x – 7
ΔAOB में, OA2 + OB2 = AB2
⇒ (x – 7)2 + x2 = 132
⇒ x2 – 14x + 49 + x2 = 169
⇒ 2x2 – 14x + 49 – 169 = 0
⇒ x2 – 7x – 60= 0
⇒ x2 – 12x + 5x – 60 = 0
⇒ x(x – 12) + 5 (x – 12) = 0
⇒ (x – 12) (x + 5) = 0
∴ x = 12 या x = – 5 (संभव नहीं है।)
अतः, OB = x = 12cm
OA = x – 7 = 12 – 7 = 5cm; Ans.
प्रश्न- सिद्ध करें कि किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ सामांतर होती हैं।
उत्तर– मान लिया कि AOB दिये गए वृत्त का व्यास है तथा A एवं B बिन्दु पर स्पर्श रेखाएँ l एवं m खींची गई है।
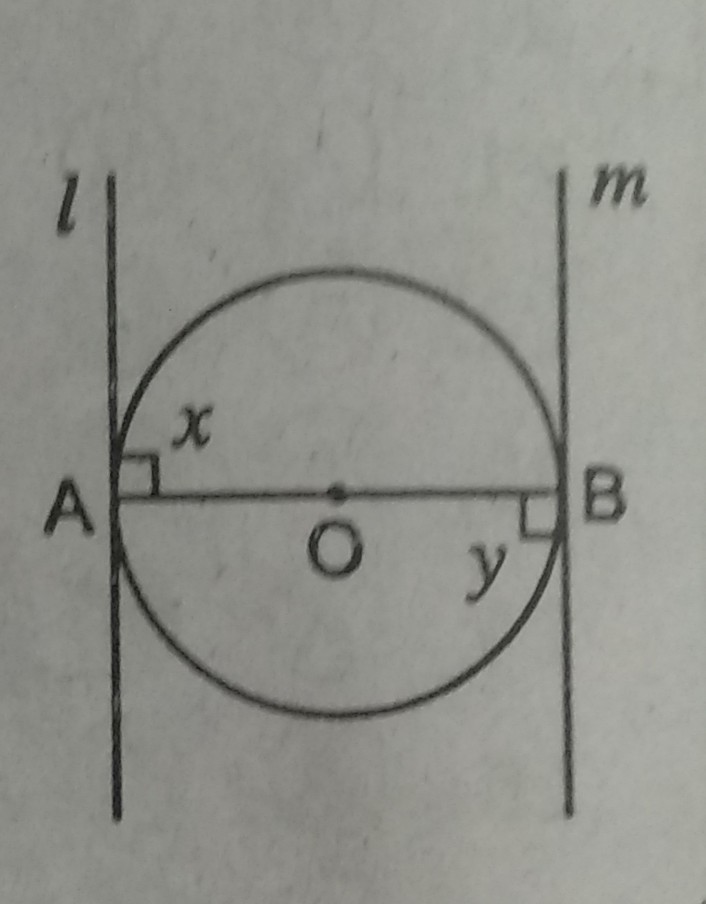
सिद्ध करना है— l ll m
प्रमाण— चूँकि OA वृत्त की त्रिज्या है एवं l एक स्पर्श रेखा है।
∴ ∠x = 90°
इसी प्रकार OB वृत्त की त्रिज्या है एवं m एक स्पर्श रेखा है।
∴ ∠y = 90°
अतः ∠x = ∠y, जो कि एकान्तर कोणों का एक युग्म है।
∴ l ll m होगा।
प्रश्न- सिद्ध करें कि sinθ / 1 + cosθ + 1 + cosθ / sinθ = 2cosecθ
उत्तर– L.H.S = sinθ / 1 + cosθ + 1 + cosθ / sinθ
= sin2 θ + (1 + cosθ)2 / (1 + cosθ) sinθ = sin2θ + 1 + 2 cosθ + cosθ + cos2 θ / (1 + cosθ) sinθ
= sin2 θ + cos2 θ + 1 + 2 cosθ / (1 + cosθ) sinθ
= 1 + 1 + 2cosθ / (1 + cos θ) sinθ= 2 + 2 cosθ / (1 + cosθ) sinθ
= 2(1 + cosθ) / (1 + cosθ) sinθ = 2x 1/ sinθ
= 2 cosecθ = R.H.S ; Proved
प्रश्न- मान ज्ञात करें— 5 cos2 60° + 4sec2 30° – tan2 45° / sin2 30° + cos2 30°
उत्तर– 5cos2 60° + 4sec230° – tan245° / sin2 30° + cos2 30°
= 5{1/2}2 + 4{2/√3}2 – (1)2/ {1/2}2 + {√3/2}2 = 5/4 + 16/3 – 1 / 1/4 + 3/4 = 15 + 64 – 12 /12 / 1+ 3 / 4
= 79 – 12 / 12 / 4 /4 = 67/12 x 4/4 = 67/12 = 5 , 7/12; Ans
प्रश्न- एक समचतुर्भुज का क्षेत्रफल ज्ञात करें जिसके शीर्ष क्रमानुसार (3, 0), (4, 5), ( – 1, 4) और (- 2, – 1) है।
उत्तर– दूरी सूत्र से,
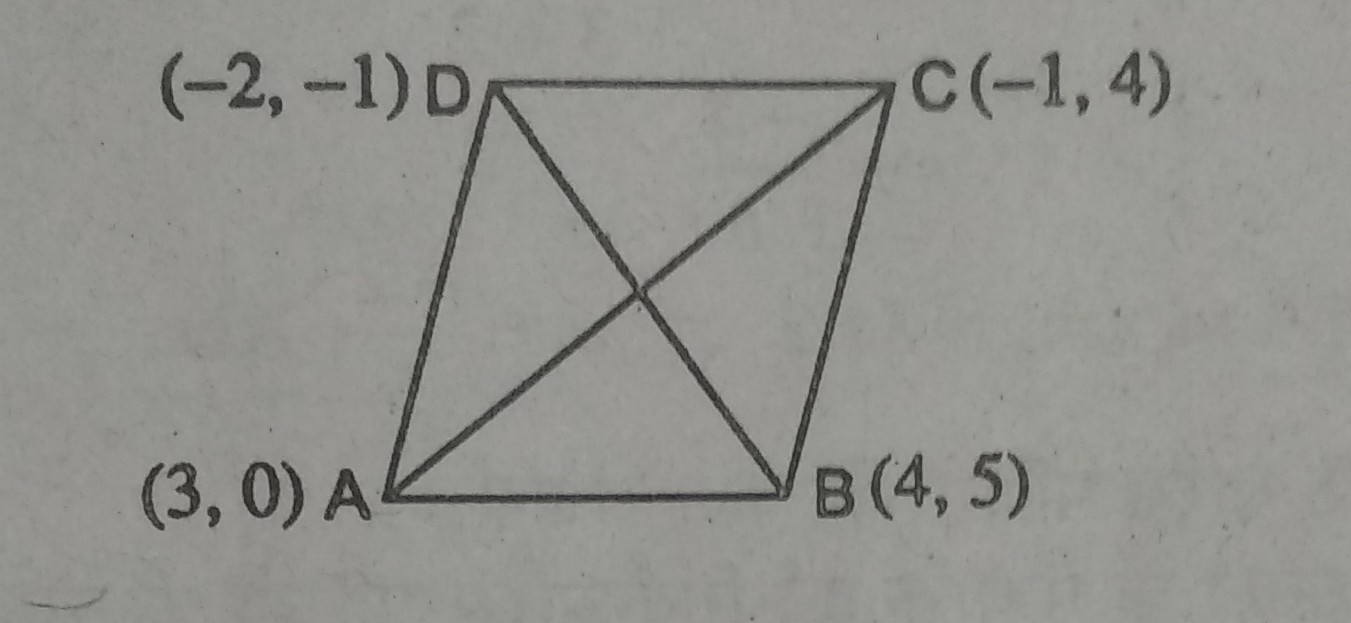
विकर्ण AC = √[3 – (-1)]2 + (0 – 4)2
= √(3 + 1)2 + (-4)2 = √16 + 16 = √32 = 4√2
विकर्ण BD = √[4–(−2)]2 + [5 –(−1)]2
= √(4 + 2)2 + (5 + 1)2 = √36 + 36 = √72 = 6√2
∴ समचतुर्भुज ABCD का क्षेत्रफल
= 1/2 x AC x BD = 1/2 x 4√2 x 6√2
= 1/2 x 4 x 6 x 2 = 24 वर्ग इकाई ।
प्रश्न- बिन्दुओं (4, – 1) और (-2,-3) को जोड़ने वाले रेखाखंड को सम-त्रिभाग करने वाले बिन्दुओं का निर्देशांक ज्ञात करें ।
उत्तर–
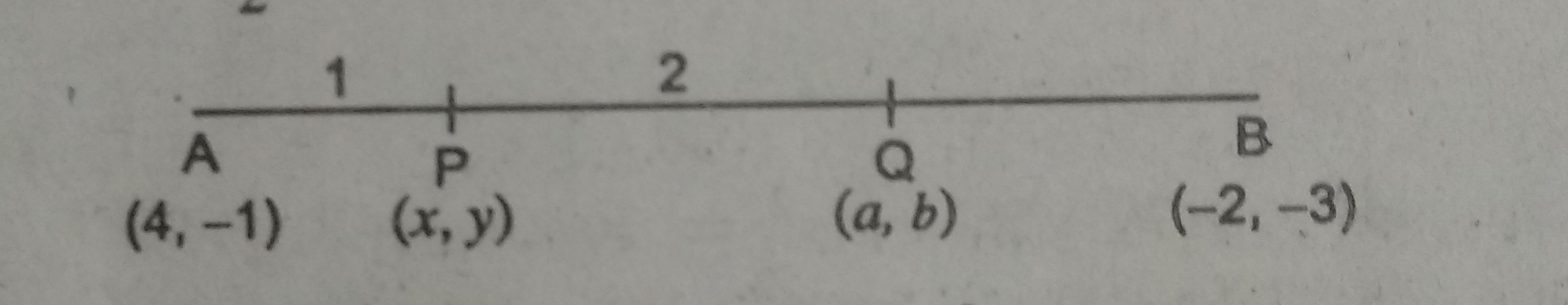
यहाँ पर x1 = 4, y= -1 , x2 = -2, y2= -3
माना कि बिन्दु P एवं Q, AB को समत्रिभाग करते हैं।
∴ AP = PQ = QB
या AP : PB = 1 : 2 या m1 : m2 = 1 : 2
अत: P का x निर्देशांक = m1 x2 + m2 x1 / m1 + m2
= 1x(-2) + 2 x 4 / 1 + 2 = -2 + 8 /3 = 6/3 = 2
P काy निर्देशांक = m1y2+ m2y1 / m1 + m2
= 1(-3) + 2(-1) / 1 + 2 = -3 – 2 / 3 = -5)3
अतः P का निर्देशांक = {2, – 5/3}; Ans
अब बिन्दु Q, PB का मध्य बिन्दु है।
अतः Q का निर्देशांक = x1+ x2 / 2 , y1 + y2 /2
= 2 + (-2) / 2 , -5/3 + (-3) / 2
= 2 – 2 / 2, -5/3 + (-3) = 2 – 2 /2 , -5/3-3/2
= 0, -5 – 9 / 6 = 0, -14/6 = 0, -7/3
अतः Q का निर्देशांक = {0, -7/4} Ans.
प्रश्न- एक घड़ी की मिनट की सुई जिसकी लम्बाई 14 cm है। इस सुई द्वारा 5 मिनट में रचित क्षेत्रफल ज्ञात करें ।
उत्तर– r = 14 cm
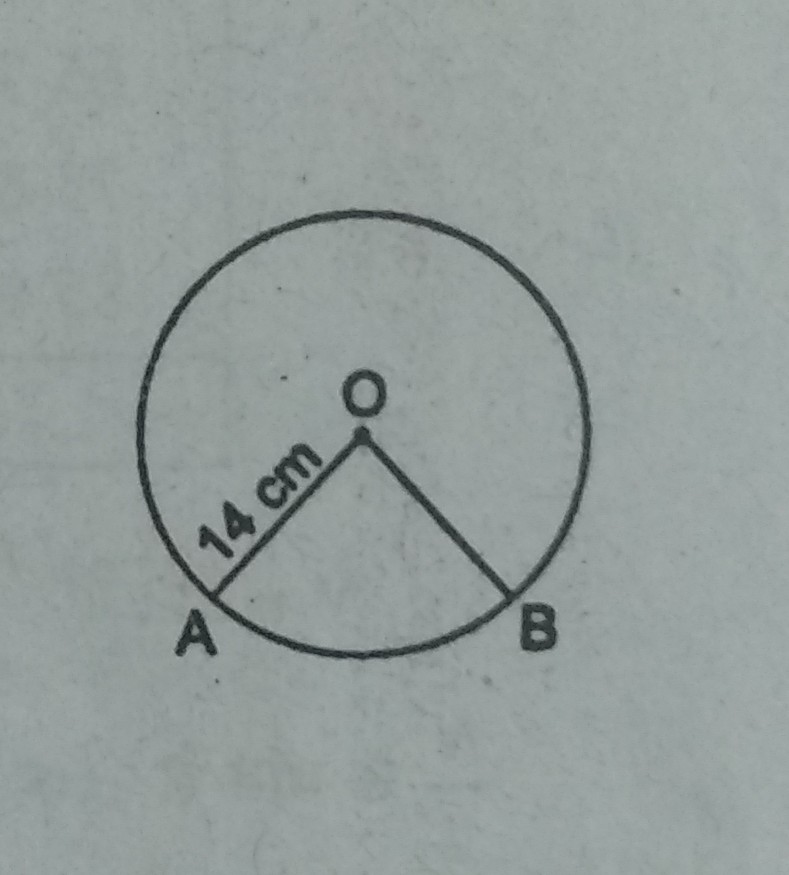
∴ 60 मिनट में मिनट की सुई केन्द्र पर 360° कोण बनाती है।
∴ 5 मिनट में केन्द्र पर बनाया गया कोण
= 360° / 60 x 5 = 30°
अतः 5 मिनट में रचित क्षेत्रफल = πr2θ / 360°
= 22 x 14 x 14 x 30° / 7 x 360° = 154 / 3 cm2; Ans
प्रश्न- किसी कार के पहिए का व्यास 80cm है। यदि कार 66 km प्रति घंटे की चाल से चल रही है तो 10 मिनट में प्रत्येक पहिया कितने चक्कर लगाता है ?
उत्तर– पहिया की चाल = 66 km/h = 66 x 1000 x 100 / 60 cm/min
= 11 x 100 x 100 cm/min
∴ पहिया द्वारा 10 मिनट में तय की गई दूरी = 11 x 100 x 100 x 10
अब पहिया का वयास = 80cm
∴ त्रिज्या = 40cm
पहिया द्वारा 1 चक्कर में तय की गई
= 2πr = 2 x 22/7 x 40
अतः चक्करों की संख्या
= 11 x 100 x 100 x 10 x 7 / 2 x 22 x 40 = 4375; Ans
प्रश्न- उस गोले का पृष्ट क्षेत्रफल निकालें जिसका व्यास 14 सेमी है।
उत्तर– गोले का वयास = 14cm
∴ त्रिज्या = 7 cm
अतः गोले का पृष्ठीय क्षेत्रफल = 4nr2
= 4 x 22/7 x 7 x 7
= 88 x 7 = 616cm2; Ans.
प्रश्न- दो बेलनों के आयतन समान हैं तथा उनकी ऊँचाइयाँ 1 : 2 के अनुपात में हैं। उनकी त्रिज्याओं का अनुपात क्या होगा ?
उत्तर– मान लिया कि पहले बेलन की ऊँचाई h1 एवं दूसरे बेलन की ऊँचाई h2है। इसी प्रकार पहले बेलन की त्रिज्या r2 एवं दूसरे बेलन कि त्रिज्या r2 है।
प्रश्नानुसार, h1 : h2= 1 : 2
= h1 / h2 = 1/2
दिया गया है कि दोनों बेलनों के आयतन समान हैं।
∴ πr1 h1= πr2 h2
⇒ r1 h1= r22 h2
⇒ r12 / r22 = h2 / h2
⇒ r12 / r22 = 2/1 = {√2 / 1}2
⇒ r1 / r2 = √2 / 1
∴ r1 : r2 = √2 : 1; Ans.
प्रश्न- नीचे दी गई बारंबारता सारिणी में प्रदत्त आँकड़े की माध्यिका ज्ञात करें।
| वर्ग अंतराल | 45 – 55 | 45 – 55 | 65 – 75 | 75 – 85 |
85 – 95
|
| बारंबारता | 3 | 10 | 11 | 8 | 3 |
उत्तर–
| C.I | f | c.f. |
| 45 – 55 | 3 | 3 |
| 55 – 65 | 10 | 13 |
| 65 – 75 | 11 | 24 |
| 75 – 85 | 8 | 32 |
| 85 – 95 | 3 | 35 |
| N= 35 |
∴ N = 35 ∴ N/2 = 35/2 = 17.5
N/2 के मान से ठीक अधिक संचयी बारंबारता 24 है तथा इसका संगत वर्ग अन्तराल (65-75) है।
∴ माध्यिका वर्ग = 65-75
अतः I = 65, N/2 = 17.5 c.f. = 13, f = 1, h = 10
N/ 2 – c.f.
माध्यिका = l + f x h = 65 + 17.5 – 3 / 11 x 10
= 65 + 4.5 x 10 / 11 = 65 + 45/11 = 65 + 4.09 = 69.09
माध्यिका = 60.09; Ans
प्रश्न- माध्यिका किसे कहते हैं ? इसका सूत्र लिखें।
उत्तर– माध्यिका— यदि दिये गए आँकड़ों के सभी प्रेक्षणों को आरोही या अवरोही क्रम में व्यवस्थित किया जाय तो इन प्रेक्षणों के समुच्चय के बीचों बीच मान को अर्थात् इनके केन्द्रीय मान को माध्यिका कहा जाता है।
N/2 – c. f.
माध्यिका = l + f x h
प्रश्न- दो पासे एक साथ फेंके जाते हैं। दोनों पासों पर प्राप्त अंकों का योग 10 या 10 से कम होने की प्रायिकता ज्ञात करें।
उत्तर– दो पासों को एक साथ फेंकने पर सभी संभावित परिणाम निम्नवत् हैं—
(1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6)
(2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6)
(3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6)
(4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6)
(5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6)
(6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6)
10 या 10 से कम आने की प्रायिकता
= 10 या 10 से कम आने की संख्या / अभिप्रयोगों की कुल संख्या = 33/36 = 11/12; Ans.
प्रश्न- अच्छी प्रकार से फेटी गई 52 पतों की ताश की गड्डी में से एक पत्ता निकाला जाता है। इसकी प्रायिकता ज्ञात करें कि वह पत्ता एक इक्का है।
उत्तर– चूँकि पत्ते अच्छी तरह से फेंट दिए जाते हैं इसलिए परिणाम समसंभावी होंगे। स्पष्टतः सभी संभव परिणामों की कुल संख्या = 52.
एक गड्डी में 4 इक्के होते हैं। माना कि ‘एक इक्का होना’ की घटना को E द्वारा व्यक्त किया जाता है।
∴ अनुकूल परिणामों की संख्या = 4
अतः P(E) = P (एक इक्का) = 4/52 = 1/13
प्रश्न- बिन्दु P(m, 6) दो बिन्दुओं A (- 4, 3) एवं B (2, 8) को मिलाने वाली रेखा को किस अनुपात में बाँटता है। m का मान भी ज्ञात करें ।
उत्तर–
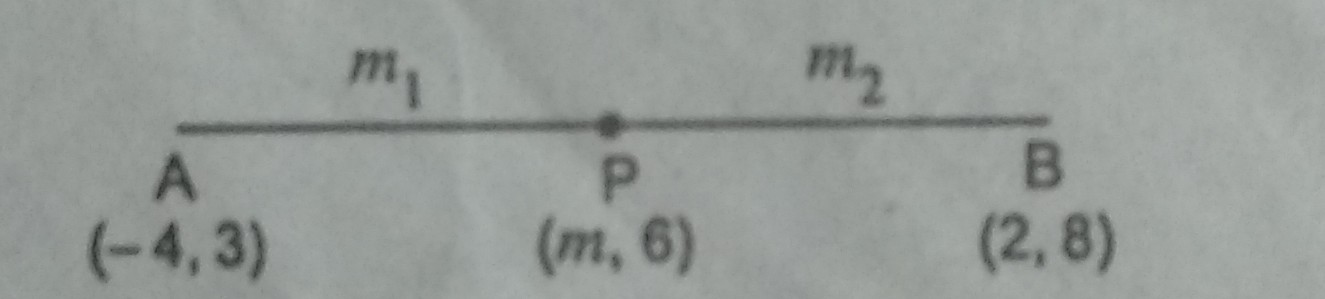
माना p सरल रेखा AB को m1 : m2 में विभाजित करता है।
अत: p का ‘y’ निर्देशांक = M1y2 + m2y1 / m1 + m2
⇒ 6 = m1 x 8 + m2 x 3 / m1 + m2
⇒ 8m1 + 3m2= 6m1 + 6m2
⇒ 8m1 – 6m1 = 6m2 – 3m2
⇒ 2m1 = 3m2 = m1 / m2 = 3/2
∴ m1 : m2 = 3 : 2
अर्थात् बिन्दु P, AB को 3 : 2 में बाँटता है।
अब P का x निर्देशांक = m1 x2+ m2x1 / m1 + m2
⇒ m = 3 x 2 + 2 x (-4) / 3 + 2 = 6 – 8 / 5
∴ m = -2 / 5
इस प्रकार m1 : m2 = 3 : 2 :: m = -2 / 5;Ans
प्रश्न- सारस पक्षियों के समूह का एक-चौथाई भाग कमल के पौधे के इर्द-गिर्द घूम रहे हैं। कुल संख्या के 1/9 भाग के साथ-साथ 1/4 भाग एवं उनकी कुल संख्या के वर्गमूल का 7 गुना एक पहाड़ी पर घूम रहे हैं तथा शेष 56 पक्षी वकुला (Vakula) के पेड़ों पर बैठे हैं। सारस पक्षियों की कुल संख्या ज्ञात करें।
उत्तर– माना कि सारस पक्षियों की कुल संख्या = x
अतः कमल के पौधे के इर्द-गिर्द सारस पक्षियों की संख्या = 1 / 4 x
पहाड़ी पर घूम रहे पक्षियों की संख्या = 1/9 x + 1/4 x + 7√x
बगुला के पेड़ों पर सारस पक्षियों की संख्या = 56
अतः प्रश्नानुसार, 1/4x + 1/9x +1/4x + 7√x + 56 = x
माना कि x = y2 :: √x = y
अतः 1/4y2 + 1/9y2 + 1/4y2 + 7y + 56 = y2
⇒ 7y + 56 = y2– 1/4y2 – 1/9y2 – 1/4y2
⇒ 7y + 56 36y2– 9y2 – 4y2 – 9y2 / 36
⇒ 36(7y + 56) = 14y2 = 36 x 7 (y + 8) = 14y2
⇒ 18(y + 8) = y2 = y2 – 18y – 144 = 0
⇒ y2– 24y + 6y – 144 = 0
⇒ y(y – 24) + 6 (y – 24) = 0
⇒ (y – 24) (y + 6) = 0
∴ y = 24 या y = -6
यदि y = -6 तो y2 = 36
या x = 36, जो कि संभव नहीं है, क्योंकि शेष सारस पक्षियों की संख्या ही 56 है।
दि y = 24 तो y2 = 576 ⇒ y = 576
अतः सारस पक्षियों की संख्या = 576; Ans.
प्रश्न- एक मीनार के पाद से एक भवन शिख़र का उन्नयन कोण 30° है, और भवन के पाद से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार की ऊँचाई 50 मीटर है तो भवन की ऊँचाई ज्ञात करें ।
उत्तर–
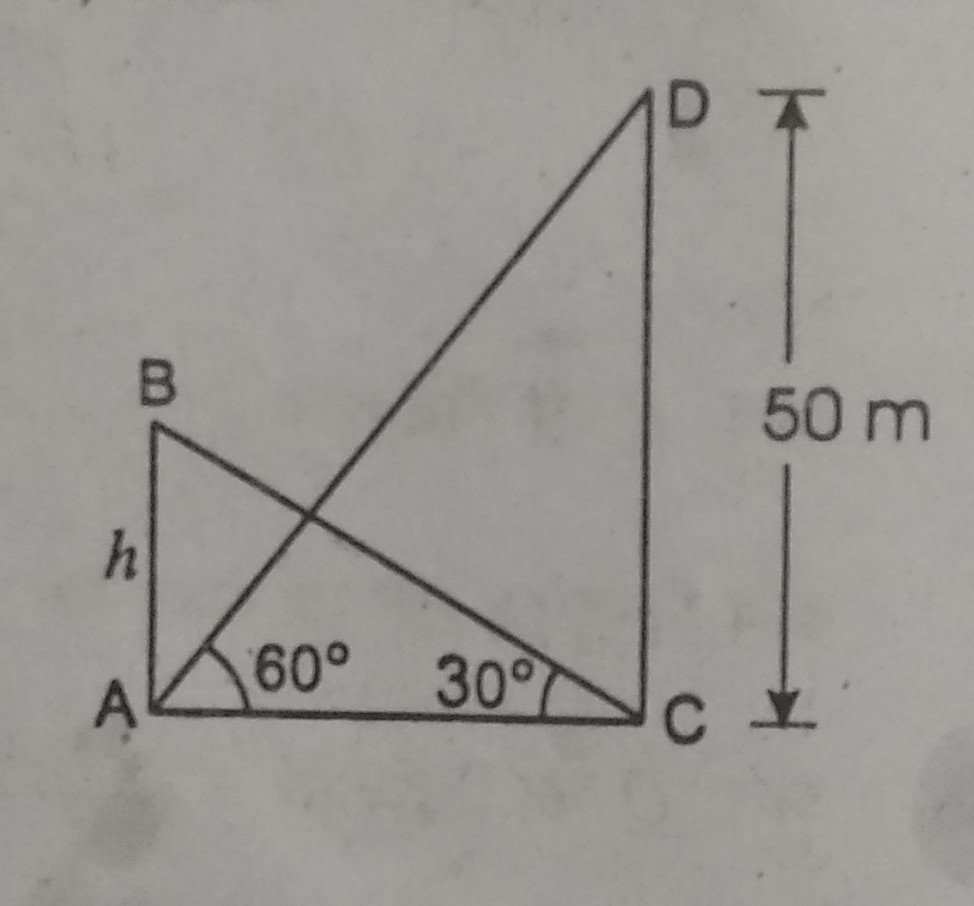
मानलिया कि AB एक भवन है
जिसकी ऊँचाई h है। CD एक मीनार है
जिसकी ऊँचाई 50 मी दी गई है ।
प्रश्नानुसार, ∠CAD = 66
तथा ∠ACB = 30°
समकोण ΔBAC में,
tan36° = AB / AC
⇒ 1 / √3 = h / AC
∴ AC = √3h
फिर समकोण ΔACD में,
tan60° = CD / AC
⇒ √3 = 50 / √3h
⇒ 3h = 50 ∴ h = 50 / 3 = 16.67 मी
अतः भवन की ऊँचाई = 16.67 मी; Ans.
प्रश्न- किसी त्रिभुज में एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर हो तो सिद्ध करें कि पहली भुजा के सामने का कोण समकोण होता है।
उत्तर– दिया गया है – ABC एक त्रिभुज है

जिसमें AC2 = AB2+ BC22
सिद्ध करना है— ∠ABC = 90°
रचना—एक त्रिभुज DEF इस प्रकार खींचा कि
DE = AB, EF = BC तथा ∠DEF = 90° हो ।
प्रमाण— समकोण ΔDEF में, पाइथागोरस प्रमेय के अनुसार,
DF2 = DE2 + EF2
⇒ DF2 = AB2 + BC2 …(i)
[ रचना से AB = DE एवं BC = EF]
लेकिन दिया गया है कि
AC2 = AB2+ BC2 (…ii)
अतः समीकरण (i) एवं (ii) से,
AC2 = DF2 या, AC = DF
अब ΔABC एवं ΔDEF में,
AB = DE (रचना से)
BC = EF (रचना से)
तथा, AC = DF (प्राप्त किया गया)
∴ ΔABC = ΔDEF (SSS सर्वांगसमता से)
अतः ∠ABC = ∠DEF (C.P.C.T. से) Proved.
प्रश्न- एक खिलौना 3.5 cm त्रिज्या वाले एक शंकु के आकार का है जो त्रिज्यावाले एक अर्द्धगोले पर अध्यारोपित है। इस खिलौने की कुल ऊँचाई 15.5 cm है। इस खिलौने का आयतन एवं सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात करें।
उत्तर–
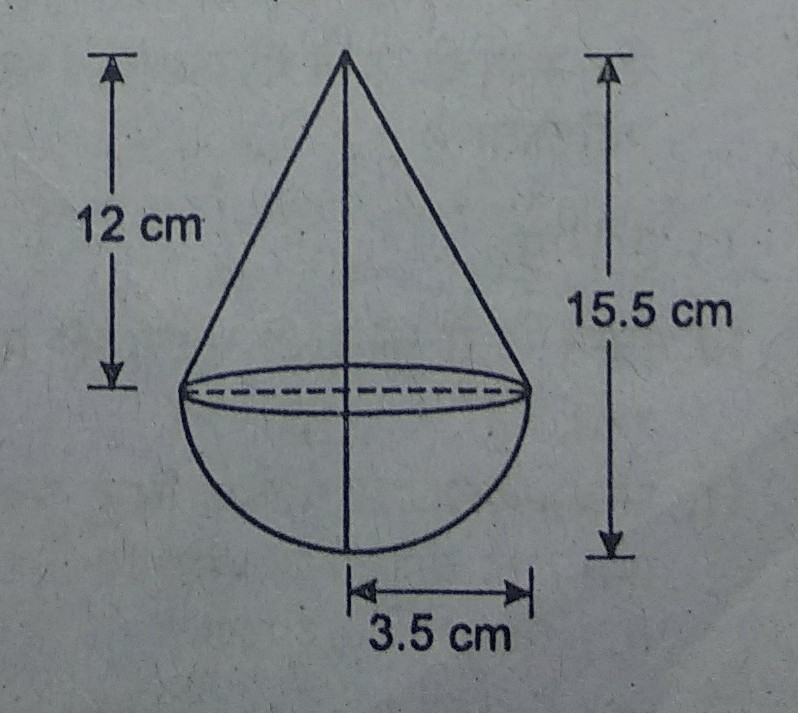
शंकु की त्रिज्या = गोले की त्रिज्या (r) = 3.5cm खिलौने की कुल ऊँचाई
= 15.5cm
∴ शंकु की ऊँचाई (h)
= 15.5 – 3.5 = 12 cm
अब शंकु की तिरछी ऊँचाई (l)
= √h2+ r2
= √(12)2 + (3.5)2
= √144 + 12.25 = √156.25 = 12.5cm
I = 12.25
खिलौने का आयतन = 2/3πr3 + 1/2πr2h
= 1/3πr2 (2r + h)
= 1/3 x 22/7 x 3.5 x 3.5 (2 x 3.5 + 12)
= 1/3 x 11 x 3.5 (7 + 12)
= 1/3 x 11 x 3.5 x 19 = 243.8cm2; Ans
खिलौने के सम्पूर्ण पृष्ठ का क्षेत्रफल
= 2πr2 + πrl = πr (2r + 1)
= 22/7 x 3.5 (2 x 3.5 + 12)
= 11( 7 + 12.5) = 11 x 19.5 = 214.5 cm3 ; Ans
प्रश्न- सिद्ध करें— (i) sinθ – 2 sin3θ / 2 cos3θ – cosθ = tanθ
(ii) √1 + cosθ / 1 – cosθ= cosecθ+ cotθ
उत्तर– (i) L.H.S = sinθ – 2sinθ3θ/ 2cos3θ – cosθ = sinθ (1 – 2sin2θ) / cosθ (2cos2θ – 1)
= sinθ (1 – 2 sin2θ) / cos0 [ 2(1 – sin2θ) – 1]
= sinθ (1 – 2sin2 θ) / cos 0 (2 – m2 θ – 1)
= sinθ(1 – 2sin2 θ) / cosθ (1 – 2 sin2θ) = sinθ / cosθ
= tanθ = R.H.S ; Proved
(ii) L.H.S = √1 + cos θ/ 1 – cosθ
= √(1 + cosθ) (1 + cosθ) / (1 – cosθ) (1 + cosθ)
= √(1 + cosθ)2 / 1 – cos2 θ = √(1 + cosθ)3 / sin2θ
= 1 + cosθ / sinθ = 1 / sinθ + cosθ / sin2θ
= cosecθ+ cotθ = R.H.S ; Proved.
प्रश्न- समीकरण x – y + 1 = 0 और 3x + 2y – 12 = 0 का आलेख खींचें। इन रेखाओं और x- अक्ष से निर्मित त्रिभुज का क्षेत्रफल ज्ञात करें।
उत्तर– दिया गया है कि x – y + 1 = 0
तथा 3x + 2y – 12 = 0
समीकरण (i) से, x − y +1 = 0 ⇒ y = x + 1
मान सारिणी
| x | -1 | 0 | 1 |
| y | 0 | 1 | 2 |
समीकरण (ii) से, 3x + 2y – 12 = 0
⇒ 2y = 12 – 3x ∴ y = 12 – 3x / 2
मान सारिणी
| x | 4 | 2 | 0 |
| y | 0 | 3 | 6 |
चूँकि रेखाएँ AB एवं CD एक दूसरे को बिन्दु P(2, 3) पर प्रतिच्छेद करती है। x- अक्ष एवं AB तथा CD रेखाओं के बीच बना ΔPQR है। जिसका आधार QR = 5 इकाई तथा ऊँचाई PM = 3 इकाई ।
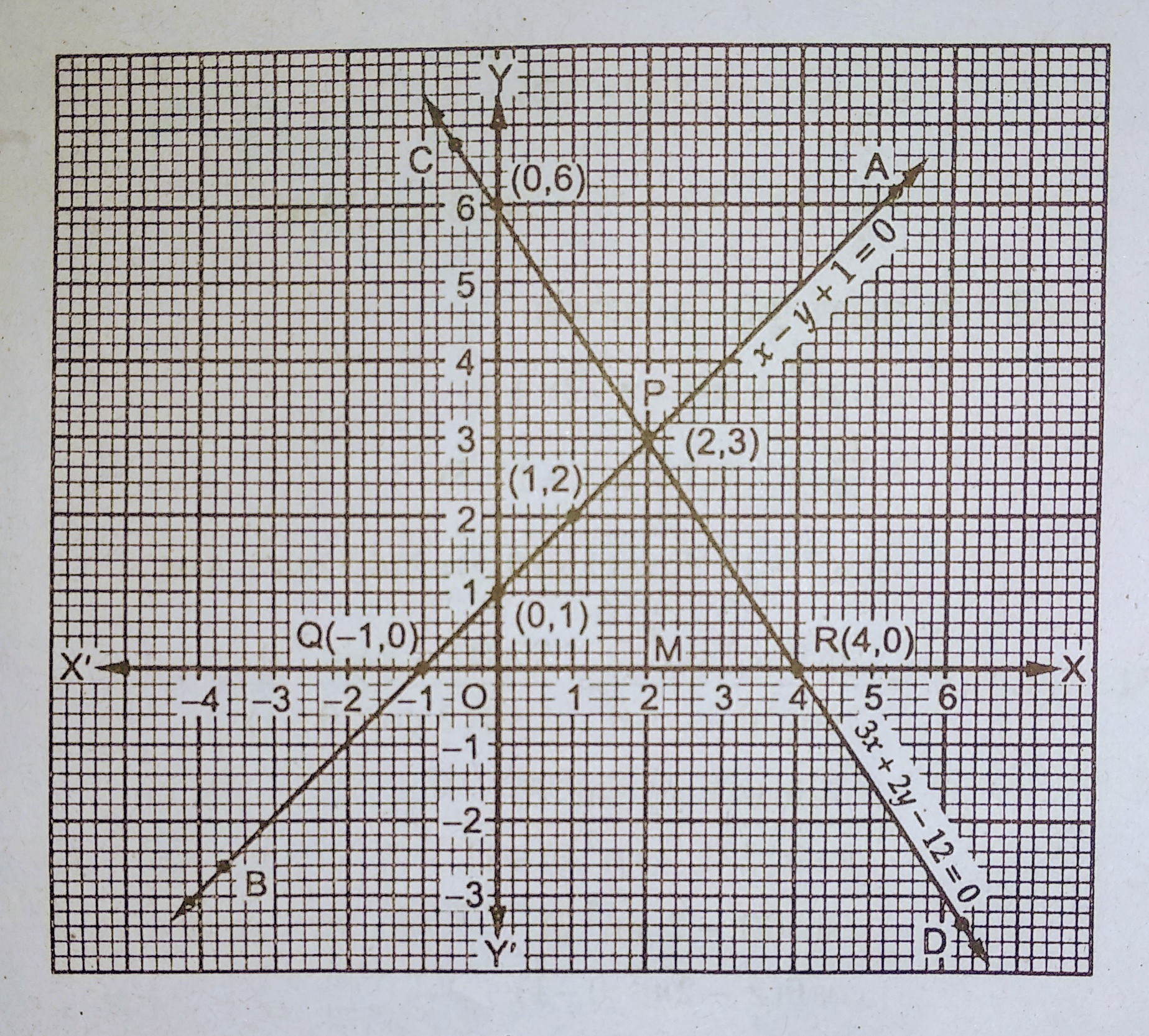
∴ ΔPQR का क्षेत्रफल = 1/2 x QR x PM
= 1/2 x 5 x 3 = 15/2 = 7.5 वर्ग इकाई ।
प्रश्न- त्रिभुज ABC की रचना करें जिसमें BC = 6cm, AB = 5 cm और ∠ABC = 60° हो। फिर एक त्रिभुज की रचना करें जिसकी भुजाएँ ΔABC की संगत भुजाओं की 4/3 गुनी है।
उत्तर– रचना के चरण—
(i) दिये गए मानों से ΔABC की रचना किया जिसमें BC = 6cm, ∠ABC = 60° और AB = 5cm
(ii) BC के नीचे एक न्यूनकोण ∠CBX बनाया।
(iii) BX पर चार बिन्दु B1, B2, B3 इस प्रकार आरोपित और किया कि BB = B1 B2 = B2B3 = B3 B4
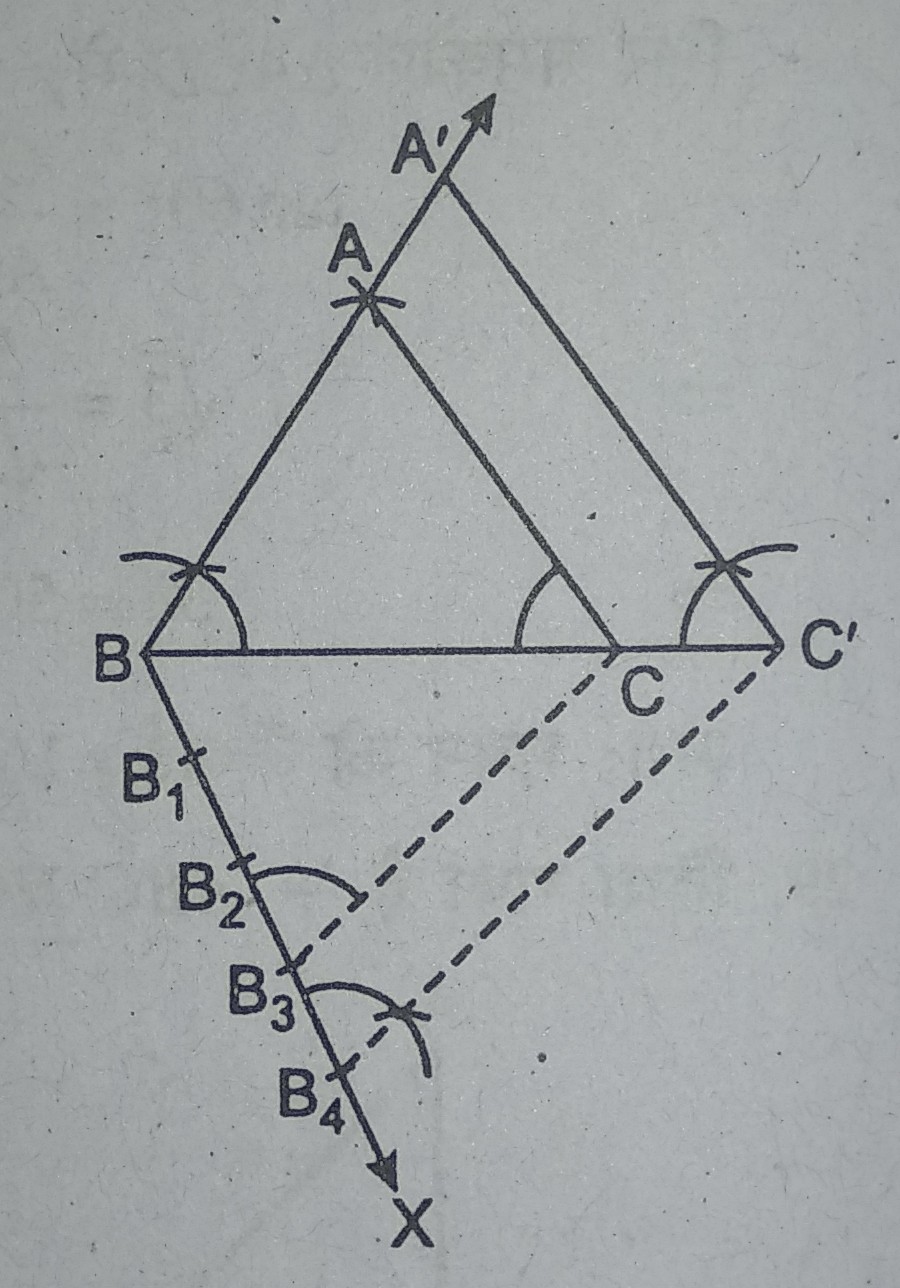
(iv) B3C को मिलाया।
(v) B4 से B3C के सामांतर रेखा खींचा जो BC के बढ़ाये हुए भाग में बिन्दु C’ पर मिलती है।
(vi) फिर C’ से CA के सामांतर एक रेखा खींचा जो BA के बढ़ाये हुए भाग से बिन्दु A’ पर मिलती है ।
(vii) इस प्रकार हमें वांछित ΔA’BC’ प्राप्त हुआ जिसकी भुजाएँ ΔABC की भुजाओं की 4/3 गुनी है।
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here