Bihar Secondary School Sample Paper Solved | BSEB Class 10th Sample Sets with Answers | Bihar Board class 10th Sample Paper Solved | Bihar Board Class 10th mathematics Sample set – 4
Bihar Secondary School Sample Paper Solved | BSEB Class 10th Sample Sets with Answers | Bihar Board class 10th Sample Paper Solved | Bihar Board Class 10th mathematics Sample set – 4
1. एक सिक्का को उछालने पर एक चित्त आने की प्रायिकता है
(A) 1/2
(B) 2/3
(C) 4/3
(D) 5/4
2. ΔABC में AB एवं AC के मध्य बिन्दु क्रमश: D एवं E इस प्रकार हैं कि BC = 8 सेमी, तब DE का मान होगा
(A) 5 सेमी
(B) 3 सेमी
(C) 4 सेमी
(D) 2 सेमी
3. ax2 – bx + c = 0 के मूलों का योगफल होगा
(A) -b/a
(B) b/a
(C) c/a
(D) इनमें से कोई नहीं
4. किसी A.P. के प्रथम पद ‘2’ एवं सार्व अन्तर 3 है, तब A.P. के प्रथम तीन पद होंगे
(A) 2, 6, 9
(B) 2, 5, 8
(C) 2, 6, 10
(D) 2, 5, 9
5. कोण θ वाले त्रिज्यखंड का क्षेत्रफल होगा
(A) θ / 270 x πr3
(B) θ / 360 x πr
(C) θ / 270 x πr2
(D) θ / 360 x πr2
6. निम्न में कौन-सा परिमेय है ?
(A) π
(B) √7
(C) √16/25
(D) 3√3/ √2
7. चरों को आरोही या अवरोही क्रम में रखने पर बीच वाले चर का मान कहलायेगा
(A) माध्य
(B) माध्यिका
(C) बहुलक
(D) इनमें से कोई नहीं
8. किसी वृत्त के व्यास के दोनों किनारों से खींची गई स्पर्श रेखा होती है
(A) समांतर
(B) लम्बवत्
(C) प्रतिच्छेदी
(D) इनमें से कोई नहीं
9. एक साथ दो पासों को उछालने पर प्राप्त संख्याओं का योगफल 7 होने की प्रायिकता है
(A) 1/4
(B) 1/6
(C) 2/3
(D) 3/4
10. निम्न में से कौन-सी घटना की प्रायिकता नहीं हो सकती है ?
(A) 1.1
(B) 0.5
(C) 0.9
(D) 0.1
11. संख्या – रेखा पर प्रत्येक बिन्दु प्रदर्शित करता है ?
(A) एक वास्तविक संख्या
(B) एक प्राकृत संख्या
(C) एक परिमेय संख्या
(D) एक अपरिमेय संख्या
12. एक 6 मीटर ऊँचे वृक्ष की छाया 4 मीटर लम्बी है। उसी समय एक र छाया 50 मीटर है, तो खंभे की ऊँचाई (मीटर में) है
(A) 40
(B) 25
(C) 75
(D) 10
13. तोरण खींचने के लिए वर्ग अन्तरालों को होना चाहिए
(A) समावेशिक
(B) अपवर्जी
(C) दोनों (A) तथा (B)
(D) इनमें से कोई नहीं
14. निम्न में से कौन cot θ के बराबर है ?
(A) sin θ / cos θ
(B) cos θ / sin θ
(C) 1 / sin θ
(D) 1 / cos θ
15. यदि cos A = 1/2 हो, तो 1 – 2 cos2 A का मान है
(A) 1/2
(B) 2/3
(C) 1/4
(D) 1/3
16. निम्नलिखित में किसका दशमलव प्रसार सांत है ?
(A) 3/8
(B) 6/15
(C) 29/343
(D) 17/1536
17. 3. 27 है
(A) एक पूर्णांक
(B) एक परिमेय संख्या
(C) एक प्राकृत संख्या
(D) एक अपरिमेय संख्या
18. प्रथम पाँच विषम संख्याओं का माध्य है
(A) 6
(B) 4
(C) 5
(D) 8
19. बिन्दुओं A(3, 4) और B (– 3, 8) को मिलाने वाले रेखाखंड के मध्य बिन्दु का निर्देशांक है
(A) (0, 12)
(B) (6, 0)
(C) (6, – 4)
(D) (0, 6)
20. बिन्दुएँ (3, 2) और ( -3, 2) दोनों अवस्थित हैं
(A) x-अक्ष पर
(B) y-अक्ष पर
(C) x-अक्ष के एक ही ओर
(D) x-अक्ष के दोनों ओर
21. यदि रैखिक समीकरणों का युग्म संगत है तब उनके द्वारा होती हैं
(A) समान्तर
(B) प्रतिच्छेदी
(C) संपाती
(D) प्रतिच्छेदी या संपाती
22. रैखिक समीकरण युग्म 5x + 2y = 16 एवं 7x – 4y = 2 के हल हैं
(A) x = 2, y = 3
(B) x = 2, y = 1
(C) x = 1, y = 3
(D) x = 0, y = 3
23. रैखिक बहुपद के शून्यकों की संख्या होती है
(A) 2
(B) 1
(C) 3
(D) इनमें से कोई नहीं
24. किसी द्विघात बहुपद के शून्यक यदि 5 एवं – 3 है, तो द्विघात बहुपद होगा
(A) x2 + 2x – 15
(B) x2 – 2x + 15
(C) x2 – 2x – 15
(D) इनमें से कोई नहीं
25. 21 cm त्रिज्या वाले वृत्त के उस चाप की लम्बाई क्या होगी जो वृत्त के केन्द्र पर 60° का कोण अन्तरित करता है ?
(A) 21cm
(B) 22cm
(C) 23cm
(D) 24cm
26. यदि एक वृत्त की परिधि 132 cm है, तो इसकी त्रिज्या है
(A) 66cm
(B) 7 cm
(C) 42cm
(D) 21cm
27. यदि एक शंकु की त्रिज्या 14 cm और इसकी तिर्यक ऊँचाई 15cm हो तो शंकु के वक्र पृष्ठ का क्षेत्रफल होगा
(A) 1276 cm2
(B) 660 cm2
(C) 1376 cm2
(D) 1320 cm2
28. समान ऊँचाई वाले दो बेलनों के आयतनों का अनुपात 9 : 16 है तो उनके वक्रपृष्ठों के क्षेत्रफलों का अनुपात होगा
(A) 9 : 16
(B) 16 : 9
(C) 3 : 4
(D) 4 : 3
29. दी गई आकृति में दो वृत्त एक-दूसरे को बिन्दु 5 पर स्पर्श करते हैं। यदि PR = 4.5cm तो PQ का मान होगा
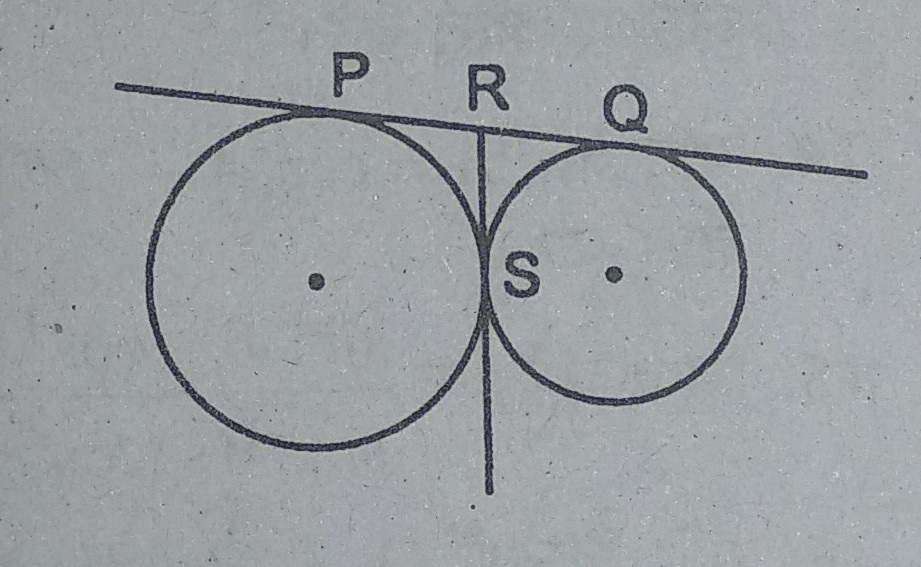
(A) 7cm
(B) 9cm
(C) 13.5cm
(D) 15cm
30. y- अक्ष का समीकरण कहलाता है
(A) y = 0
(B) x = 0
(C) xy = 0
(D) x – y = 0
31. यदि समीकरण bx2 + ax + c = 0 के मूल समान हों तो ‘c’ का मान है
(A) – a2 / 4b
(B) a2 / 4b
(C) a / 2b
(D) -a / 2b
32. यदि बिन्दुएँ (k, 2), (– 3, – 4) तथा (7, – 5) संरेख हों, तो k का मान है
(A) – 60
(B) 60
(C) – 63
(D) 63
33. एक बहुपद f (x) के लिए y = f(x) का ग्राफ नीचे दिखाया गया है। इसके शून्यकों की संख्या है
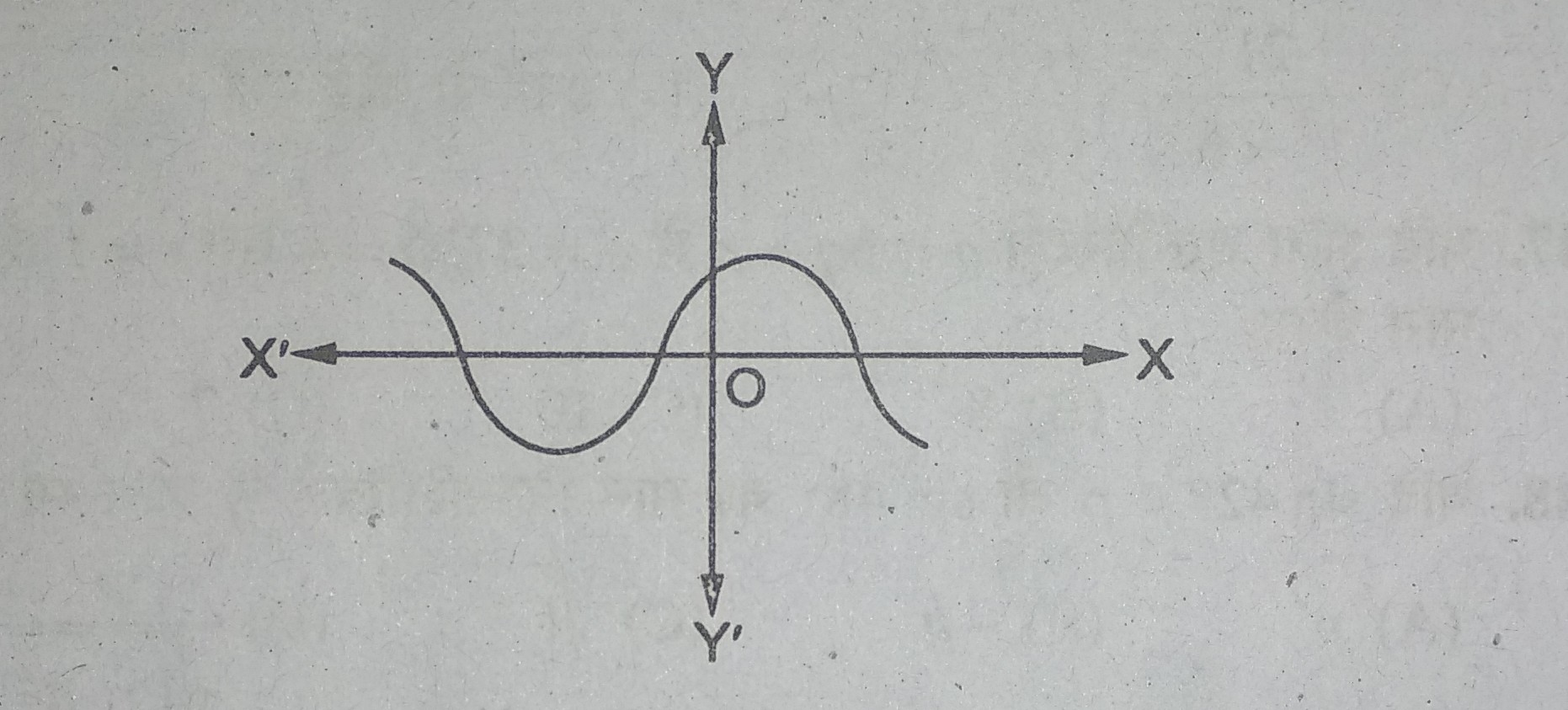
(A) 1
(B) 2
(C) 3
(D) 4
34. sin2 65° + sin2 25° का मान है
(A) 1
(B) 2
(C) 3
(D) -1
35. tan 5° · tan 13° · tan 77° · tan 85° का मान है
(A) 1
(B) 0
(C) -1
(D) इनमें से कोई नहीं
36. निम्नलिखित में से कौन tan 30° के बराबर है?
(A) tan 60°
(B) cot 60°
(C) cot 30°
(D) tan 15°
37. यदि 5 cot θ = 3 तब 5 sin θ – 3 cos / 4 sin θ + 3 cos θ का मान है
(A) 11/18
(B) 16/29
(C) 14/7
(D) 11/29
38. tan π/2 का मान है
(A) 0
(B) 1
(C) √3
(D) ∞
39. बिन्दु (√2, √3) की दूरी मूल बिन्दु से क्या होगी ?
(A) 2
(B) 4
(C) √3
(D) √5
40. x – अक्ष से बिन्दु Q ( 3, 6) की दूरी है
(A) 3 इकाई
(B) 6 इकाई
(C) 9 इकाई
(D) 3√5 इकाई
41. (cosec θ – cot θ)2 का मान क्या है
(A) 1 + cos θ / 1 – cos θ
(B) 1 – cos θ / 1 + cos θ
(C) 1 + sin θ / 1 – sin θ
(D) sin θ · cos θ
42. यदि एक शंकु की ऊँचाई h और आधार की त्रिज्या r है तो इसका आयतन होगा
(A) 1/3πrh
(B) 1/3πr2 h
(C) 1/3πrh2
(D) πr2h
43. यदि समान्तर श्रेणी का प्रथम पद ‘a’, सार्व अन्तर ‘d’ हो तो इसके प्रथम ‘n’ पदो का योगफल होगा
(A) a + (n – 1)d
(B) a + nd
(C) n/2 [2a + (n – 1)d]
(D) n/2[2a + nd]
44. एक घड़ी के मिनट वाली सुई द्वारा 60 मिनट में उसके केन्द्र द्वारा बनाया है
(A) 60°
(B) 120°
(C) 180°
(D) 360°
45. सामांतर श्रेणी 126, 120, 114, … का कौन-सा पद शून्य है ?
(A) 20वाँ
(B) 21 वाँ
(C) 22वाँ
(D) 23वाँ
46. 0.105 का p / 2n x 5m रूप निम्नलिखित में कौन है ?
(A) 12 / 22 x 5°
(B) 21 / 22 x 52
(C) 21 / 22 x 53
(D) इनमें से कोई नहीं
47. यदि भाग एल्गोरिद्म a = bq + r में a = 37, b = 4 एवं r = 1 तो q का मान होगा
(A) 9
(B) 8
(C) 10
(D) 7
48. यदि sin 42° = p तो sin 48° का मान निम्नलिखित में कौन-सा है ?
(A) p
(B) -p
(C) √1 – p2
(D) p/√1 – p2
49. यदि x2 + 1/x2 = 14 हो तो x + 1/x का मान होगा
(A) 3
(B) 4
(C) 5
(D) -2
50. ΔABC में, भुजा AB एवं AC पर क्रमश: D एवं E बिन्दु है। यदि DE || BC, AD = 4, DB = x – 4, AE = 8 तथा EC = 3x – 19, तो x का मान होगा
(A) 12
(B) 9
(C) 10
(D) 11
51. y – 4 = 0 का आलेख कैसी सरल रेखा होगी ?
(A) x-अक्ष के सामान्तर
(B) y-अक्ष के सामान्तर
(C) मूल बिन्दु से जाती हुई
(D) इनमें से कोई नहीं
52. यदि बहुपद x2 – 3( x + 1) – 5 के शून्यक α, β हों तो (α + 1) (β + 1) का मान होगा
(A) 3
(B) – 3
(C) – 4
(D) 4
53. यदि α एवं β द्विघात समीकरण x2 – 3√3x – 12 = 0 के मूल हों तो α + β – √3 का मान होगा
(A) 3√3
(B) – 4/3
(C) 2√3
(D) 4√3
54. यदि किसी त्रिभुज के शीर्षों के नियामक (0, 8), (0, 0) तथा (6,0) है, तो त्रिभुज का परिमाप होगा
(A) 14 इकाई
(B) 28 इकाई
(C) 24 इकाई
(D) 100 इकाई
55. बिन्दुओं (6, 5) एवं (–2, 11) को जोड़ने वाले रेखाखंड के मध्य बिन्दु का नियामक यदि (2, p) हो तो p का मान होगा
(A) 2
(B) 3
(C) -3
(D) 4
56. यदि किसी समान्तर श्रेणी का प्रथम पद 13 एवं सार्वअन्तर – 4 हो, इसके प्रथम 10 पदों का योगफल होगा तो
(A) 50
(B) – 50
(C) 30
(D) – 30
57. यदि समीकरण 3x2 – 10x + 3 = 0 का एक मूल 1/3 है तो दूसरा मूल होगा
(A) -1/3
(B) 1/3
(C) -3
(D) 3
58. sin(45° + θ) –cos (45° – θ) का मान क्या होगा ?
(A) 2 sin θ
(B) 2 cos θ
(C) 0
(D) 1
59. यदि जीवा AB वृत्त के केन्द्र पर 60° का कोण अंतरित करता है तो A और B बिन्दुओं पर खींची गई स्पर्श रेखाओं के बीच का कोण होगा
(A) 30°
(B) 60°
(C) 90°
(D) 120°
60. यदि A, B, C किसी त्रिभुज के कोण हों, तो sin(B + C / 2) बराबर है
(A) tan A / 2
(B) sin A/2
(C) cos A/2
(D) sec A/2
प्रश्न- दो पात्रों में 504 लीटर और 735 लीटर दूध है। पात्र की महत्तम धारिता क्या होगी, जो दोनों पात्रों के दूध को पूर्ण रूप से माप सके ?
उत्तर– दो पात्रों में क्रमश: 504 लीटर एवं 735 लीटर दूध है।
504)735(1
504
———
231)504(2
462
———
42)231(5
210
———
21)42(2
42
——
xx
504 और 735 का म०स० = 21
∴ पात्र की महत्तम धारिता = 21 लीटर; Ans. 2.
प्रश्न- सिद्ध करे कि √3 एक अपरिमेय संख्या है।
उत्तर– माना कि √3 एक परिमेय संख्या है।
∴ √3= a/b
जहाँ ‘a’ और b एक पूर्णांक है और a और b में कोई उभयनिष्ठ गुणनखंड नहीं है ।
दोनों ओर वर्ग करने पर, 3 = a2 / b2 ⇒ a2
∴ a2 , 3 से विभाज्य है।
∴ a भी 3 से विभाज्य होगा।
माना कि a = 3m, जहाँ m एक पूर्णांक है।
समीकरण (i) से, 3b2 = a2 ⇒ 3b2 = (3m)2
⇒ 3b2 = 9m2 ⇒ b2 = 3m2
∴ b2 , 3 का एक गुणज है।
∴ 3, b का एक गुणनखंड होगा।
इस प्रकार हम पाते हैं कि ‘a’ एवं ‘b’ का उभयनिष्ठ गुणनखंड 3 है। जो कि एक विरोधाभाष है।
∴ हमारी मान्यता गलत हुई ।
अतः √3 एक अपरिमेय संख्या होगी।
प्रश्न- यदि α, β बहुपद p ( x ) = x2 – 7x + k के शून्यक हैं और α – β = 1 है, तो k का मान ज्ञात करें।
उत्तर– बहुपद p(x) =x2 – 7x + k
∴ α + β = -b / a = (-7)/1 तथा αβ = c / a = k / 1 = k
∴ α + β = 7
एवं α – β = 1
∴ 2α = 8 या α = 4
अब समीकरण (i) से, α +β = 7 ⇒ 4 + β = 7 ∴ β = 3
∴ αβ = k ⇒ 4 × 3 = k ∴ k =12; Ans.
प्रश्न- एक द्विघातीय बहुपद ज्ञात करें जिसके शून्यकों का योगफल एवं गुणनफल क्रमश: 4 एवं 1 है।
उत्तर– माना कि द्विघात बहुपद = ax2 + bx + c के मूल α एवं β हैं।
∴ α + β = 4, αβ = 1
अतः द्विघात बहुपद = x2 – (α + β) x + αβ = x2 – 4x + 1; Ans.
प्रश्न- दो संख्याओं का अन्तर 26 है तथा एक संख्या, दूसरी संख्या की तीन गुनी है। दोनों संख्याएँ ज्ञात करें।
उत्तर– माना कि दो अभीष्ट संख्याएँx एवं y हैं जहाँ x > y
प्रश्नानुसार, x – y = 26 x …(i)
एवं. x = 3y
अब x का मान समीकरण (i) में रखने पर,
3y – y = 26 ⇒ 2 y = 26 ∴ y =13
∴ x = 3y = 3 ×13 = 39.
अतः दो अभीष्ट संख्याएँ 13 एवं 39 हैं।
प्रश्न- दो अनुपूरक कोणों का अन्तर 22° है। उनकी माप ज्ञात करें।
उत्तर– माना कि दो अनुपूरक कोण x एवं y हैं, तथा x > y है।
चूँकि दो अनुपूरक कोणों का योग 90° होता है।
∴ x + y = 90° …(i)
तथा प्रश्नानुसार, x – y = 22 … (ii)
समीकरण (i) एवं (ii) को जोड़ने पर, हम पाते हैं कि
2x = 112° ∴ x = 112° / 2 = 56°
समीकरण (i) में x का मान रखने पर,
x + y = 90° ⇒ 56° + y = 90°
∴ y = 90° = 56° = 34°
अतः दो अनुपूरक कोण 56° एवं 34° है ।
प्रश्न- हल करें — √13 – x2= x + 5
उत्तर– √13 – x2 = x + 5
दोनों ओर वर्ग करने पर,
13 – x2 = (x + 5)2
⇒ 13- x2 = x2 + 10x + 25
⇒ x2 + 10x + 25 + x2 – 13 = 0
⇒ 2x2 + 10x + 12 = 0
⇒ x2 + 5x + 6 = 0
⇒ x2 + 3x + 2x + 6 = 0
⇒ x(x + 3) + 2 (x + 3) = 0
⇒ (x + 2) (x + 3) = 0
∴ x = -2 या -3; Ans
प्रश्न- एक संख्या और उसके व्युत्क्रम का योग 10 / 3 है। संख्या ज्ञात करें ।
उत्तर– मान लिया कि अभीष्ट संख्या x है।
अतः इसका व्युत्क्रम = 1 / x
अब प्रश्नानुसार, x + 1 / x = 10 / 3 ⇒ x2 + 1 / x = 10 / 3
⇒ 3x2 + 3 = 10x
⇒ x2 – 10x + 3 = 0
⇒ 3x2 – 9x – x + 3 = 0
⇒ 3x(x – 3) – 1 (x – 3) = 0
⇒ (x – 3) (3x – 1) = 0
⇒ x = 3 या 1 / 3
अत: अभीष्ट संख्या 3 या 1 / 3 होगी।
प्रश्न- एक समांतर श्रेणी में, a = 5, d = 3 और Tn = 50 है। ‘n’ एवं Sn का मान ज्ञात करें।
उत्तर– दिया गया है कि a = 5, d = 3 एवं Tn = 50, n = ? Sn = ?
∴ Tn = a + (n – 1)d
⇒ 50 = 5 + (n – 1)3
⇒ n – 1 = 50 – 5 / 3 = 45 / 3 = 15
∴ n = 15 + 1 = 16; Ans
∴ Sn = n/2 [2a + (n – 1)d]
∴ S16 = 16/2 [2 x 5 + (16 – 1)3]
= 8[10 + 15 x 3] = 8[10 + 45]
= 8 x 55 = 440
∴ S16 = 440 Ans.
प्रश्न- उस समांतर श्रेणी का 31वाँ पद ज्ञात करें जिसका 11वाँ पद 38 है और 16वाँ पद 73 है।
उत्तर– दिया गया है कि T11 = 38, T16 = 73, T31 = ?
चूँकि T11 = 38 ⇒ a + 10d = 38
एवं T16 = 73 ⇒ a + 15d = 73
समीकरण (ii) में से समीकरण (i) को घटाने पर,
a + 15d = 73
a + 10d = 38
– – –
———————
5d = 35 ∴ d = 35/5 = 7
अब, d का मान समीकरण (i) में रखने पर,
a + 10d = 38 ⇒ a + 10 x 7 = 38
⇒ a + 38 – 70 = -32
अब T31= a + 30d
= -32 + 30 x 7 = -32 + 210 = 178
∴ T31 = 178; Ans
प्रश्न- किसी त्रिभुज के तीन कोण x, y तथा 40° हैं। दो कोण x और y के बीच का अन्तर 30° है। x और y का मान ज्ञात करें ।
उत्तर– दिये गये त्रिभुज के तीनों कोण हैं क्रमश: x, y एवं 40° हैं।
चूँकि त्रिभुज के तीनों कोणों का योगफल 180° होता है।
∴ x + y + 40 = 180°
⇒ x + y =140°
तथा दिया गया है कि x – y = 30°
समीकरण (i) एवं (ii) को जोड़ने पर,
2x = 170° ∴ x = 85°
अब समीकरण (i) में x का मान रखने पर,
x + y =140° ⇒ 85° + y = y = 140°
∴ y = 140° – 85° = 55°
इस प्रकार, x = 85°, y = 55°; Ans.
प्रश्न- दिये गये चित्र में AC ⊥ BD तथा CE ⊥ AD है। सिद्ध करें कि AC2 = DA · AE
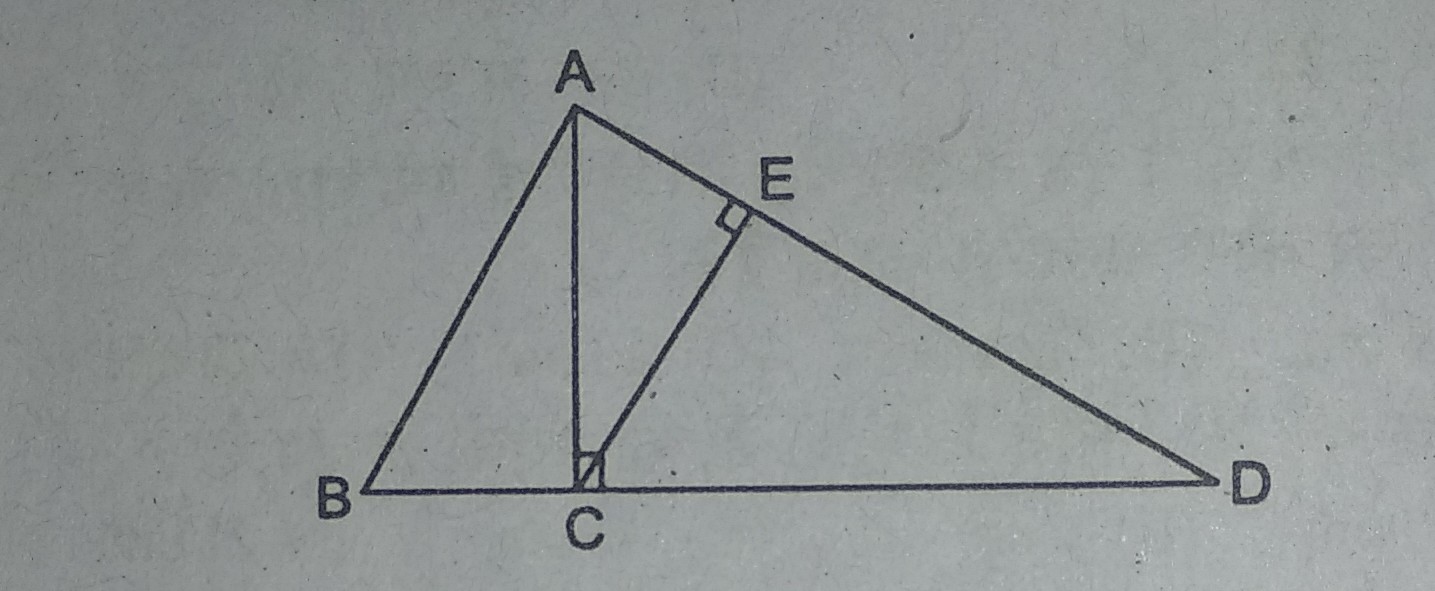
उत्तर– ΔABD में, AC ⊥ BD, CE ⊥ AD
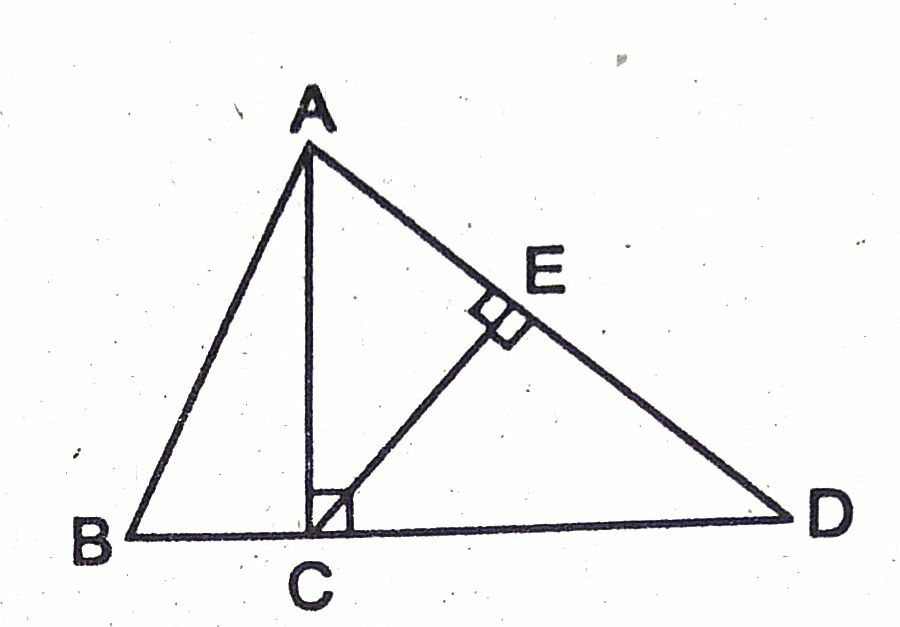
सिद्ध करना है— AC2 = DA · AE
प्रमाण— ΔACE तथा ΔACD में
∠AEC = ∠ACD
∠CAD = ∠CAE (उभयनिष्ठ)
∴ ΔACE ~ ΔACD (AA समरूपता से)
अतः इसकी संगत भुजाएँ समानुपाती होंगी।
∴ AC / AD = AE / AC ⇒ AD · AE = AC2
= AC2 = AD · AE; Proved.
प्रश्न- त्रिभुज ABC के अन्दर एक वृत्त है, जो भुजाओं AB, BC एवं AC को क्रमशः D, E एवं F बिन्दुओं पर स्पर्श करता है। यदि AB = 12 cm, BC = 8 cm एवं AC = 10cm हो, तो AD, BE एवं CF की लम्बाई ज्ञात करें।
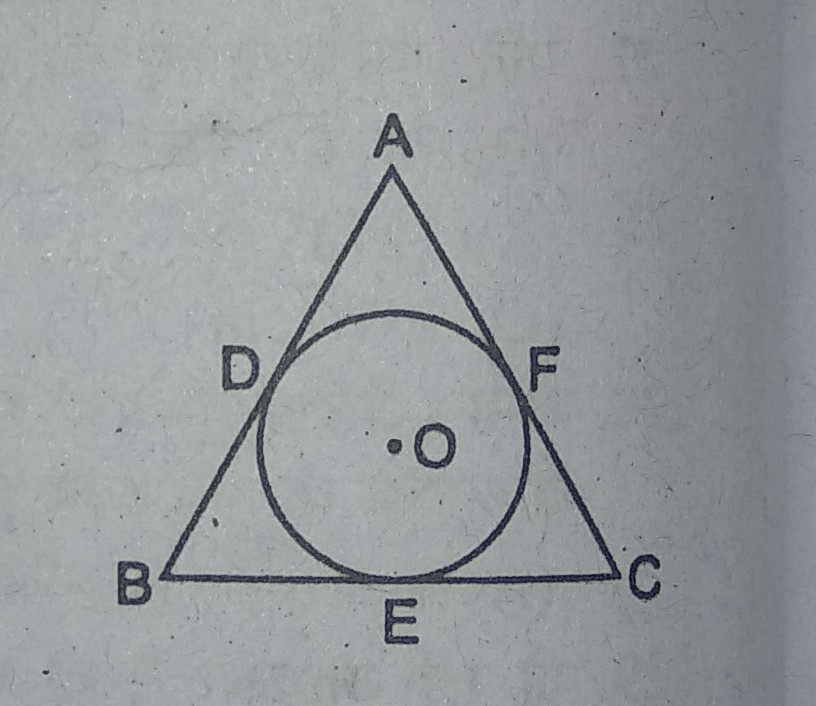
उत्तर– दिया गया है कि AB = 12cm, BC = 8cm एवं AC = 10cm है ।
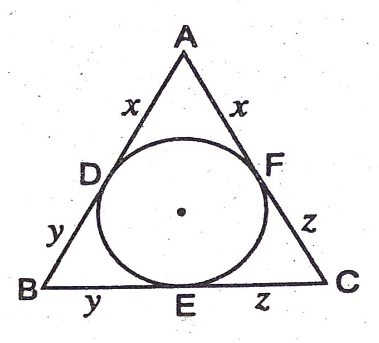
ज्ञात करना है – AD, BE एवं CF
प्रमाण— माना कि AD = x सेमी
चूँकि बाह्य बिन्दु से वृत्त पर खींची स्पर्श रेखाएँ समान होती हैं।
∴ AD = AF = x
इसी प्रकार BE = BD = y (माना)
एवं CE = CF = z (माना)
अब, ΔABC में, AB + BC + AC =(12 + 8 + 10)cm = 30cm
⇒ x + y + y + z + z + x = 30
⇒ 2(x + y + z) = 30
⇒ x + y + z = 15
अतः x = (x + y + z) – (y – z)
⇒ AD = 15 – BC = 15 – 8 = 7cm
y = (x + y + z) – (z + x)
⇒ BE = 15 – AC = 15 – 10 = 5cm
एवं z = (x + y + z) – (x + y)
⇒ CF = 15 – AB = 15 – 12 = 3cm
अतः AD = 7cm, BE = 5cm, CF = 3cm; Ans
प्रश्न- यदि sin 3A = cos (A- 26°), जहाँ 3A एक न्यूनकोण है, तो A का मान ज्ञात करें।
उत्तर– sin 3 A = cos(A – 26°)
⇒ cos(90° – 3A) = cos(A – 26°) [:: cos (90° – A) = sinA
⇒ 90° – 3A = A – 26°
⇒ 90° + 26° = 3A + A
⇒ 116° = 4A ∴ A = 116/4 = 29°; Ans
प्रश्न- सिद्ध करें कि sin4θ – cos4 / sin2 θ – cos2 θ = 1.
उत्तर– L.H.S = sin4 θ – cos4 θ / sin2 θ – cos2 θ = (sin2 θ)2 – (cos2 θ)2
= (sin2 θ – cos2 θ) (sin2 θ – cos2 θ) / (sin2 θ – cos2 θ)
[∴ a2 – b2 = (a + b) (a – b)]
= sin2 θ+ cos2 θ= 1 = R.H.S.; Proved.
प्रश्न- यदि बिन्दुएँ (3, 3), (a, 0) और (0, b) संरेखी है, तो सिद्ध करें कि 1 / a + 1 / b = 1 / 3
उत्तर– चूँकि दी गई बिन्दुएँ A (3, 3), B (a, 0) एवं C (0, b) संरेखी हैं।
सिद्ध करना है— 1 / a + 1 / b + = 1 / 3
प्रमाण— यहाँ पर x1 = 3, y, = 3, x2 = a, y2 = 0
एवं x3 = 0, y3 = b
चूँकि A, B एवं C संरेखी है ।
∴ x1 (y2– y3) + x2(y3 – y1) + x3 (y1 – y2) = 0
⇒ 3(0 – b) + a(b – 3) + 0(3 – 0) = 0
⇒ ab = 3a + 3b
⇒ ab = 3(a + b)
अब दोनों ओर ab से भाग देने पर,
ab / ab = 3(a + b) / ab ⇒ 1 / 3 = a + b / ab = a / ab + b / ab
⇒ 1 / 3 = 1 / b + 1 / a अर्थात् 1 / a + 1 / b = 1 / 3; Proved.
प्रश्न- उस त्रिभुज का केन्द्रक निकालें जिनके शीर्ष (3, – 5), (– 7, 4) तथा (10, – 2) है।
उत्तर– त्रिभुज ABC के केन्द्रक का निर्देशांक
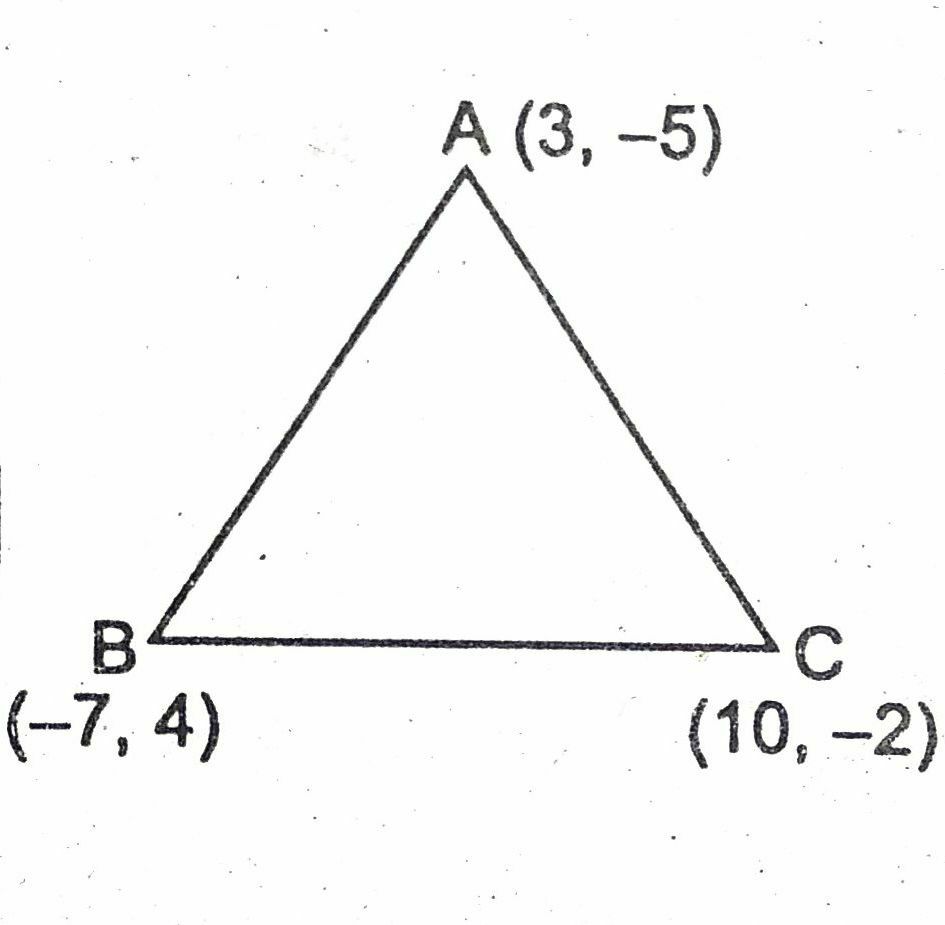
= [x1+ x2 + x3 / 3, y1 + y2 + y3 / 3]
= [3+ (-7) + 10 / 3, -5 + 4 + (-2) / 3]
= [3 – 7 + 10 / 3, 4 – 5 -2 / 3]
= [6/3, 4 – 7 / 3] = 2 -3/3
= (2, -1); Ans
प्रश्न- एक तार वृत्त के रूप में है जिसकी त्रिज्या 84 सेमी है। उस वर्ग का क्षेत्रफल ज्ञात करें जो तार को मोड़ कर बनाया जा सकता है।
उत्तर–
वृत्त की त्रिज्या = 84 cm
∴ वृत्त की परिधि = 2 πr
= 2 x 22/7 x 84
= 2 x 22 x 12 = 528cm
चूँकि तार को मोड़कर एक वर्ग बनाया जाता है।
वर्ग का परिमाप = वृत्त की परिधि = 528cm
∴ वर्ग की एक भुजा = परिमाप / 4 = 528 / 4 = 132cm
∴ वर्ग का क्षेत्रफल = (भुजा)2 = (132 cm)2 = 132 cm
= 17424 cm2; Ans.
प्रश्न- किसी वृत्त के एक त्रिज्यखंड का परिमाप 29 सेमी है। यदि वृत्त की त्रिज्या 6.5 सेमी हो, तो त्रिज्यखंड का क्षेत्रफल ज्ञात करें ।
उत्तर–
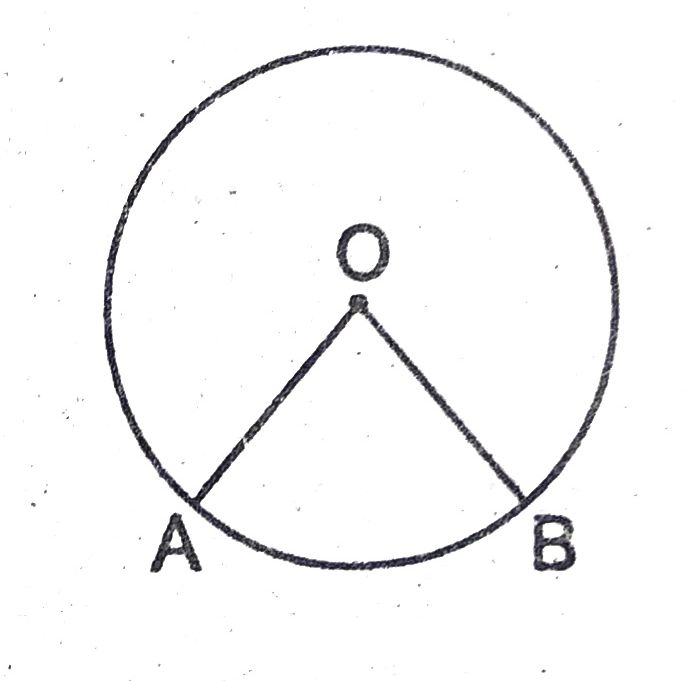
त्रिज्यखंड का परिमाप = 29 cm
त्रिज्या = 6.5cm
चूँकि त्रिज्यखंड की परिमाप = l + 2r
[∴ l = चाप की लम्बाई है।
⇒ 29cm =l + 2 x 6.5cm
= 29cm = l + 13cm
∴ l = (29 – 13)cm = 16cm.
∴ त्रिज्यखंड का क्षेत्रफल = 1 / 2 x चाप की लम्बाई x त्रिज्या
= 1/2 x 16cm x 6.5cm
= 8cm x 6.5cm = 52.0cm2 ; Ans
प्रश्न- ताँबे के एक ठोस गोले का व्यास 6 cm है, को पिघलाकर समान अनुप्रस्थ काट वाले तार के रूप में परिणत किया जाता है। यदि तार की लम्बाई 36cm हो, तो तार की त्रिज्या ज्ञात करें।
उत्तर– गोले की त्रिज्या (R) = 6 / 2 = 3cm
अतः गोले का आयतन = 4 / 3πr3 = 4/3 π x 3 x 3 x 3 = 36πcm3
चूकि तार की लम्बाई (h) = 36 cm है।
माना कि तार की त्रिज्या = r cm
∴ तार का आयतन = πr2h = π · r2 x 36 = 36 πr2 cm3
प्रश्नानुसार, तार का आयतन = गोले का आयतन
⇒ 36πr2 = 36π = r2 = 1 ∴ r = 1cm
तार की त्रिज्या = 1 सेमी; Ans.
प्रश्न- एक लम्बवृत्तीय शंकु का आयतन 100 πcm3 है और ऊँचाई 12 cm है, तो शंकु की तिर्यक ऊँचाई ज्ञात करें ।
उत्तर– दिया गया है कि शंकु का आयतन = 100r cm3, ऊँचाई = 12 cm
∴ शंकु का आयतन = 100π
⇒ 1/3πr2h = 100π ⇒ 1/3r2h = 100
⇒ 1/3r2 x 12 = 100 = r2 = 3 x 100 / 12 = 25 ∴ r = 5cm
अतः शंकु की तिरछी ऊँचाई ( l ) = √r2 + h2 = √52 + 122
= √25 + 144 = √169 = 13cm
∴ शंकु की तिरछी ऊँचाई = 13 cm; Ans.
प्रश्न- दिये गए बारंबारता बंटन का बहुलक ज्ञात करें।
| वर्ग अन्तराल | 10 – 25 | 20 – 40 | 40 – 55 | 55 – 70 | 70 – 85 | 85 – 100 |
| बारंबारता | 2 | 3 | 7 | 6 | 6 | 6 |
उत्तर–
| वर्ग अन्तराल | बारंबारता |
| 10 – 25 | 2 |
| 25 – 40 | 3 |
| 40 – 55 | 7 |
| 55 – 70 | 6 |
| 70 – 85 | 6 |
| 85 – 100 | 6 |
चूँकि वर्ग अन्तराल (40-55) की बारंबारता सर्वाधिक है।
∴ माध्यिका वर्ग = 40 – 55
∴ l = 40, f0 = 7, f-1 = 3, f-2 = 6, h = 15
बहुलक = l + f0 – f-1 / 2f0 – f-1 – f-2 x h = 40 + 7 – 3 / 2 x 7 – 3 – 6 x 15
= 40 + 4 / 14 – 9 x 15 = 40 + 4 / 5 x 15 = 40 + 12 = 52; Ans
प्रश्न- दिये गए आँकड़ों का माध्य 18 है, तो अज्ञात बारंबारता ज्ञात करें।
| वर्ग अन्तराल | 11-13 | 13-15 | 15-17 | 17-19 | 19-21 | 21-23 | 23-25 |
| बारंबारता | 7 | 6 | 9 | 13 | f | 5 | 4 |
उत्तर–
| C.I | f | xi | fixi |
| 11 – 13 | 7 | 12 | 84 |
| 13 – 15 | 6 | 14 | 84 |
| 15 – 17 | 9 | 16 | 144 |
| 17 – 19 | 13 | 18 | 234 |
| 19 – 21 | f | 20 | 20f |
| 21 – 23 | 5 | 22 | 110 |
| 23 – 25 | 4 | 24 | 96 |
| ∑fi = 44 + f | ∑fixi = 752 + 20f |
माध्य = ∑fix / ∑fi ⇒ 18 = 752 + 20f / 44 + f
⇒ 752 + 20f = 792 + 18f = 20f – 18f = 792 – 752
⇒ 2f = 40 ∴ f = 40 / 2 = 20; Ans
प्रश्न- 20 बल्वों के एक समूह में 4 बल्व खराब हैं। इस समूह में से एक बल्व यादृच्छया निकाला जाता है। इसकी क्या प्रायिकता है कि बल्व खराब होगा ?
उत्तर– दिये गए कुल बल्वों की संख्या = 20
खराब बल्वों की संख्या =4
∴ अनुकूल परिणामों की संख्या = 4
∴ खराब बल्ब की प्रायिकता P(E) = 4 / 20 = 1 / 5; Ans
प्रश्न- एक थैले में 5 लाल एवं कुछ नीली गेंद है। यदि नीली गेंद को निकालने की प्रायिकता लाल गेंद को निकालने की प्रायिकता से दुगुनी हो, तो थैले में रखे नीली गेंदों की संख्या क्या होगी ?
उत्तर– थैले में लाल गेंदों की संख्या = 5
मान लिया की नीली गेंदों की संख्या x है।
∴ थैले में गेदों की कुल संख्या = (5+x)
अतः नीली गेंद की प्रायिकता = x / 5 + x
एवं लाल गेंद की प्रायिकता = 5 / 5 + x
प्रश्नानुसार, नीली गेंद की प्रायिकता = 2x लाल गेंद की प्रायिकता
⇒ π / 5 + x = 2 x 5 / 5 + x ⇒ x = 2 x 5 = 10
∴ थैले में नीली गेंद की संख्या = 10; Ans.
प्रश्न- सिद्ध करें कि किसी समकोण त्रिभुज में कर्ण का वर्ग, उसके अन्य दो भुजाओं के वर्गों के योगफल के बराबर होता है।
उत्तर–
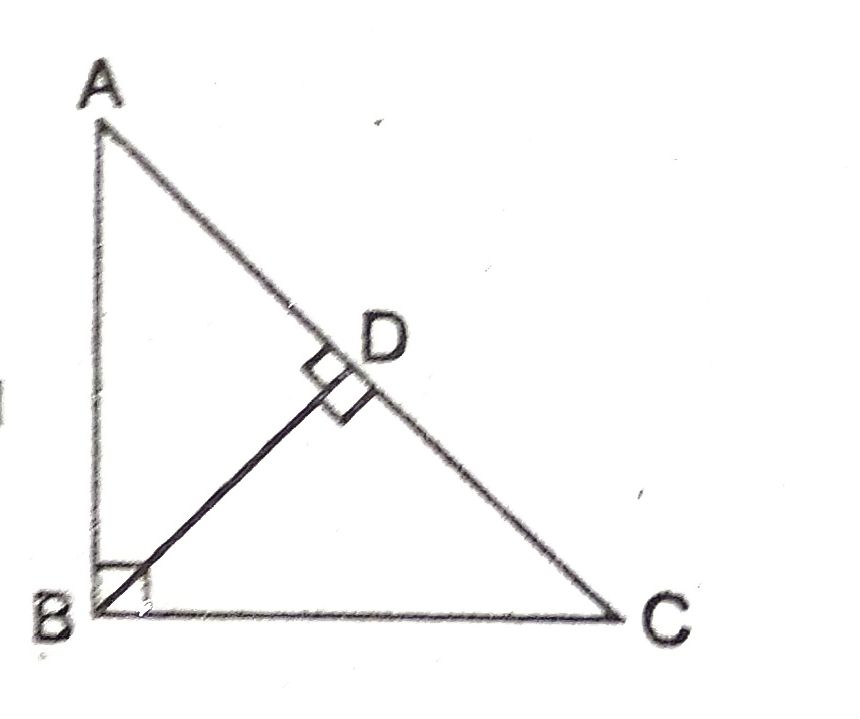
दिया है— ABC एक समकोण त्रिभुज है जिसमें ∠B = 90° है।
सिद्ध करना है— AC2 = AB2 + BC2
रचना— B से AC पर AD लम्ब डाला गया।
प्रमाण— ΔABC एवं ΔADB में,
∠BAC = ∠BAD (उभयनिष्ठ)
∠ABC = ∠ADB = 90°
∴ ΔABC – ΔADB. (AA समरूपता से)
अतः दोनों त्रिभुजों की संगत भुजाएँ समानुपाती होंगी।
∴ AC / AB = AB / AD ⇒ AB2 = AC · AD
इसी प्रकार, ΔCBA एवं ΔCDB में,
∠BCA = ∠BCD (उभयनिष्ठ)
∠CBA = ∠CBD = 90°
∴ ΔCBA ~ ΔCDB (AA-समरूपता से)
∴ AC / BC = BC / DC
⇒ BC2 = AC · DC
अब समीकरण (i) एवं (ii) को जोड़ने पर,
AB2 + BC2 = AC · AD + AC · DC
= AC (AD + DC) = AC · AC = AC2
अतः AB2 + BC2 = AC2; Proved.
प्रश्न- एक झील के तल से h मीटर की ऊँचाई पर स्थित एक बिन्दु से देखने पर एक बादल का उन्नयन कोण α है तथा इसी बिन्दु से झील में बादल के प्रतिबिम्ब का अवनमन कोण β है। सिद्ध करें कि झील के तल से बादल की ऊँचाई h(tan β + tan α) / (tan β – tan α) होगी।
उत्तर–
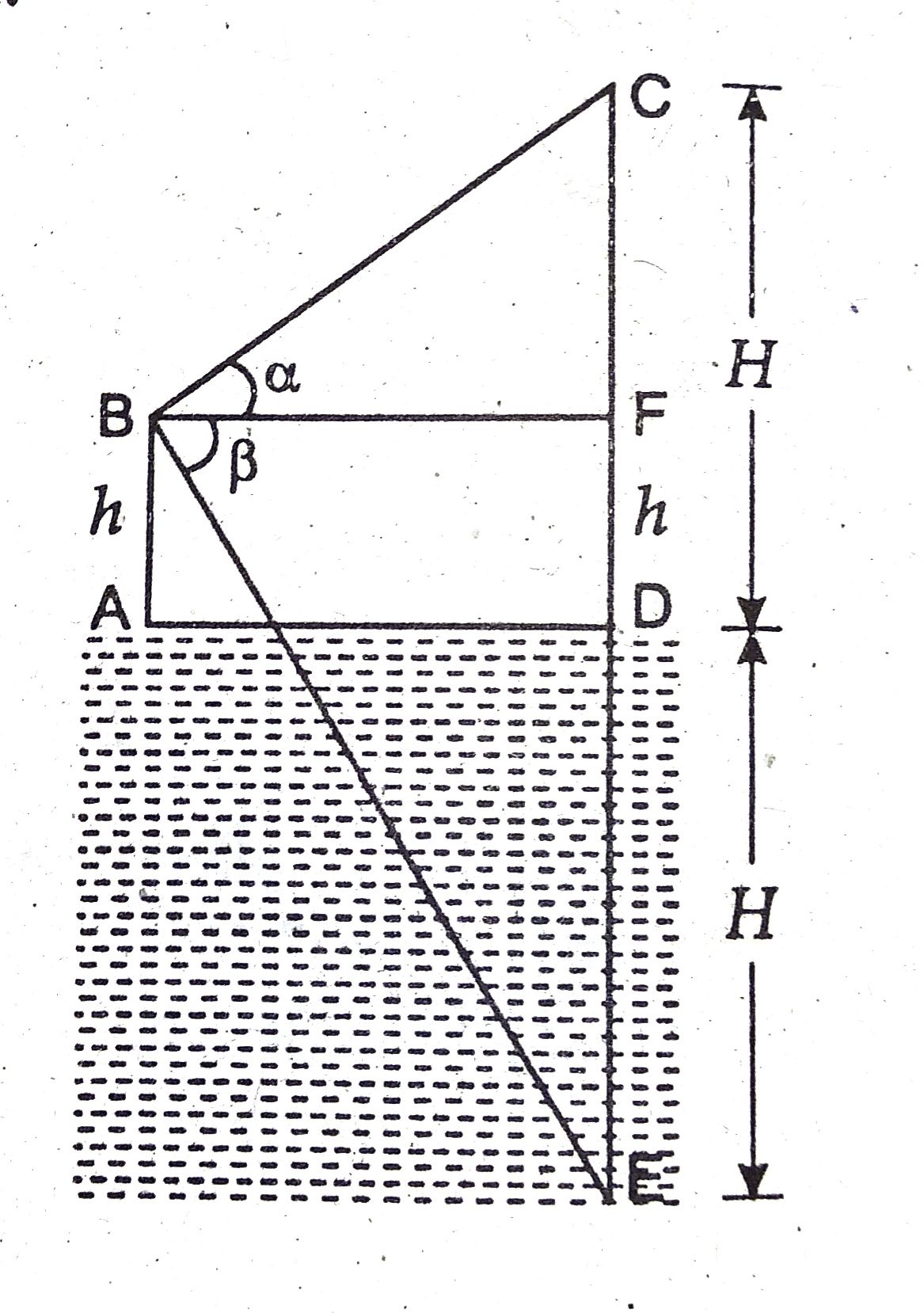
मानलिया कि AD झील की सतह है
तथा बिन्दु A के लम्बवत् ऊपर एक बिन्दु B
इस प्रकार है कि AB = h मी
माना कि बिन्दु ‘C’ बादल की स्थिति
है, तथा बिन्दु E, बादल का प्रतिबिम्ब है।
B से BF ⊥ CE खींचा।
मानलिया कि DC = H = DE
∴ AB = DF = h
∴ CF = CD – DF = H – h
एवं EF = DE + DF = H + h
अब समकोण ΔBCF में,
tan α = CF / BF = H – h / BF
∴ BF = H – h / tan α
इसी प्रकार समकोण ΔBFE में
tan β = EF/BF = H – h/BF ∴ BF = H + h/tan β
अतः समीकरण (i) एवं (ii) से, H – h / tan α = H + h/tan β
⇒ H tan β – h tan β = H tan α + h tan α
⇒ H tan β – H Tan α = h tan β+ h tan α
⇒ H(tan β – tan α) = h(tan β + tan α)
∴ H= h(tan β + tan α) / (tan β – tan α)
अतः झील के तल से बादल की ऊँचाई
h(tan β + tan α)/ ( tan β – tan α ); Proved.
प्रश्न- किसी समान्तर श्रेणी का pवाँ पद – एवं q वाँ पद 1/p है। सिद्ध करें कि इसके pq पदों का योगफल 1/2 (pq + 1) होगा।
उत्तर– मानलिया कि दी गई A.P. का प्रथम पद ‘a’ एवं सार्वअन्तर ‘d ‘ है।
∴ Tn = a + (n – 1)d
∴ Tp = a + (p – 1)d
∴ Tp = 1 / q ∴ a + (p – 1)d = 1 / p
इसी प्रकार, Tq = 1 / q ∴ a (q – 1)d = 1 / p
अब समीकरण (i) में से समीकरण (ii) को घटाने पर,
(P – 1)d – (q – 1)d = 1/q – 1/p
⇒ d(p – 1 – q + 1) = p – q / pq ∴ d = 1 / pq
⇒ d(p – q) = (p – q) / pq ∴ d = 1 / pq
समीकरण (i) में d का मान रखने पर,
a + (p – 1)d = 1 / q ⇒ a + (p – 1) 1 / pq = 1 / pq
अब, Sn = n / 2 [2a + (n – 1)d]
∴ Spq = pq / 2 [2 x 1 / pq + (pq – 1) 1 / pq]
= Pq/q [2/pq + pq – 1 / pq]
= pq / 2 [2 + pq – 1 / pq] = pq / 2 x pq + 1 / pq = 1 / 2(pq + 1)
अतः दी गई श्रेणी के pq पदों का योगफल = 1 / 2 (pq + 1); Ans
प्रश्न- एक हवाई जहाज अपने निर्धारित समय से 30 मिनट देर से उड़ान भरता है, तथा 1500km की दूरी निर्धारित समय में तय करने के लिए उसे अपनी चाल वास्तविक चाल से 250 km/h बढ़ानी पड़ती है। हवाई जहाज की वास्तविक चाल ज्ञात करें।
उत्तर– मानलिया कि हवाई जहाज की वास्तविक चाल = x km / h
तथा उसकी बढ़ी हुई चाल = (x + 250 ) km / h
अतः वास्तविक चाल से हवाई जहाज को 1500km की दूरी तय करने में लगा समय = 1500 / x + 250 घंटे
चूँकि नई चाल से लगा समय, वास्तविक चाल से लगे समय से 30 मिनट अर्थात् 1 / 2 घंटे कम है।
∴ 1500 / x = 1500 / 250 + x = 1 / 2
⇒ 1500 (250 + x) – 1500x / x(250 + x) = 1/2
⇒ 375000 + 1500x – 1500x / 250x + x2 = 1/2 ⇒ 375000 / x2 + 250x = 1 / 2
⇒ x2 + 250x = 750000
⇒ x2 + 250x – 750000 = 0
⇒ x2 + 1000x – 750x – 750000 = 0
⇒ x(x + 1000) – 750 (x + 1000) = 0
⇒ (x – 750) (x + 1000) = 0
∴ x = 750 या x = -1000
अतः हवाई जहाज की वास्तविक चाल = 750 km / h; Ans.
प्रश्न- एक समकोण त्रिभुज जिसकी समकोण बनाने वाली भुजाएँ 3 cm एवं 4cm हैं, को उसके कर्ण के परितः घुमाया जाता है। इस प्रकार प्राप्त द्विशंकु का आयतन एवं पृष्ठीय क्षेत्रफल ज्ञात करें।
उत्तर–
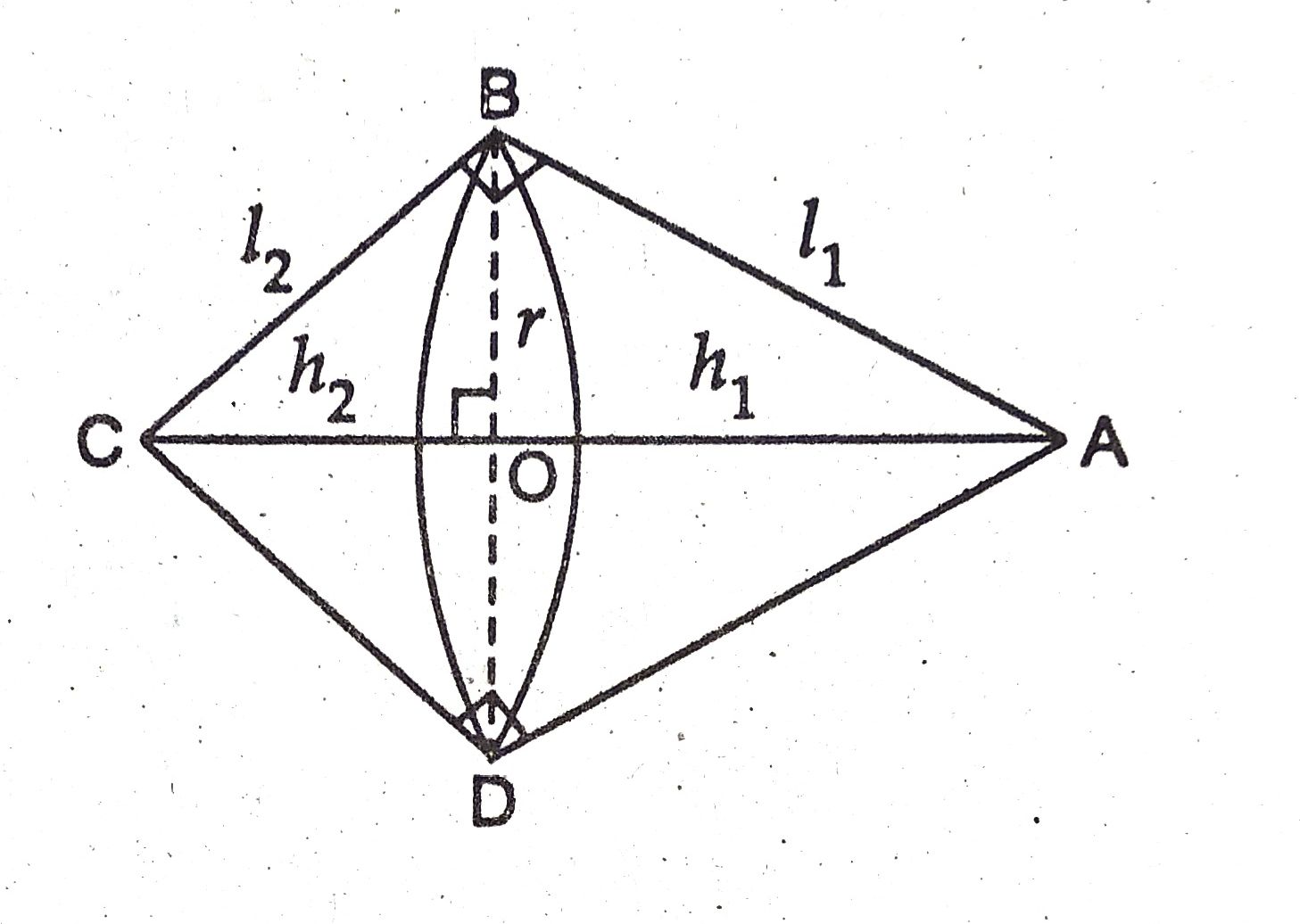
माना कि समकोण ΔABC में ∠B = 90° AB = 4 cm एवं BC = 3 cm, इसे इसके कर्ण के परितः घुमाने पर एक द्विशंकु ABCD प्राप्त होता है।
समकोण ΔABC में
AC2 = AB2 + BC2
= 42 + 32
= 16 + 9 = 25
∴ AC = 5cm
माना कि AB = I1 OA = h1 , BC = l2, OC = h2 तथा OB = r
∴ h1 + h2 = AC = 5cm
अब ΔABC का क्षेत्रफल 1/2 x BC x AB = 1/2 x 3 x 4 = 6cm3
पुन: ΔABC का क्षेत्रफल = 1/2 x AC x OB = 1/2 x 5 x r
अतः 1/2 x 5 x r = 6 :: r = 12/5 cm
अब द्विशंकु ABCD का आयतन = दोनों शंकुओं के आयतनों का योग
= 1/3 πr2 h1 + 1/3 πr2 h2 = 1/3 πr2 (h1 + h2)
= 1/3 x 22/7 x 12/5 x 5
= 22/21 x 144/5 x 3168/105 = 30.17cm3
अब द्विशंकु का पृष्ठीय क्षेत्रफल
= दोनों शंकुओं के वक्रपृष्ठीय क्षेत्रफलों का योगफल
= πrl1 + πrl2 = πr( l1 + l2) = 22/7 x 12/5 (4 + 3)
= 22/7 x 12/5 x 7 = 264/5 = 52.8cm2; Ans
प्रश्न- तीन शीर्ष बिन्दुओं A(k, 2k), B(−2, 6) एवं C(3, 1) से बने त्रिभुज का क्षेत्रफल 5 वर्ग इकाई है। k का मान ज्ञात करें।
उत्तर–
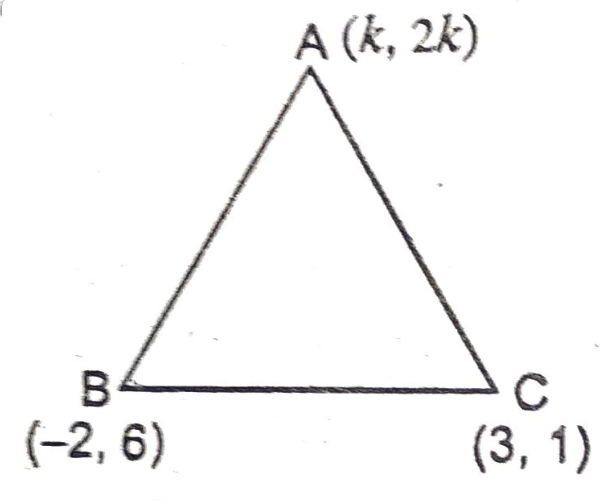
माना कि x1 = k, y1 = 2k
x1= -2, y2= 6
x3= 3, y3 = 1 है।
ΔABC के क्षेत्रफल
= 1/2 | [x1 (y2 – y3 ) + x2 (y3 – y1 ) + x3(y1 – y2 )]|
= 1/2 | [k(6 – 1) -2(1 – 2k) + 3 (2k – 6)]|
= 1/2 |[5k – 2 + 4k + 6k – 18]| = 1/2 |[15k – 20]|
चूँकि दिया गया है कि ΔABC का क्षेत्रफल 5 वर्ग इकाई है।
∴ 1/2 |[15k – 20]| = 5 = | 15k – 20 = -10
∴ 15k – 20 = 10 या 15k – 20 = -10
⇒ 15k = 20 + 10 या 15k = 20 – 10 = 10
⇒ 15k = 30 या k = 10/15
∴ k=2 या k = 2/3
इस प्रकार k = 2 या 2/3; Ans.
प्रश्न- 2.5 सेमी त्रिज्या का एक वृत्त खींचें। वृत्त के बाहर स्थित किसी बिन्दु P से वृत्त के केन्द्र का बिना उपयोग करते हुए वृत्त की दो स्पर्श रेखाएँ खीचें।
उत्तर– रचना के चरण—
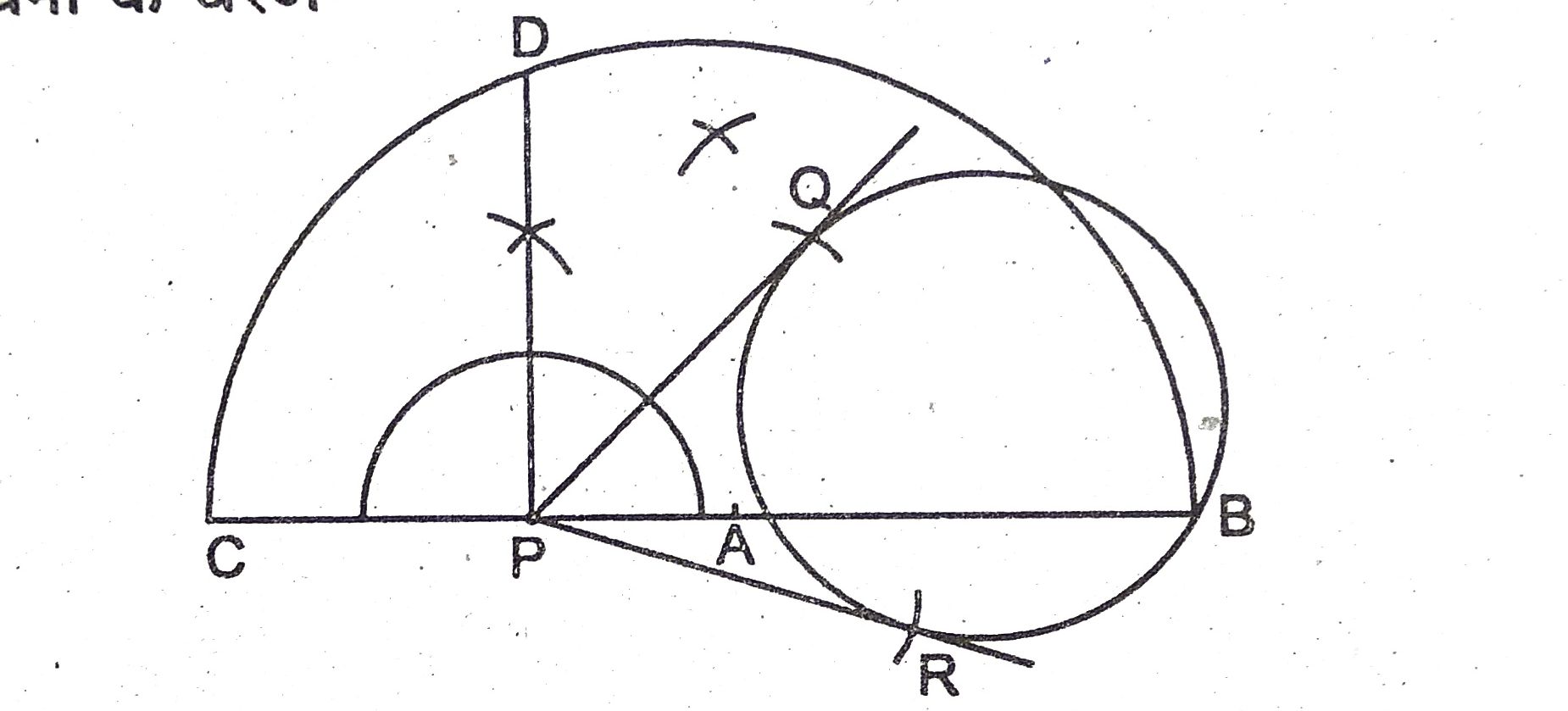
(i) 2.5 cm त्रिज्या का एक वृत्त खींचा एवं वृत्त के बाहर कोई बिन्दु P लिया।
(ii) P से वृत्त की एक छेदक रेखा PAB खींचा।
(iii) AP को बिन्दु C तक इस प्रकार बढ़ाया कि AP = PC
(iv) अब BC को व्यास लेते हुए एक अर्द्धवृत्त खींचा
(v) अब बिन्दु P पर एक लम्ब खींचा जो अर्द्धवृत्त को बिन्दु D पर
(vi) अब P को केन्द्र तथा PD को त्रिज्या लेकर अभीष्ट वृत्त पर दो चाप काटा जो वृत्त को Q एवं R पर काटता है।
(vii) PQ एवं PR को मिलाया। PQ एवं QR अभीष्ट वृत्त की दो स्पर्श रेखाएँ हैं।
प्रश्न- नीचे दिये गए समीकरण युग्मों को ग्राफीय विधि से हल करें—
4x – 5 y = 20
3x + 5y = 15
इन समीकरणों को निरूपित करने वाली रेखाओं एवं y- अक्ष के बीच बने त्रिभुज के शीर्ष बिन्दुओं के निर्देशांकों को लिखें।
उत्तर– दिया गया समीकरण है—
4x – 5y = 20 … (i); 3x + 5y = 15 …(ii)
समीकरण (i) से,
4x – 5y = 20 ⇒ 4x – 20 = 5y ∴ y = 4x – 20 / 5
दिये गए समीकरण का मान सारिणी
| x | 5 | 0 | -5 |
| y | 0 | -4 | -8 |
फिर समीकरण (ii) से,
3x + 5y = 15 ⇒ 5y – 3x ∴ y = 15 – 3x/5
मान सारिणी
| x | 5 | 0 | -5 |
| y | 0 | 3 | 6 |
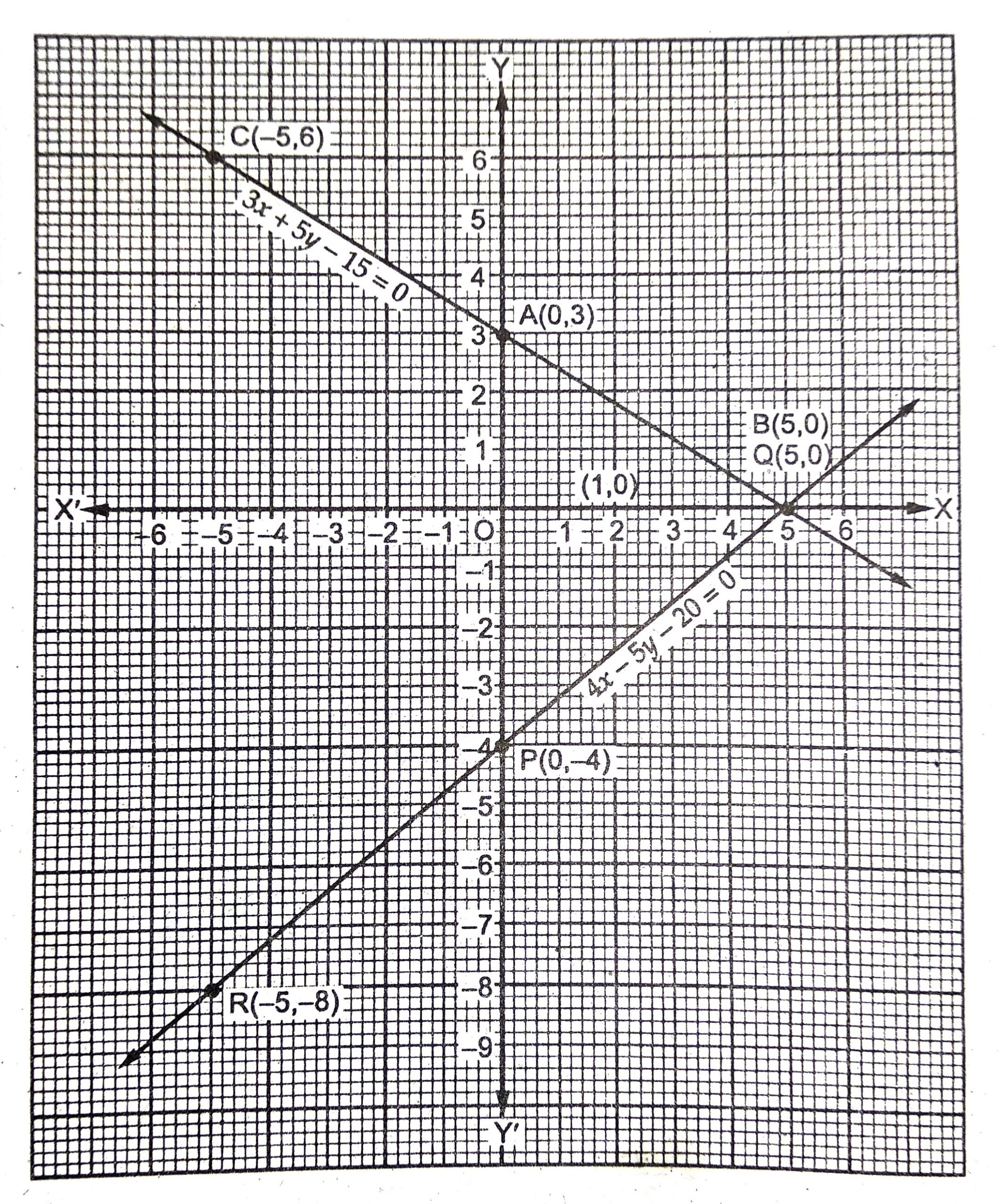
चूँकि समीकरण 4x – 5y – 20 = 0 का आलेख QPR तथा समीकरण 3x + 5y – 15 = 0 आलेख CAQ एक दूसरे को Q ( 5, 0) पर प्रतिच्छेद करते हैं।
अतः x = 5, y = 0 दिये गए समीकरण युग्म का हल होगा।
इन दानों रेखाओं एवं y- अक्ष के बीच बना त्रिभुज QPA है ।
∴ΔQPA के शीर्ष बिन्दु क्रमशः (5, 0), P(0, – 4) एवं A (0, 3) है।
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here