Bihar Board Class 9Th Mathematics chapter 4 दो चरों वाले रैखिक समीकरण Solutions | Bseb class 9Th Chapter 4 दो चरों वाले रैखिक समीकरण Notes
Bihar Board Class 9Th Mathematics chapter 4 दो चरों वाले रैखिक समीकरण Solutions | Bseb class 9Th Chapter 4 दो चरों वाले रैखिक समीकरण Notes
प्रश्न- एक नोटबुक की कीमत एक कलम की कीमत से दो गुनी है। इस कथन को निरूपित करने के लिए दो चरों वाला एक रैखिक समीकरण लिखिए।
संकेत : मान लीजिए, नोट बुक की कीमत x रु० है और कलम की कीमत y रु० हैं।
उत्तर—हल : माना कि पुस्तक का मूल्य = x
कलम का मूल्य = y
चूँकि एक पुस्तक का मूल्य, एक कलम के मुल्य से दोगुनी है। अतः अभीष्ट दो चरों वाले रैखिक समीकरण = x = 2y
प्रश्न- निम्नलिखित रैखिक समीकरणों को ac + by + c = 0 के रूप में व्यक्त कीजिए और प्रत्येक स्थिति में a, b और c के मान बताइए :
(i) 2x + 3y = 9.35 (ii) x – y/5 – 10 = 0
(iii) – 2x + 3y = 6 (iv) x = 3y
उत्तर— हल : (i) 2x + 3y = 9 को 2x + 3y – 9 = 0 के रूप में लिखा जा सकता है।
इसकी ax + by + c = 0 से तुलना करने पर
a = 2, b = 3 और c = – 9
(ii) x – y/5 – 10 = 0 को तुलना ax + by + c = 0 से करने पर
a = 1, b = -1 और c = – 10
(iii) a = −2, b = 3 और c = – 6
(iv) a = 1, b = −3 और c = 0
प्रश्न- बताइए कि निम्नलिखित हलों में कौन-कौन समीकरण x – 2y = 4 के हल हैं और कौन-कौन हल नहीं हैं :
(i) (0, 2) (ii) (2,0) (iii) (4, 0)
उत्तर— हल : (i) x = 0 तथा y = 2, x – 2y = 4 के बाएँ पक्ष में रखने पर
बायाँ पक्ष = 0 – 2 x 2 = 4 दायाँ पक्ष
∴ x = 0, y = 2 इसका हल नहीं है।
(ii) x – 2y = 4 के बाएँ पक्ष में x = 2, y = 0 रखने पर
बायाँ पक्ष = 2 – 2 x 0 = 2 – 0 = 2 ≠ दायाँ पक्ष
∴ x = 2, y = 0 इसका हल नहीं है।
(iii) x – 2y = 4 के बाएँ पक्ष में x = 4, y = 0 रखने पर
बायाँ पक्ष = 4 – 0 = 4 = दायाँ पक्ष
∴ x = 4, y = 0 इसका हल है।
प्रश्न- k का मान ज्ञात कीजिए जबकि x = 2, y = 1 समीकरण 2x + 3y = k का एक हल हो।
उत्तर— हल : यदि x = 2, y = 1 समीकरण 2x + 3y = k का हल है तो ये मान समीकरण को सन्तुष्ट करेंगे ।
∴ 2 x 2 + 3 x 1 = k = k = 4 + 3 = 7
प्रश्न- दो चरों वाले निम्नलिखित रैखिक समीकरणों में से प्रत्येक का आलेख खींचिए:
(1) x + y = 4 (ii) x – y = 2 (iii) y = 3x (iv) 3 = 2x + y
Note : आलेख खिंचने के लिए हम समीकरण में x या y का उचित मान रखकर एक Table बनाते है । फिर सभी निर्देशांक को सीधी रेखासे मिला देते हैं ।
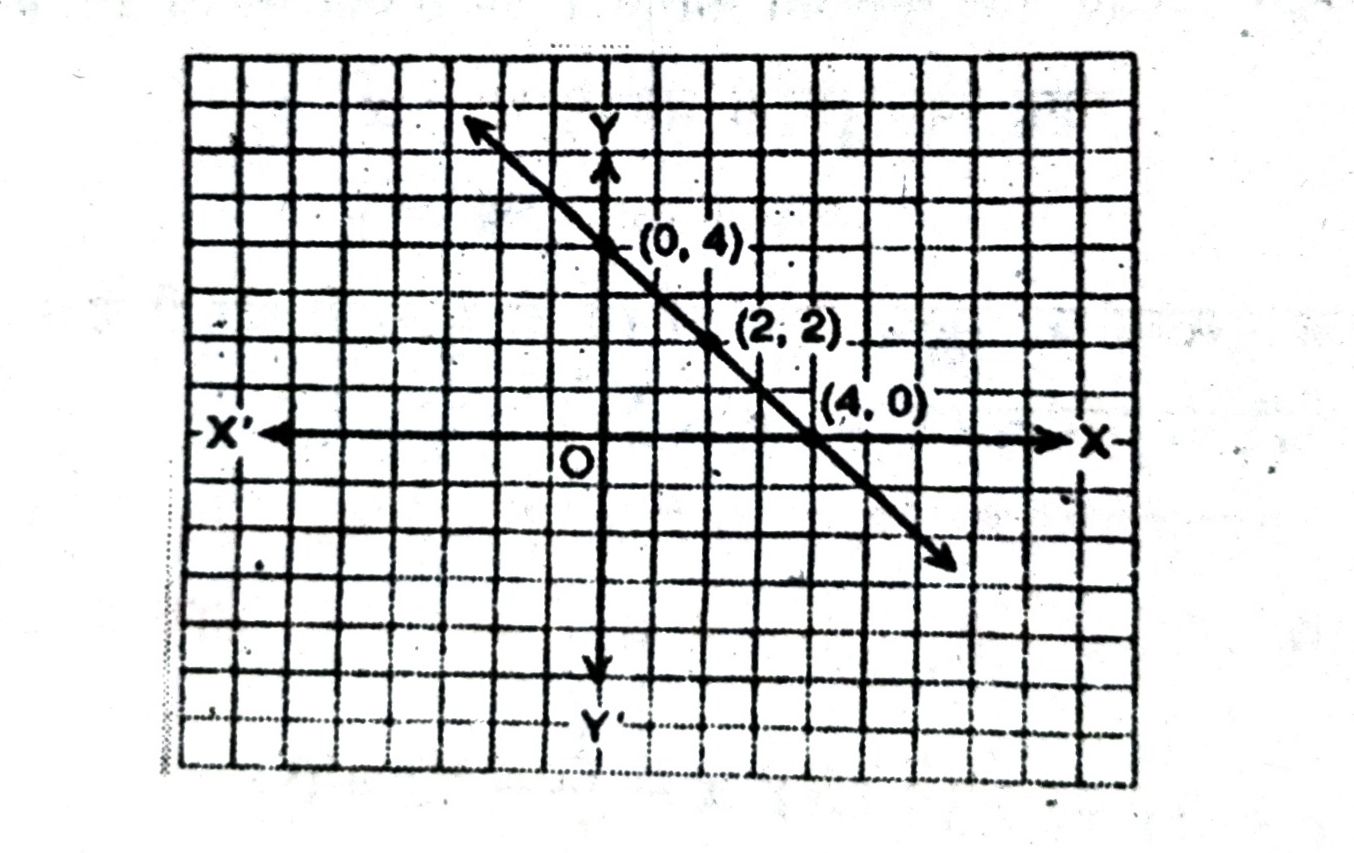
उत्तर— हल : (i) जब x + y = 4 ⇒ y = 4 x जब x = 0, y = 4 – 0 = 4
जब x = 2, y = 4 – 2 = 2 जब x = 4, y = 4-4 = 0
अतः हमारे पास निम्नलिखित सारणी हैं :
| x | 0 | 2 | 4 |
| y | 4 | 2 | 0 |
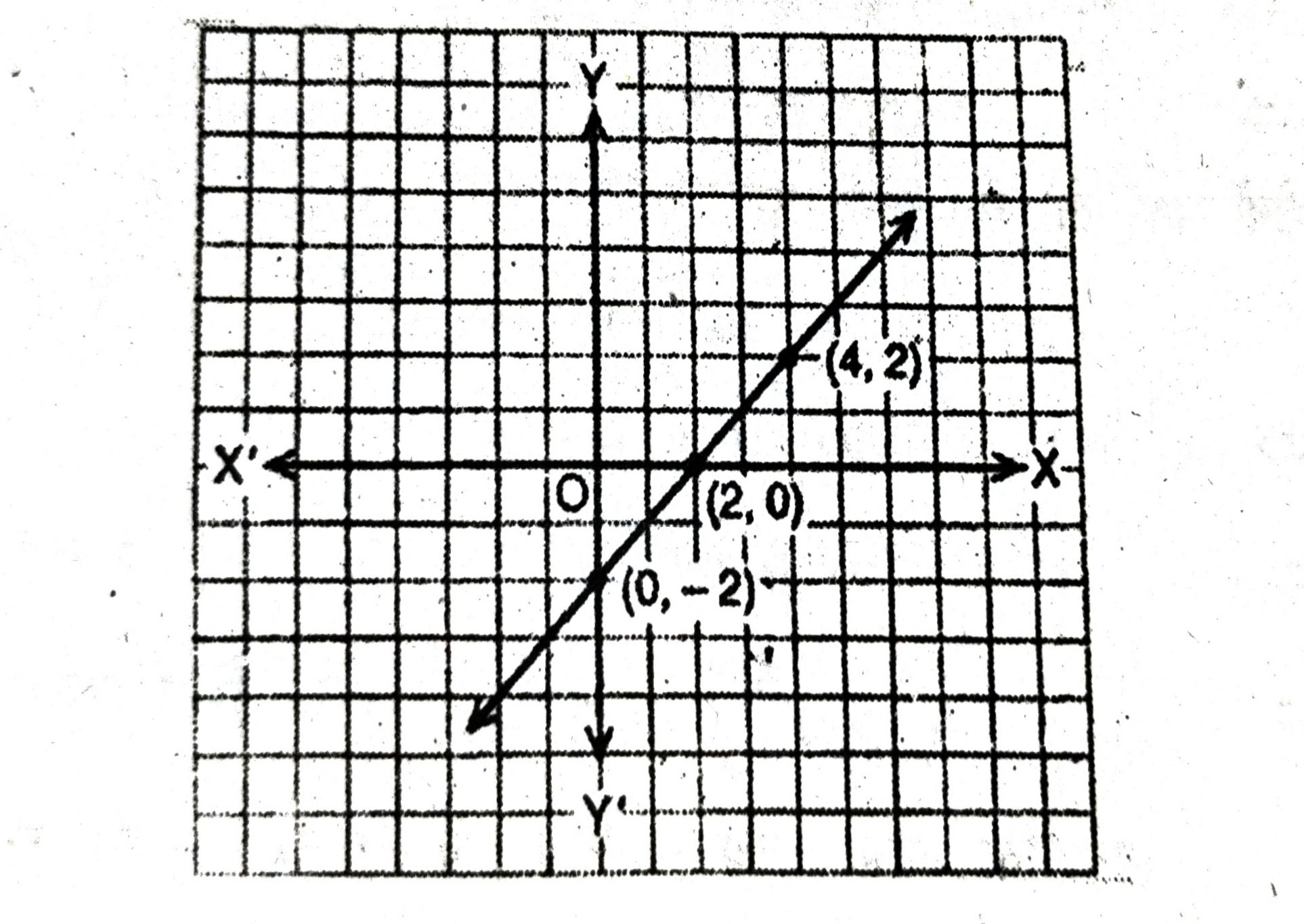
(ii) जब x – y = 2 ⇒ y = x – 2 जब x = 0, y = 0 – 2 = -2
जब x = 2, y = 2 – 2 = 0 जब x = 4, y = 4 – 2 = 2
अतः हमारे पास निम्नलिखित सारणी हैं :
| x | 0 | 2 | 4 |
| y | -2 | 0 | 2 |
प्रश्न- (i) एक घर वाले (ii) दो घर वाले
समीकरण के रूप में y = 3 का ज्यामितीय निरूपण कीजिए ।
उत्तर— हल : (i) y = 3 को एक चर का रैखिक समीकरण लेते हुए अंक रेखा पर इसका हल निम्नलिखित तरीके से दर्शाया गया है । y = 3

(ii) हम जानते हैं कि y = 3 को 0.x + y = 3 के रूप में लिखा जा सकता । अब x के सभी मान सम्भव हैं चूँकि 0.x = 0 लेकिन y के द्वारा इस सम्बन्ध को जरूर सन्तुष्ट करना चाहिए ।
अतः समीकरण के लिए तीन हल हैं ।
x = 0, y = 3, x = -2, y= 3

हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here