Bihar Board Class 9Th Mathematics chapter 6 रेखाएँ और कोण Solutions | Bseb class 9Th Chapter 6 रेखाएँ और कोण Notes
Bihar Board Class 9Th Mathematics chapter 6 रेखाएँ और कोण Solutions | Bseb class 9Th Chapter 6 रेखाएँ और कोण Notes
प्रश्न- आकृति में रेखाएँ AB और CD बिंदु 0 पर प्रतिच्छेद करती हैं। यदि ∠AOC + ∠BOE = 70° है और ∠BOD = 40° है, तो ∠BOE और प्रतिवर्ती ∠COE ज्ञात कीजिए ।
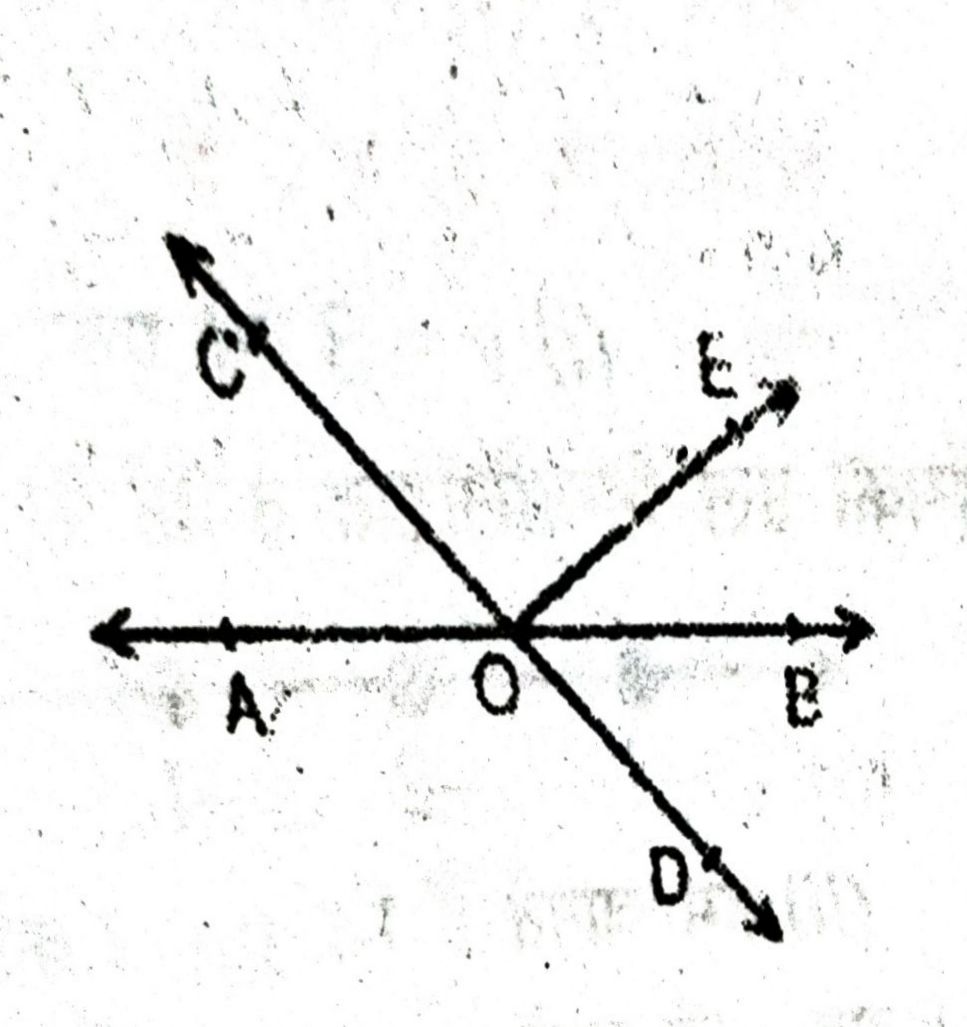
उत्तर— हल : चूंकि OA तथा OB विपरीत किरणें हैं। इसलिए AB एक रेखा है। चूंकि किरण OC, AB पर आधारित है। इसलिए,
∠AOC + ∠COB = 180° [ रैखिक युग्म]
⇒ ∠AOC + ∠COE + ∠BOE = 180°
[∴ ∠COB = ∠COE + ∠BOE]
⇒ (∠AOC + ∠BOE) + ∠COE = 180°
[∴ ∠AOC +∠BOE = 70° (दिया है ।)
COE = 180° – 700 = 1100
∴ प्रतिवर्ती ∠COE = 3600 – 1100 = 2500
चूंकि OC तथा OD विपरीत किरणें हैं इसलिए
∠COE + ∠EOD = 180°. [रैखिक युग्म]
⇒ ∠COE + ∠BOE +∠ BOD = 180°
⇒ 110° + ∠BOE + 40° = 180°
⇒ [∴ ∠COE = 110° (ऊपर सिद्ध किया गया है), ∠BOD = 40° (दिया है)]
∠BOE = 180° – 110° – 40° = 30°
अतः ∠BOE = 30° तथा प्रतिवर्ती ∠COE = 250°
प्रश्न- आकृति में, रेखाएं XY और MN बिंदु O पर प्रतिच्छेद करती हैं। यदि ∠POY = 90° और a : b = 2 : 3 है, तो ज्ञात कीजिए।
उत्तर— हल चूंकि a: b = 2:3 तथा a + b = ∠POX = ∠POY = 90° तथा अनुपातों का योग 2 + 3 = 5
⇒ (x + y) + (w + z) = 360°
∴ a = 2/5 × 90° = 2 x 18° = 36°
तथा ba = 3/5 x 90° = 3 x 18° = 54 °
MOX + ∠XON = 180° [ रैखिक युग्म]
⇒ c + b = 180°⇒ c + 54° = 180°⇒ c = 180° – 54° = 126⁰
अत: c = 126⁰
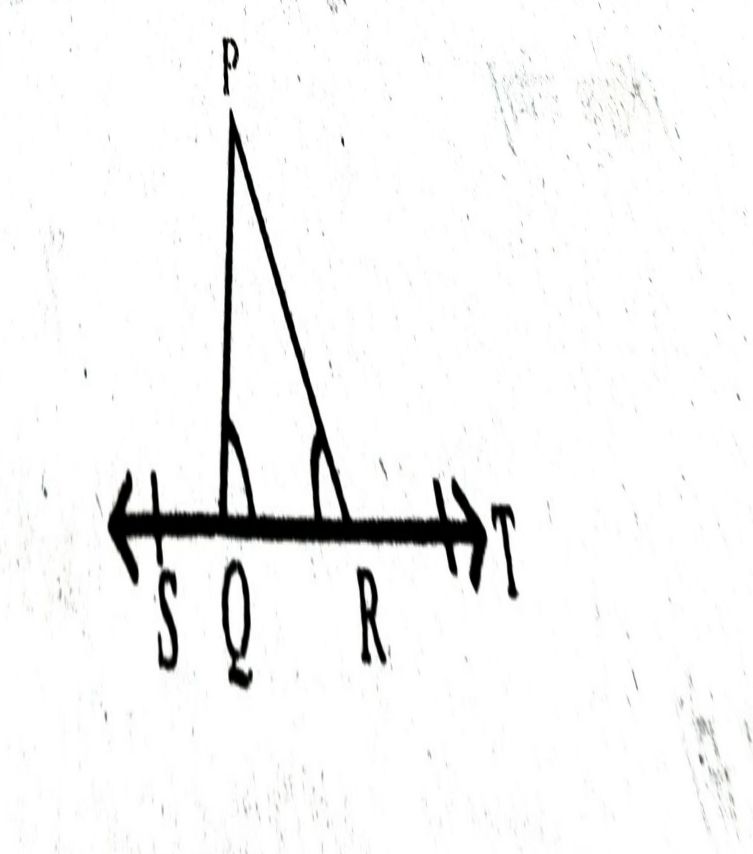
प्रश्न- आकृति में यदि PQR = PRQ है, तो सिद्ध कीजिए कि PQS = PRT है ।
उत्तर— हल :
∴ ∠PQS +∠PQR = 180° [रैखिक युग्म] … (1)
∴ ∠PRQ + ∠PRT = 180° [रैखिक युग्म] …(2)
समी० (1) तथा (2) से
∠PQS + ∠PQR = ∠PRQ + ∠PTR …(3)
∴ ∠POR = ∠PRQ [दिया है] …. (4)
समी० (4) को (3) में से घटाने पर ∠PQS = ∠PRT.
प्रश्न- आकृति में, x और y के मान ज्ञात कीजिए और फिर दर्शाइए कि AB || CD है।
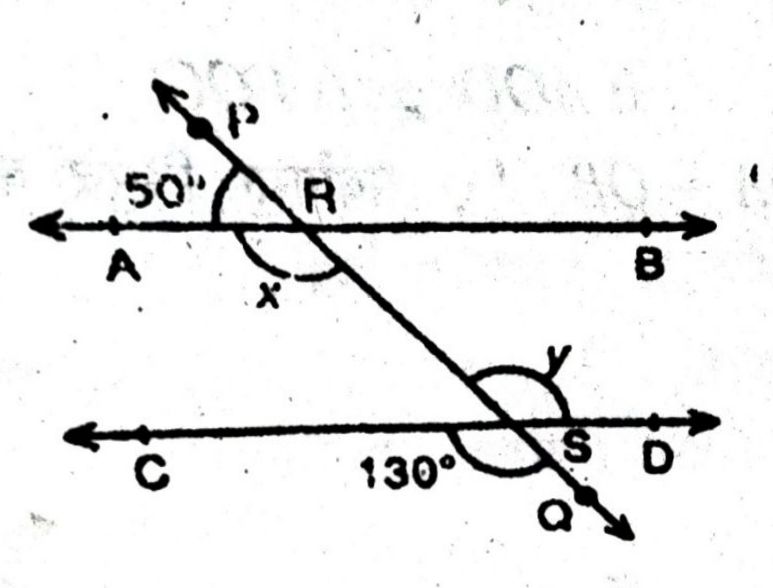
उत्तर— हल : चूँकि AB || CD तथा तिर्यक रेखा PQ उनको क्रमश: R तथा S पर काटती है।
∴ ∠ARS = ∠RSD. [एकान्तर कोण]
x = y
और ∠RSD = ∠CSQ. [शीर्षाभिमुख कोण]
⇒ y = 130° [CSQ = 130°]
अत : x = y = 130°
प्रश्न- आकृति में, यदि PQ || ST, ∠PQR = 110° और ∠RST – 130° है, तो ∠QRS ज्ञात कीजिए।
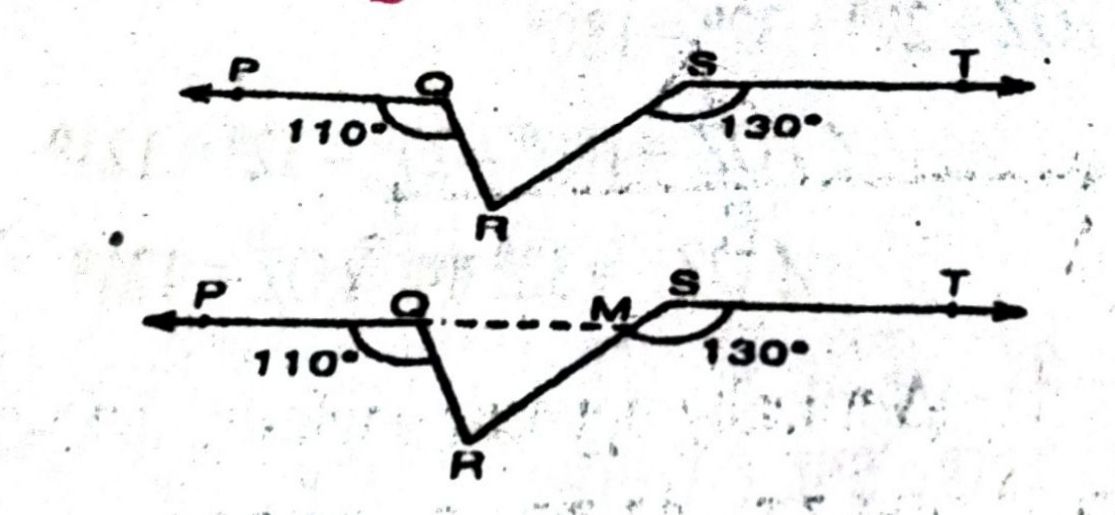
उत्तर— हल : PQ को M बिन्दु पर काटने के लिए SR तक बढ़ाया । अब PM || ST तथा तिर्यक रेखा SM क्रमशः उनको M तथा R पर काटती है।
∴ ∠SMQ =∠TSM [एकातर कोण]
∠SMQ = 130°
∠QMR = 180° – 130° = 50° [∴ ∠SMQ + ∠QMR = 180°
∠PQR + ∠ROM = 180°
110° + ∠ROM = 180° ⇒ ∠ROM = 20°
∠QRS = 180° – (70° + 50°) = 60°
[∴ एक त्रिभुज के तीनों कोणों का योग 180° होता है]
प्रश्न- आकृति में ΔPOR की भुजाओं QP और RQ को क्रमशः बिंदुओं S तथा T तक बढ़ाया गया है। यदि ∠SPR = 135° है और ∠PQT = 110° है, तो ∠PRO ज्ञात कीजिए :
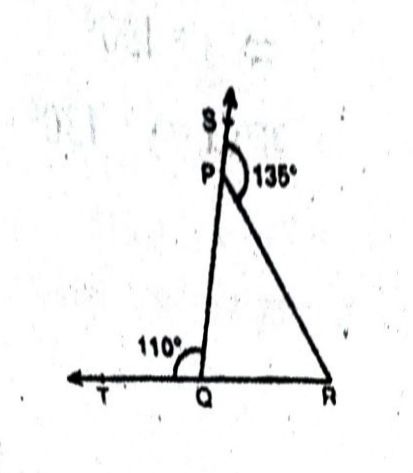
उत्तर— हल : ∠QPR + ∠SPR = 180° [रैखिक कोण]
∠QPR + ∠135° = ∠180°
∠QPR + ∠180° – 135° = 45°
अब TQP = ∠QPR + ∠PRQ [बाह्य कोण प्रमेय से]
110° = 45° + ∠PRQ
∠PRQ = 110° – 45° = 65°
अतः ∠PRQ = 65°
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here