Bihar Board Class 9Th Mathematics chapter 8 चतुर्भुज Solutions | Bseb class 9Th Chapter 8 चतुर्भुज Notes
Bihar Board Class 9Th Mathematics chapter 8 चतुर्भुज Solutions | Bseb class 9Th Chapter 8 चतुर्भुज Notes
प्रश्न- एक चतुर्भुज के कोण 3 : 5 : 9 : 13 के अनुपात में हैं। इस चतुर्भुज के सभी कोण ज्ञात कीजिए।
उत्तर— हल : माना कोण हैं ( 3x)°, (5x)°, (9x)° और (13x)°
तब 3x + 5x + 9x + 13x = 360
⇒ 30x = 369 = x ⇒ 360/30 = 12
∴ कोण हैं (3 × 12)°, (5 × 12)°, (9 × 12)° और (13 × 12)° अर्थात 36°, 60°, 108° और 156° हैं।
प्रश्न- ABCD एक आयत है जिसमें विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है। दर्शाइए कि (i) ĀBCD एक वर्ग है (ii) विकर्ण BD दोनों कोणों B और D को समद्विभाजित करता है।
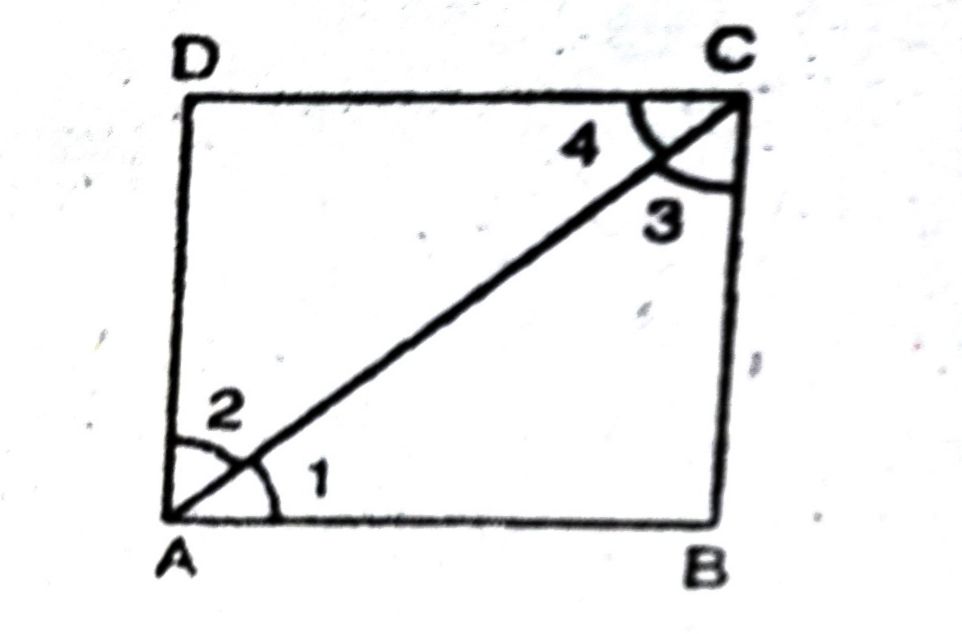
उत्तर— हल : दिया है: ABCD एक आयत है जिसमें विकर्ण AC कोण A और कोण C को समद्विभाजित करता है।
सिद्ध करना है: (i) ABCD एक वर्ग है ।
(ii) विकर्ण BD कोण B और कोण D को समद्विभाजित करता है ।
प्रमाण : (i) चूंकि आयत ABCD में AC कोण A और कोण C को समद्विभाजित करता है।
∴ ∠1 = ∠2 = ∠3 = ∠4 [∴ प्रत्येक = 90° / 2 = 45°]
∴ ADC में, ∠2 = ∠4
⇒ AD = CD [सम्मान कोणों की सम्मुख भुजाएं]
इस प्रकार, आयत ABCD एक वर्ग है |
(ii) वर्ग में विकर्ण कोणों को समद्विभावित करता है | अंत: BD कोण B और कोण D को समद्विभाजित करता है l
प्रश्न- ABCD एक समलंब है, जिसमें AB || DC है। साथ ही, BD एक विकर्ण है और E भुजा AD का मध्य बिंदु है। Eसे होकर एक रेखा AB के समांतर खींची गई है, जो BC को F पर प्रतिच्छेद करती है ( देखिए आकृति) । दर्शाइए कि F भुजा BC का मध्य बिंदु है ।

उत्तर— हल: दिया है : समलंब चतुर्भुज ABCD में AB || DC
E भुजा AD का मध्य बिंदु है, EF || AB.
सिद्ध करना है: F,BC का मध्य बिंदु है।
रचना : ΔDAB को मिलाया । यह EF को G पर काटती है प्रमाण : DAB में, E भुजा AD का मध्य बिंदु है। [दिया है]
EG || AB [∴ EF ΙΙ AB]
∴ विलोम मध्य बिंदु प्रमेय द्वारा G भुजा DB का मध्य बिंदु है ।
BCD में G भुजा BD का मध्य बिंदु है । [सिद्ध है]
GF || DC [∴ AB || DC, EF || AB ⇒ DC ll EF]
∴ विलोम मध्य-बिंदु प्रमेय द्वारा F भुजा BC का मध्य बिंदु है l
प्रश्न- दशाइए कि किसी चतुर्भुज की सम्मुख भुजाओं के मध्य बिंदुओं को मिलाने वाले रेखाखंड परस्पर समद्विभाजित करते हैं।
उत्तर— हल दिया है: चतुर्भुज ABCD में, P, Q, R और S क्रमश: AB, BC, CD और DA के मध्य-बिंदु हैं | PR और QS एक-दूसरे को O पर प्रतिच्छेदित करते हैं।
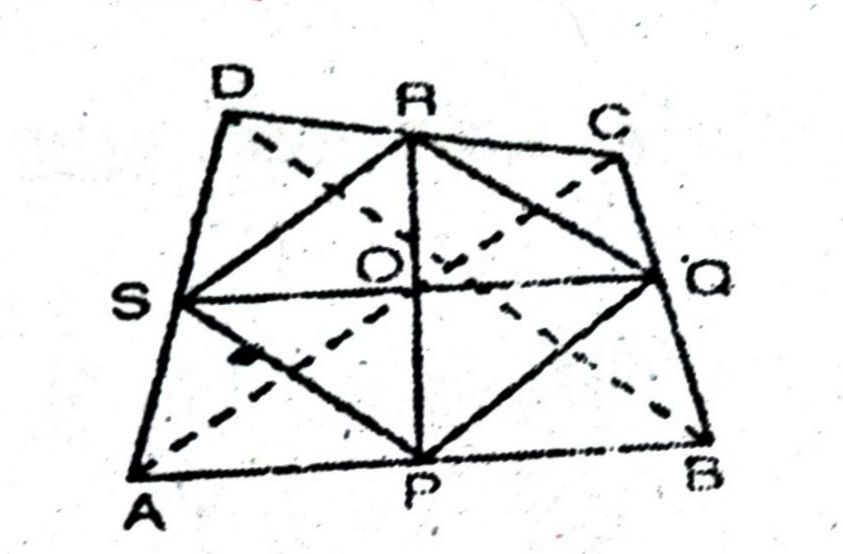
सिद्ध करना है : OP = OR, OQ = OS.
रचना : PQ, QR, RS, SP, AC और BD को मिलाया।
प्रमाण: ABC में, P और Q क्रमश: AB और BC के मध्य बिंदु हैं l
∴ PQ || AC और PQ = 1/2 AC
इसी प्रकार हम सिद्ध कर सकते हैं कि
RS || AC और RS = ½ AC
∴ PQ || SR और_PQ = SR
इस प्रकार, चतुर्भुज PQRS की सम्मुख भुजाओं का एक युग्म समानांतर और समान है।
∴ चतुर्भुज PORS एक समांतर चतुर्भुज है ।
∴ चूंकि समांतर चतुर्भुज के विकर्ण एक – दूसरे को समद्विभाजित करते हैं।
∴ समांतर चतुर्भुज PQRS के विकर्ण PR और QS अर्थात् चतुर्भुज ABCD की सम्मुख भुजाओं के मध्य बिंदुओं से मिलने वाले रेखाखंड एक-दूसरे को समद्विभाजित करते हैं।
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here