Bihar Secondary School Sample Paper Solved | BSEB Class 10th Sample Sets with Answers | Bihar Board class 10th Sample Paper Solved | Bihar Board Class 10th mathematics Sample set – 2
Bihar Secondary School Sample Paper Solved | BSEB Class 10th Sample Sets with Answers | Bihar Board class 10th Sample Paper Solved | Bihar Board Class 10th mathematics Sample set – 2
1. π का दशमलव प्रसार होगा
(A) अपरिमेय
(B) असांत आवर्ती
(C) असांत अनावर्ती
(D) (A) एवं (B) दोनों
2. √23 किस प्रकार की संख्या है ?
(A) परिमेय
(B) अपरिमेय
(C) सम
(D) विषम
3. सबसे छोटी अभाज्य संख्या कौन-सी है ?
(A) 2
(B) 3
(C) 5
(D) 7
4. यदि द्विघात बहुपद (k – 1)x2 + kx + 1 का एक शून्यक – 3 हो तो k का मान होगा
(A) 4/3
(B) – 4/3
(C) 2/3
(D) -2/3
5. द्विघात बहुपद ax2 + bx + c का आलेख किस प्रकार का होता है?
(A) वृत्ताकार
(B) त्रिभुजाकार
(C) परवलयाकार
(D) एक सरल रेखा
6. बहुपद 4x2– 3 के शून्यक होंगे
(A) √3/5 , -√3/5
(B) 1/2, -1/2
(C) √3/2, – √3/2
(D) 3/4, -3/4
7. जिस समीकरण युग्म के आलेख एक-दूसरे के सामान्तर हों, उसे कहते हैं
(A) विरोधी
(B) अविरोधी
(C) आश्रित
(D) इनमें से कोई नहीं
8. रैखिक समीकरण युग्म x + 2y = 5 तथा 3x + 12y = 10 का हल होगा
(A) एकल
(B) कोई हल नहीं
(C) एक से अधिक
(D) अनन्त
9. द्विघात-समीकरण 3x2 – 2x + 1/3 = 0 के विवेचक का मान होगा
(A) 0
(B) 1/2
(C) 1
(D) √3
10. यदि द्विघात समीकरण x2 – 7x + p = 12 के मूलों का गुणनफल – 6 हो तो P का मान होगा
(A) 6
(B) –6
(C) 8
(D) 10
11. यदि A.P. का 5 है तो T18 – T13 का मान होगा
(A) 15
(B) 20
(C) 25
(D) 30
12. यदि किसी A.P. का प्रथम पद ‘a’ और सार्वअन्तर ‘d’ हो तो इसका nवाँ पद कौन सा होगा ?
(A) a + (n – 2)d
(B) a + (n – 1)d
(C) a + nd
(D) a – (n – 1)d
13. यदि दो समरूप त्रिभुजों की भुजाएँ 4 : 9 के अनुपात में हों तो इनके क्षेत्रफलों का अनुपात होगा
(A) 2 : 3
(B) 4 : 9
(C) 16 : 81
(D) 81 : 16
14. यदि किसी चतुर्भुज के विकर्ण एक-दूसरे को समान अनुपात में विभाजित करते हैं तो वह चतुर्भुज होगा
(A) सामांतर चतुर्भुज
(B) समलम्ब चतुर्भुज
(C) वर्ग
(D) आयत
15. दी गई आकृति में ΔABC का परिमाप होगा
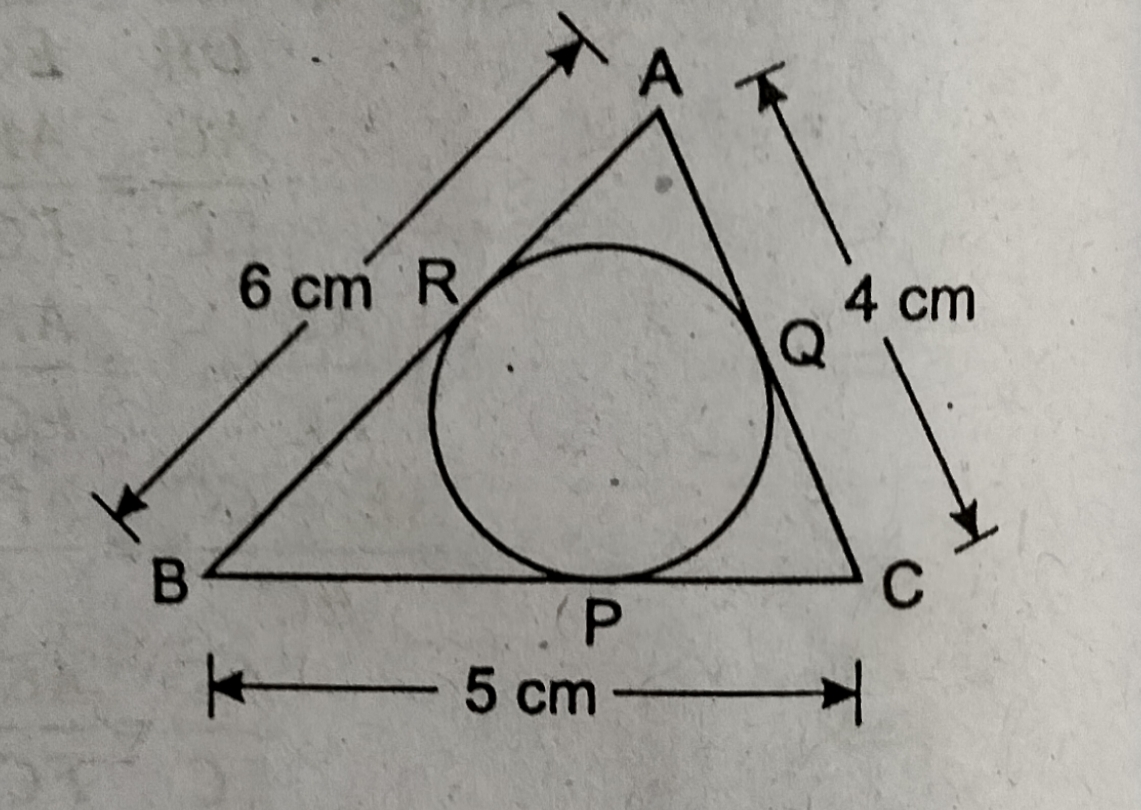
(A) 30cm
(B) 60cm
(C) 45cm
(D) 15cm
16. tan 15°. tan 20°, tan 70°, tan 75° का मान होगा
(A) 1
(B) 2
(C) 0
(D) -1
17. यदि √3 tanθ = 3sin , तब sin2θ – cos2θ का मान होगा
(A) √3
(B) 2/3
(C) 1/3
(D) 1/√3
18. यदि tan(α + β) = √3 एवं tanα = 1/√3 हो तो tanβ का मान होगा
(A) 1/6
(B) 1/7
(C) 1/√3
(D) 7/6
19. 2tan 30° / 1 + tan2 30° का मान हैं
(A) sin 60°
(B) cos 60°
(C) tan 60°
(D) sec 60°
20. यदि secθ = 13/12 हो तो cotθ का मान होगा
(A) 5/12
(B) 5/13
(C) 12/5
(D) 13/5
21. यदि किसी घनाभ की लम्बाई I, चौड़ाई b तथा ऊँचाई h हो तो, घनाभ का विकर्ण होगा
(A) Ibh
(B) √l2 + b2+ h2
(C) 2(lb + bh +lh
(D) 2h(l + b)
22. यदि किसी गोले की त्रिज्या 3 गुनी हो जाती है, तो इसका आयतन होगा
(A) 3 गुना
(B) 6 गुना
(C) 9 गुना
(D) 27 गुना
23. एक पहिए का व्यास 40cm है। 176m की दूरी तय करने में इसे कितना चक्कर लगाना पड़ेगा?
(A) 140
(B) 150
(C) 160
(D) 166
24. दी गई आकृति में TP तथा TQ दो स्पर्श रेखाएँ हैं। ∠POQ +∠PTQ बराबर होगा
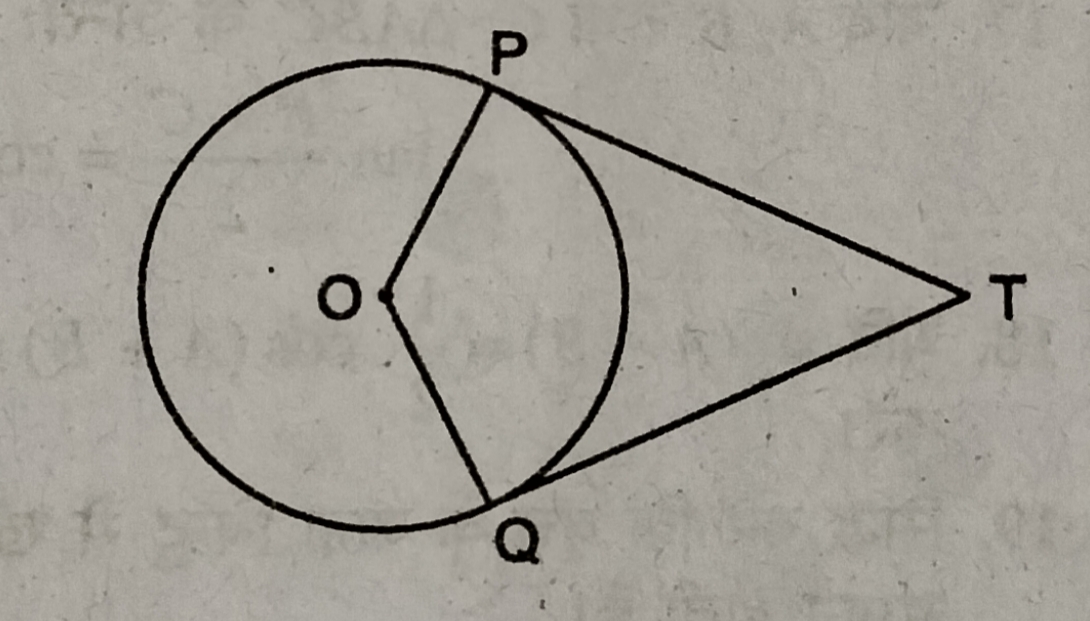
(A) 90°
(B) 120°
(C) 150°
(D) 180°
25. यदि एक वृत्त का परिमाप और क्षेत्रफल संख्यात्मक रूप में समान है, तो वृत्त की त्रिज्या होगी
(A) 2 मात्रक
(B) 4 मात्रक
(C) π मात्रक
(D) 6 मात्रक
26. निम्नलिखित में किसका निर्धारण आलेख द्वारा नहीं किया जा सकता है ?
(A) माध्य
(B) माध्यिका
(C) बहुलक
(D) इनमें से कोई नहीं
27. निम्नलिखित में से कौन केन्द्रीय प्रवृति की माप नहीं है।
(A) माध्य
(B) माध्यिका
(C) बहुलक
(D) इनमें से कोई नहीं
28. किसी प्रयोग में सभी प्रारंभिक घटनाओं की प्रायिकताओं का योग होता है
(A) 2
(B) 0.5
(C) 1
(D) 2.5
29. यदि P(E) = 0.07 हो तो P (E’) बराबर होगा
(A) 0.93
(B) 0.09
(C) 0.07
(D) कोई नहीं
30. सूर्य का उन्नयन कोण 60° है, तो उस मीनार की ऊँचाई क्या होगी जिसकी छाया 30 मी दूर बनता हो ?
(A) 15 मी
(B) 18 मी
(C) 30√3 मी
(D) 15√2 मी
31. √2, √8, √18, √32 में पदान्तर क्या है?
(A) √2
(B) √3
(C) 2
(D) इनमें से कोई नहीं
32. यदि बिन्दुएँ (a, 0), (0, b) और (1, 1) संरेख है तब a + b =
(A) –ab
(B) ab
(C) 1/ab
(D) -1/ab
33. बिन्दुओं (2, 3) और (4, 1) के बीच की दूरी होगी
(A) 2
(B) 2√2
(C) 4
(D) 8
34. यदि तीन बिन्दु संरेख हों तो, उनसे बने त्रिभुज का क्षेत्रफल होगा
(A) 0
(B) 1
(C) 2
(D) इनमें से कोई नहीं
35. ताश के पत्तों की एक गड्डी को अच्छी तरह फेंटा गया है। एक पत्ती यादृच्छया निकाली जाती है, तो इसके इक्का होने की प्रायिकता है
(A) 1/4
(B) 1/36
(C) 1/13
(D) 4/13
36. 5, 15 और 20 के ल०स० और म०स० का अनुपात है
(A) 9 : 1
(B) 4 : 3
(C) 11 : 1
(D) 12 : 1
37. दो संख्याओं P एवं 18 का ल०स० 36 तथा म०स० 2 है तो P का मान है
(A) 2
(B) 3
(C) 4
(D) 1
38. 96 का अभाज्य गुणनखंड क्या होगा ?
(A) 24 x 34
(B) 23 x 33
(C) 25 x 3
(D) 2 x 35
39. यदि m एक धनात्मक पूर्णांक है तो धनात्मक विषम पूर्णांक का रूप होगा
(A) 4m + 2
(B) 4m + 4
(C) 4m + 1
(D) इनमें से कोई नहीं
40. √1 + tan2A बराबर क्या होगा, जबकि (0°≤ A ≤ 90° ) है
(A) cot A
(B) sec A
(C) cos A
(D) sin A
41. यदि 3α = 90° हो तो sin α का मान होगा
(A) 1 / √3
(B) √3 / 4
(C) 1 / 2
(D) √3 / 2
42. (secθ + tanθ) (1 – sin θ)=?
(A) sin θ
(B) cosec θ
(C) cos θ
(D) sec θ
43. यदि द्विघात समीकरण 2x2 – px + p = 0 का मूल समान हो तो ‘p’ का मान होगा
(A) 4
(B) केवल 0
(C) 0, 8
(D) केवल 8
44. 3, 5, 4, 3, 2, 3, 1, 3 का बहुलक है
(A) 1
(B) 5
(C) 4
(D) 3
45. यदि किसी सामान्तर श्रेणी का छठा एवं बारहवाँ पद 13 और 25 है, तो इसका पहला पद है
(A) 4
(B) 3
(C) 2
(D) 5
46. यदि (x + 2), 3x और (4x + 1) सामान्तर श्रेणी में हो तो ‘x’ का मान होगा
(A) 1
(B) 2
(C) 3
(D) 4
47. यदि α, β बहुपद x2 – 3x + 5 के शून्यक हों तो (α + β) का मान होगा
(A) 3,
(B) 5,
(C) -3
(D) – 5
48. यदि x2 + px – q के शून्यक एक दूसरे के व्युत्क्रम हों तो ‘q’ का मान होगा
(A) -1
(B) 1
(C) p
(D) p2
49. यदि a1 / a2 = b1 / b2 = c1 / c2 तो समीकरण निकाय a1x + b1 y + c1 = 0 and a2x + b2y + c2 = 0 का हल होगा
(A) अद्वितीय हल
(B) कोई हल नहीं
(C) अनन्त हल
(D) इनमें से कोई नहीं
50. रैखिक समीकरण में चर के घात की संख्या होती है
(A) 1
(B) 2
(C) 3
(D) इनमें से कोई नहीं
51. दो घनों के आयतनों का अनुपात 1 : 27 है, तो उनके पृष्ठीय क्षेत्रफलों का अनुपात होगा
(A) 1 : 3
(B) 1 : 8
(C) 1 : 9
(D) 1 : 18
52. किसी वृत्ताकार क्षेत्र की परिधि 4π मीटर है तो उसकी त्रिजया होगी’
(A) 1 मीटर
(B) 2 मीटर
(C) π मीटर
(D) इनमें से कोई नहीं
53. ठीक 4 : 24 अपराह्न पर घंटे की सुई दोपहर के बाद कितने डिग्री घूम जा चुकी होगी
(A) 135°
(B) 134°
(C) 133°
(D) 132°
54. चित्र में BC II DE, AD : AB=AE : x तो x बराबर है
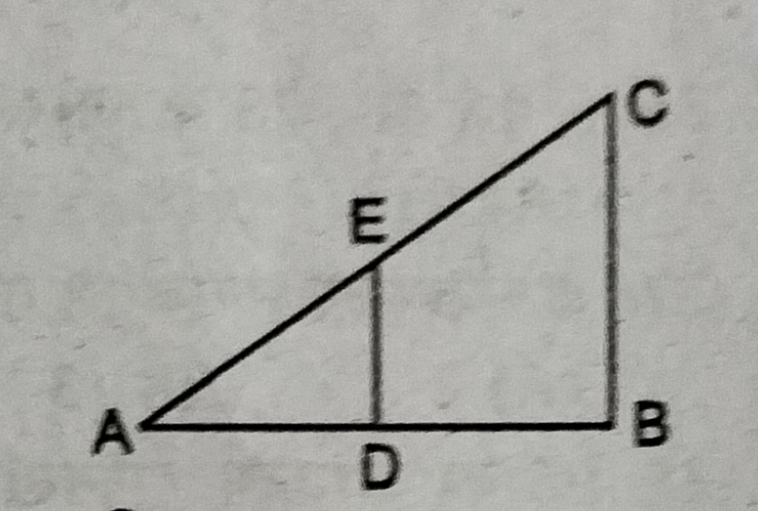
(A) BD
(B) BC
(C) AC
(D) EC
55. दी गई आकृति में AD का मान ‘b’ तथा ‘ c ‘के पदों में क्या होगा
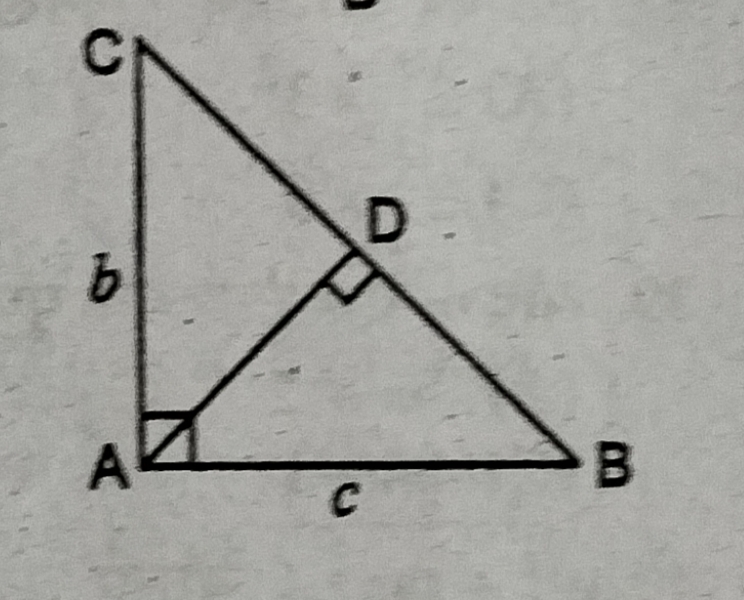
(A) bc / √b2 + c2
(B) √bc
(C) b2c2 / b2 + c2
(D) √b2 + c2 / bc
56. यदि θ = 60° हो तो sin θ + cos θ का मान होगा
(A) 1/√2
(B) √3 – 1 / 2
(C) √3 + 1
(D) 1
57. sin π/4 – cos π/4 का मान है
(A) 2
(B) 0
(C) –1
(D) 1
58. y-अक्ष पर स्थित किसी बिन्दु का x नियामक क्या होगा ?
(A) शून्य
(B) y
(C) x
(D) इनमें से कोई नहीं
59. दो बिन्दु P(3, – 3) और Q(-3, – 3) को मिलाने वाली रेखाखण्ड के मध्यबिन्दु का नियामक क्या होगा ?
(A) (1, 0)
(B) (0, 3)
(C) (0, 0)
(D) (0, 2)
60. उस बिन्दु का नियामक जो बिन्दु (1,1) तथा (2, 3) को जोड़ने वाली रेखाखण्ड को 2:3 के अनुपात में विभाजित करती है
(A) 7/5 , 9/5
(B) 7, 9
(C) 7/3, 3
(D) इनमें से कोई नहीं
प्रश्न- दो खिलाड़ी संगीता एवं रेशमा टेनिस का एक मैच खेलते हैं, यह ज्ञात है कि संगीता द्वारा मैच जीतने की प्रायिकता 0.62 है। रेशमा के मैच जीतने की प्रायिकता क्या है ?
उत्तर– माना कि संगीता द्वारा मैच जीतने की प्रायिकता P(E) है तथा रेशमा द्वारा मैच जीतने की प्रायिकता P(E’) है।
∴ P(E) + P(E’) =1
⇒ 0.62 + P(E’) =1
∴ P(E’) = 1 – 0.62 = 0.38
अतः रेशमा द्वारा मैच जीतने की प्रायिकता = 0.38; Ans.
प्रश्न- एक पेटी में 12 गेंदें हैं जिनमें x गेंदें काली हैं। यदि इसमें से एक गेंद यादृच्छया निकाली जाती है तो इसकी प्रायिकता ज्ञात करें कि वह गेंद काली है।
उत्तर– पेटी में गेंदों की संख्या = 12
∴ सभी संभव परिणामों की संख्या =12
इन 12 गेंदों में काली गेंदों की संख्या = x
∴ काली गेंद की प्रायिकता= काली गेंद की संख्या / कुल गेंद की संख्या = x/12; Ans.
प्रश्न- किसी गेंदबाज द्वारा 10 क्रिकेट मैचों के लिए विकेटों की संख्या 2, 6, 4, 5, 0, 2, 1, 3, 2, 3 है। इन आँकड़ों का बहुलक ज्ञात करें।
उत्तर– दिये गये आँकड़े हैं – 2, 6, 4, 5, 0, 2, 1, 3, 2, 3
| चर के मान | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| बारंबारता | 1 | 1 | 3 | 2 | 1 | 1 | 1 |
उपर्युक्त आँकड़े से स्पष्ट है कि चर 2 की बारंबारता सर्वाधिक अर्थात् 3 है।
अतः बहुलक = 2; Ans.
प्रश्न- निम्नलिखित बारंबारता बंटन का माध्य 50 है, तो लुप्त बारंबारता ‘f’ का मान निकालें।
| वर्ग-अन्तराल | 0 – 20 | 20 – 40 | 40 – 60 | 60 – 80 | 80 – 100 |
| बारंबारता | 17 | f | 32 | 24 | 19 |
उत्तर–
| वर्ग अन्तराल | बारंबारता ( f ) | मध्य बिन्दु ( xi) |
fi xi
|
| 0 – 12 | 17 | 10 | 170 |
| 20 – 40 | f | 30 | 30f |
| 40 – 60 | 32 | 50 | 1600 |
| 60 – 80 | 24 | 70 | 1680 |
| 80 – 100 | 19 | 90 | 1710 |
| ∑fi = 92 + f |
∑fi xi = 5160 + 30f |
माध्य =∑fi xi / ∑fi ⇒ 50 = 5160 + 30f / 92 + f
⇒ 5160 + 30f = 4600 + 50f
⇒ 5160 – 4600 = 50f – 30f
⇒ 560=20f ⇒ f = 560 / 20 = 28
∴ f = 28; Ans.
प्रश्न- 8cm भुजा वाले दो घन बराबर से जोड़ दिये जाते हैं। परिणामी घनाभ का पृष्ठ क्षेत्रफल एवं आयतन ज्ञात करें।
उत्तर– घन की प्रत्येक भुजा = 8 सेमी
चूँकि दो घन समान रूप से जोड़ दिये जाते हैं।
∴ परिणामी घनाभ की लम्बाई = 16cm, चौड़ाई = 8cm, ऊँचाई = 8cm
∴ घनाभ का पृष्टीय क्षेत्रफल = 2(lb + bh + Ih)
= 2(16 x 8 + 8 × 8+16 x 8)
= 2 (128 + 64 + 128)
= 2 × 320 = 640cm2; Ans.
परिणामी घनाभ का आयतन = lbh
= 16 × 8 × 8 = 1024 cm3; Ans.
प्रश्न- एक लम्बवृत्तीय शंकु का आयतन निकालें, जिसकी ऊँचाई 28 cm और आधार की त्रिज्या 21 cm है।
उत्तर– लम्बवृत्तीय शंकु की ऊँचाई = 28 cm तथा त्रिज्या = 21 cm
∴ शंकु का आयतन = 1/3 πr2h = 1/3 x 22/7 x 21 x 21 x 28 = 12936 cm3; Ans
प्रश्न- एक वृत्त के चतुर्थांश का क्षेत्रफल ज्ञात करें जिसकी परिधि 22 cm है।
उत्तर– वृत्त की परिधि = 22 cm
⇒ 2πr = 22 cm ⇒ 2 x 22/7 x r= 22 cm
∴ r = 7 x 22 / 2 x 22 = 7/2cm
∴ वृत्त के चतुर्थांश का क्षेत्रफल= 1/4πr2
= 1/4 x 22/7 x 7/2 x 7/2 = 77/8 cm2Ans.
प्रश्न- 6cm त्रिज्या वाले एक वृत्त के एक त्रिज्यखंड का क्षेत्रफल ज्ञात करें जिसका केन्द्रीय कोण 60° है।
उत्तर– वृत्त की त्रिज्या = 6cm तथा केन्द्रीय कोण = 60°
∴ वृत्त के त्रिज्यखंड का क्षेत्रफल = πr2θ / 360°
= 22/7 x 6 x 6 x 60° / 360
= 132 / 7 cm2; Ans
प्रश्न- बिना विभाजन प्रक्रिया किये बताएँ कि 13/3125 सांत है या असांत ।
उत्तर– 13 / 3125 = p/q
∴ q = 3125 = 5 × 5 × 5 × 5 = 54 = 20 x 54 = 20 x 54
यहाँ q का अभाज्य गुणनखंड 2m x 5n के रूप का है।
∴ 13 / 3125 का दशमलव प्रसार सांत है।
प्रश्न- संख्या 6, 72, और 120 का अभाज्य गुणनखंड विधि द्वारा HCF और LCM ज्ञात करें।
उत्तर– 6 = 2 x 3
72 = 2 x 2 x 2 x 3 x 3 = 23 x 32
तथा 120 = 2 x 2 x 2 x 3 x 5 = 23 x 3 x 5
6, 72, 120 का HCF = 2 x 3 = 6; Ans
6, 72, 120 का LCM = 23 x 32 x 5 = 360; Ans
प्रश्न- बहुपद x3 – 3x2+ x +1 के शून्यक (a – b), a, (a + b) हो तो ‘a’ और ‘b’ का मान ज्ञात करें।
उत्तर– बहुपद x3 – 3x2 + x +1 के शून्यक a – b, a, a + b है।
∴ α = a – b, β = b, y = a + b
दिए गए बहुपद मे, a = 1, b = -3, c = 1 d = 1
∴ α + β + γ = a – b + a + a + b = -b/a = -(-3)/1 = 3
⇒ 3a = 3 ∴ a = 3/3 = 1
पुनः αβ + βγ + γα = (a – b) × a + a (a + b) + (a + b)(a – b)
= c/a = 1/1
⇒ a2 – ab + a2 + ab + a2 – b2 = 1
⇒ 3a2 – b2 = 1 ⇒ 3(1) – b2 = 1
⇒ b2 = 3 – 1 = 2 ∴ b = √2
इस प्रकार a = 1, b = √2; Ans.
प्रश्न- 12. यदि HCF (x, 1428) = 84 एवं LCM (x, 1428) = 244188 है तो x का मान ज्ञात करें।
उत्तर– हम जानते हैं कि दो धनात्मक पूर्णांकों के लिए दोनों संख्याओं का गुणनफल = संख्याओं का LCM x HCF
⇒ x × 1428 = 244188 × 84
⇒ x = 244188 × 84 / 1428 = 171 × 84 = 14364
∴ x= 14364; Ans.
प्रश्न- 5 संतरा और 3 सेबों का मूल्य 35 रु० है तथा 2 संतरा और 4 सेबो का मूल्य 28 रु० है। एक संतरा एवं एक सेब का मूल्य ज्ञात करें।
उत्तर– मान लिया कि एक संतरा का मूल्य = x रु०
तथा एक सेब का मूल्य = y रु०
प्रश्नानुसार, 5x + 3y = 35
2x + 4y = 28
समीकरण (i) में 2 से तथा समीकरण (ii) में 5 से गुणा कर घटाने पर,
10x + 6y = 70
10x + 20y = 140
– – –
—————————
–14y = –70 ∴ y = 5
समीकरण (i) में y का मान रखने पर,
5x + 3y = 35
⇒ 5x + 3 x 5 = 35 = 5x = 35 – 15 = 20
⇒ x = 20 / 5 = 4
अतः एक संतरा का मूल्य = 4 रु०
तथा एक सेब का मूल्य = 5 रु०; Ans.
प्रश्न- प्रतिस्थापन विधि से x + y =14, x – y = 4 का हल करें।
उत्तर– x + y = 14
x – y = 4
समीकरण (i) से, x = 14 – y
अब x का मान समीकरण (ii) में रखने पर,
x – y = 4
⇒ 14 – y – y = 4 = 14 – 2y = 4 ∴ y = 5
∴ x = 14 – y = 14 – 5 = 9
इस प्रकार, x = 9, y = 5; Ans.
प्रश्न- बिन्दुओं ( 3,10) और (6, -8) को जोड़ने वाले रेखाखंड को बिन्दु (-1, 6) किस अनुपात में विभाजित करता है।
उत्तर–
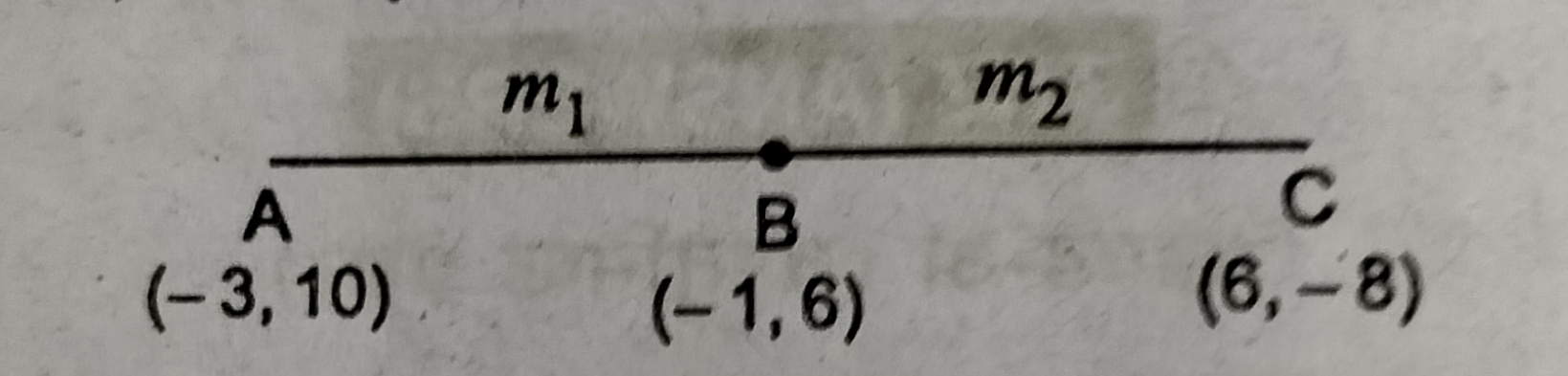
माना कि बिन्दु P( – 1, 6), AB को m1 : m2 में बाँटता है।
∴ AP : PB = m1 : m2
अतः P का x निर्देशांक = m1x2 + m2x1 / m1 + m2
⇒ -1 = m1 x 6 + m1 (-3) / m1 + m2
⇒ – m1 – m2= 6 m1 – 3 m2
⇒ 3 m2 – m2 = 6 m1 + m1
⇒ 2 m2 = 7 m1
⇒ m1 / m2 = 2 / 7 ∴ m 1: m2 = 2 : 7
प्रश्न- y-अक्ष पर एक ऐसा बिन्दु ज्ञात करें जो बिन्दु A (6, 5) और B (- 4, 3) समदूरस्थ है।
उत्तर–
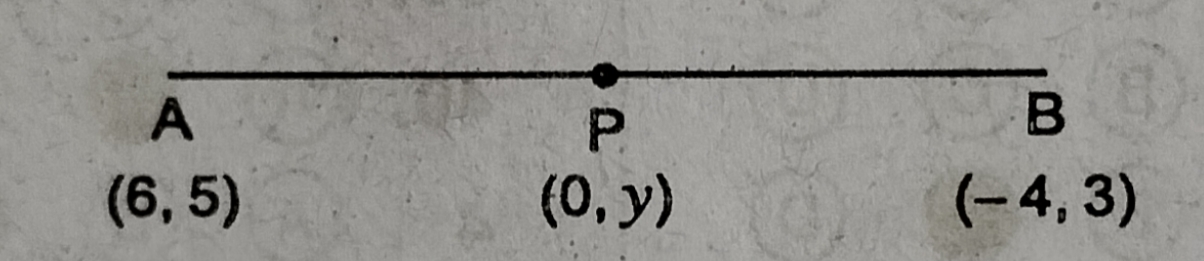
y- अक्ष पर किसी बिन्दु P का निर्देशांक = (0, y)
∴ P का निर्देशांक = (0, y)
चूँकि, P, A एवं B से समदूरस्थ है।
∴ PA = PB ⇒ PA2 = PB2
∴ दूरी सूत्र से, √(0 – 6)2 + (y – 5)2 = √(0 + 4)2 + (y – 3)22
⇒ 36 + y2 – 10y + 25 = 16 + y2 – 6y + 9
⇒ 36 + 25 – 16 – 9 = –6y + 10y
⇒ 36 = 4y
⇒ y = 9
अत: y- अक्ष पर अभीष्ट बिन्दु का निर्देशांक = (0,9); Ans.
प्रश्न- यदि A. B तथा C, ΔABC के अन्तः कोण हों, तो दिखाइए कि tan B + C / 2 = cot A/2
उत्तर– चूँकि A, B एवं C, ΔABC के अन्त: कोण हैं।
∴ A + B + C = 180°
⇒ B + C = 180° – A
⇒ B + C / 2 = 180° – A / 2
⇒ B + C / 2 = 90° – A / 2 (दोनों ओर 2 से भाग देने पर)
∴ tan { B + C / 2 } = tan { 90° – A/2
⇒ tan { B + C / 2 } = cot A/2 ; Proved
प्रश्न- यदि sin(A – B) = 1/2, cos (A + B) = 1/2 तो, A और B का मान ज्ञात करें।
उत्तर– sin (A – B) = 1/2
⇒ sin( A – B) = sin 30°
∴ A – B= 30°
cos( A + B) = 1/2 cos 60°
⇒ A + B = 60°
समीकरण (i) एवं (ii) को जोड़ने पर,
A + B = 30°
A + B = 60°
———————
2A = 90° ∴ A = 45°
समीकरण (ii) में A का मान रखने पर,
A + B = 60°
⇒ 45° + B = 60° ∴ B = 60° – 45° = 15°
इस प्रकार A = 45°, B = 15° ; Ans.
प्रश्न- सिद्ध करें कि वृत्त के बाह्य बिन्दु से खींची गई स्पर्श रेखाओं की लम्बाई समान होती है।
उत्तर– दिया है— वृत्त C (O,r) में एक बाह्य बिन्दु P से वृत्त पर दो स्पर्श रेखाएँ PA एवं PB खींची गई हैं।
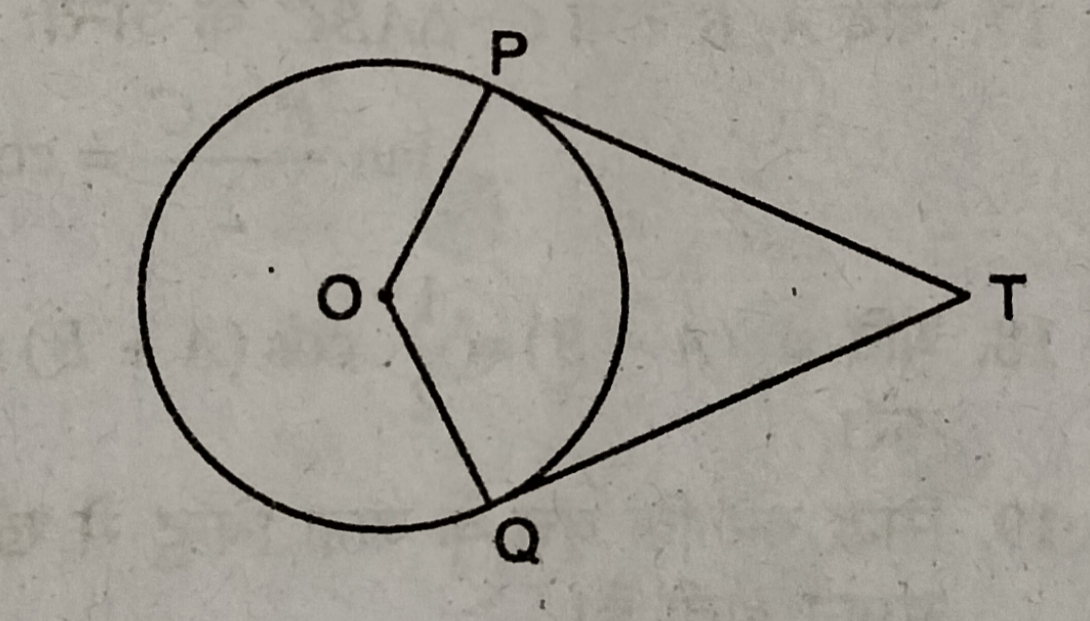
सिद्ध करना है– PA = PB
रचना— OA, OB एवं OP को मिलाया।
प्रमाण– ΔOAP एवं ΔOBP में,
OA = OB (वृत्त की त्रिज्या)
∠OAP =∠OBP = 90°
OP = OP (उभयनिष्ठ)
∴ OAP ≅ OBP (SAS सर्वांगसमता से)
∴ PA = PB (C.P.C.T से) Proved.
प्रश्न- दी गई आकृति में AD ⊥ BC है। सिद्ध करें कि AB2 + CD2 = BD2 + AC2
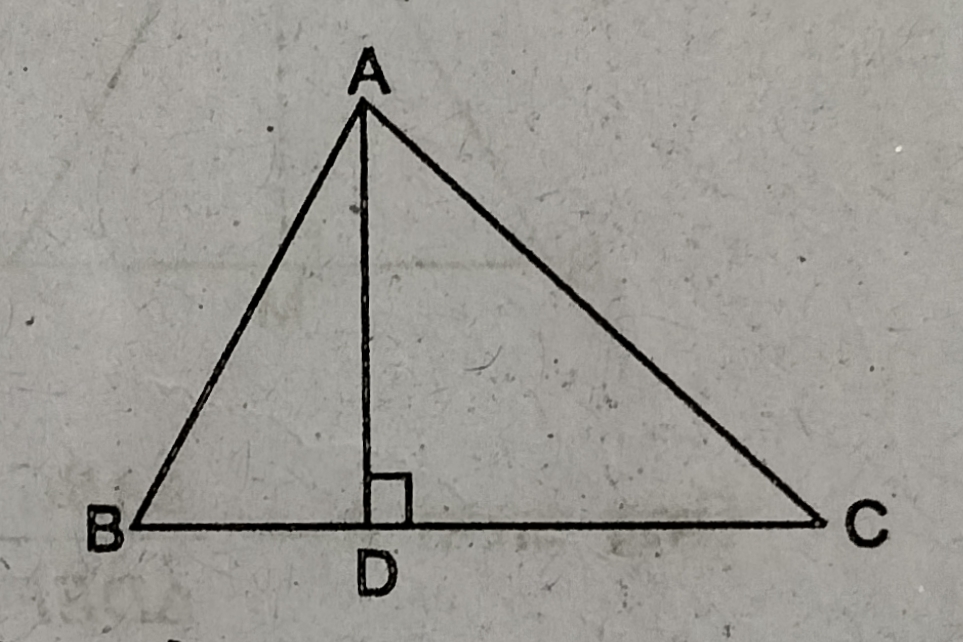
उत्तर– पाइथागोरस प्रमेय से,

ΔADC में,
AC2= AD2+ DC2 …(i)
फिर ADB में,
AB22 = AD2 + DB2 …(ii)
समीकरण (ii) में से समीकरण (i) को घटाने पर,
AB2 – AC2 = DB2 – DC2
⇒ AB2 + DC2 = BD2 + AC2; Proved
प्रश्न- सिद्ध करें कि एक समचतुर्भुज की भुजाओं के वर्गों का योग उनके विकण के वर्गों के योग के बराबर होता है।
उत्तर– ABCD एक समचतुर्भुज है।
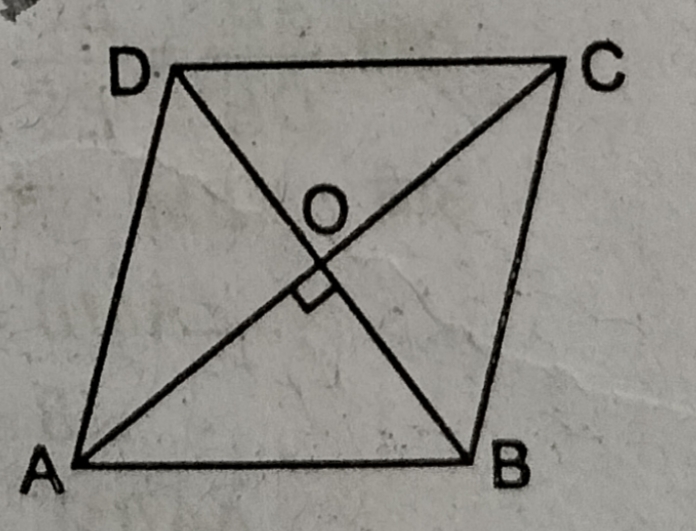
सिद्ध करना है—
AB2 – AC2 = DB2 – DC2
प्रमाण— चूँकि समचतुर्भुज के विकर्ण एक दूसरे को लम्बवत् समद्विभाग करते हैं।
∴ ∠AOB = 90° , OA = OC = 1/2 AC, OB = OD = 1/2 BD
समकोण ΔAOB में, AB2 = OA2 + OB2
⇒ AB2{1/2AC}2 + {1/2BD}2
⇒ AB2 = 1/4 AC2 +1/4BD2
⇒ 4AB2 = AC2+ BD2
⇒ AB2 + AB2+AB2+ AB2 = AC2+ BD2
⇒ AB2 + BC2+CD2+AD2 = AC2 +BD2
समचतुर्भुज ABCD में, AB = BC = CD = AD; proved.
प्रश्न- द्विघात समीकरण 2×22 – 5x + 3 = 0 के मूल पूर्व वर्ग विधि से ज्ञात करें।
उत्तर– 2x2 – 5x + 3 = 0
दोनों ओर 2 से गुणा करने पर,
4x2 – 10x + 6 = 0
⇒ (2x)2 – 2 · 2x· 5/2 + (5/2)2 – (5/2)2 + 6 = 0
⇒ (2x – 5/2)2 – 25/4 + 6 = 0
⇒ (2x – 5/2)2 = 25/4 – 6 = 25 – 24 / 4
⇒ (2x – 5/2)2 = 1/4 = (2x – 5/2) = √1/4
⇒ (2x – 5/2 = ± 1/2
⇒ 2x – 5/2 = 1/2 या, 2x – 5/2 – 1/2
⇒ 2x = 5/2 + 1/2 या, 2x = 5/2 – 1/2 = 5 – 1 / 2
⇒ 2x = 5 + 1 / 2 या, 2x = 4/2 = 2
⇒ 2x = 6/2 = 3 या, x = 2/2
⇒ x = 3/2 या, x = 1
अतः मूल = 3/2, 1; And
प्रश्न- किसी A.P. के प्रथम और अंतिम पद क्रमश: 17 और 350 है। यदि सार्व अन्तर 9 है, तो इसमें कितने पद हैं और इनका योग क्या है ?
उत्तर– A.P. का प्रथम पद (a) = 17
अंतिम पद (l) = 350
सार्व अन्तर (d) = 9
∴ Tn = a + (n – 1) d
⇒ 350 = 17 + (n – 1) 9
⇒ n – 1 = 350 – 17 / 9 = 333 / 9 = 37
∴ n = 37 + 1 = 38 :: पदों की संख्या = 38 Ans.
Sn = n/2 (a + l)
= 38/2 (17 + 350) = 19 x 367 = 6873
अतः 38 पदों का योगफल = 6973; Ans.
प्रश्न- वह समांतर श्रेणी ज्ञात कीजिए जिसका तीसरा पद 5 एवं सातव पद 9 है।
उत्तर– माना कि A.P. का प्रथम पद = a
तथा सार्व अन्तर = d
∴ तीसरा पद = 5 ⇒ a + 2d = 5
एवं सातवाँ पद = 9 ⇒ a + 6d = 9
समीकरण (ii) में से समीकरण (i) को घटाने पर,
a + 6d – a – 2d = 9 – 5 ⇒ 4d = 4 ∴ d = 1
समीकरण (i) से, a + 2d = 5 ⇒ a + 2 x 1 = 5
⇒ a = 5 – 2 = 3
∴ A.P = a, a + d + 2d, a + 3d …
= 3,4,5,6,…Ans
प्रश्न- यदि द्विघात समीकरण 4x2 + px +9=0 के मूल वातविक एवं समन हो तो p का मान ज्ञात करें।
उत्तर– 4x2 + px + 9 = 0
ax2 + bx + c = 0 से तुलना करने पर, a = 4, b = p, c = 9
चूँकि दिये गए समीकरण के मूल समान हैं।
∴ b2 – 4ac = 0
⇒ P2 – 4 x 4 x 9 = 0
⇒ P2 – 144 = 0
⇒ P2 = 144 :: p = ±12; Ans
प्रश्न- पाँच वर्ष पूर्व नूरी के आयु सोनू की आयु की तीन गुनी थी। 10 वर्ष पश्चात्, नूरी की आयु सोनू की आयु की दो गुनी हो जायेगी। नूरी एवं सोनू की वर्तमान आयु ज्ञात करें।
उत्तर– माना कि नूरी की वर्तमान आयु = x वर्ष
एवं सोनू की वर्तमान आयु = y वर्ष
5 वर्ष पहले नूरी की आयु = (x – 5) वर्ष
5 वर्ष पहले नूरी की आयु = (y – 5) वर्ष
प्रश्नानुसार, x – 5 = 3(y – 5)
⇒ x – 5 = 3y – 15
⇒ x – 3y = -15 + 5
⇒ x – 3y = -10
पुनः 10 वर्ष पश्चात् नूरी की आयु = x + 10
एवं सोनू की आयु = y + 10
प्रश्नानुसार, . x + 10 = 2y + 20
⇒ x + 10 = 2y + 20
⇒ x – 2y = 20 – 20
⇒ x – 2y = 10
समीकरण (ii) में से समीकरण (i) को घटाने पर,
x – 2y = 10
x – 3y = – 20
– + +
———————
y = 20 वर्ष
समीकरण (i) में y का मान रखने पर,
x – 3y = – 10
⇒ x – 3 x 20 = -10
⇒ x = 60 – 10 = 50
∴ नूरी की वर्तमान आयु = 50 वर्ष }
सोनू की वर्तमान आयु = 20 वर्ष} ; Ans.
प्रश्न- एक बहुमंजिला भवन के शिखर से देखने पर 8 मीटर ऊँचे भवन के शिखर और तल का अवनमन कोण क्रमश: 30° और 45° है। बहुमंजिला भवन की ऊँचाई एवं दोनों भवनों के बीच की दूरी ज्ञात करें।
उत्तर–
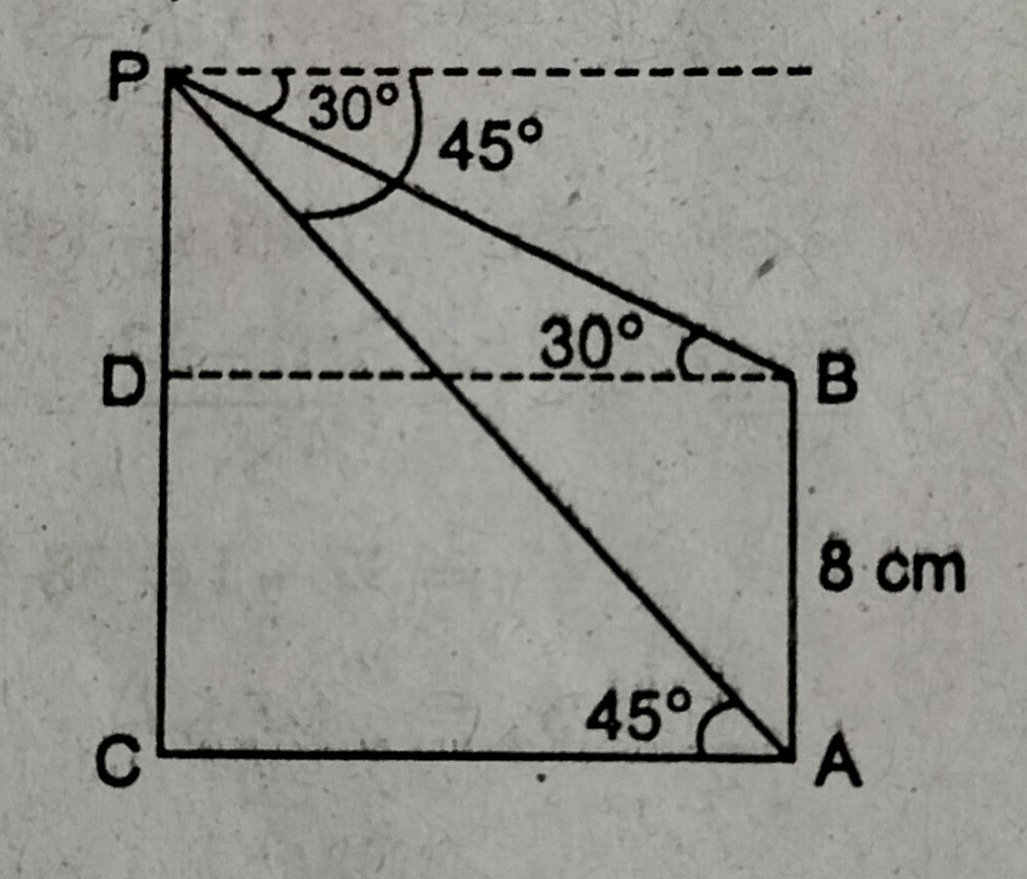
माना कि बहुमंजिला भवन की ऊँचाई = PC
एवं भवन की ऊँचाई = AB = 8m
अब समकोण ΔPBD में,
tan 30 ° = PD / BD
⇒ 1/√3 = PD/ BD
⇒ BD = √3PD
समकोण ΔPAC में,
tan 45° = PC / AC ⇒ 1 = PC / AC ⇒ PC = AC
∴ PC = PD + DC
AC = PD + DC
∴ AC = BD एवं DC = AB = 8m
∴ BD = PD + 8
⇒ √3 PD = PD + 8
⇒ √3PD – PF = 8 = PD (√3 – 1) = 8
∴ PD = 8 / √3 – 1 x √3 + 1 / √3 + 1 = 8√3 + 1) / 2
∴ PD = 4(√3 + 1)
अतः PC = PD +DC = 4√3 + 1) + 8
= 4(√3 + 1 + 2 ) = 4(√3 + 3)m
∴ बहुमंजिला भवन की ऊँचाई =4 (√3 +3)m; Ans.
दोनों भवनों के बीच की दूरी = AC = PC
= 4(√3 + 3) m; Ans
प्रश्न- एक शंकु के छिन्नक जो 45 cm ऊँचा है के सरों की त्रिज्याएँ क्रमशः 28 cm एवं 7 cm हैं। इसका आयतन एवं वक्रपृष्टीय क्षेत्रफल ज्ञात करें।
उत्तर–
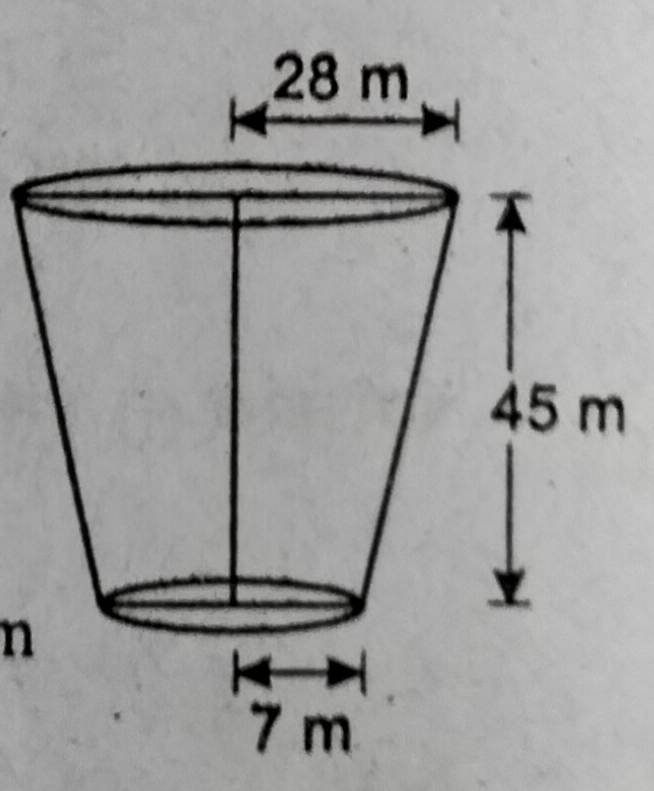
R = 28cm, r7cm, h = 45cm
शंकु के छिन्नक की तिरछी ऊँचाई
I = √h2+ (R – r)2
= √452 + (28 – 7)2 = √452 + 212
I = √2025 + 441 = √2466 = 49.65 cm
अतः बाल्टी की धारिता
= πh / 3 [R2 + Rr + r2]
= 22 x 45 / 7 x 3 [282 + 28 x 7 + 72]
= 22 x 15 / 7 [ 784 + 196 + 49] = 22 x 15 / 7 x 1029
= 22 x 15 x 147 = 48520 cm3; Ans
बाल्टी के वक्रपृष्ठ का क्षेत्रफल
= πI(R + r ) = 22/7 x 49.65 (28 + 7)
= 22/7 x 49.65 x 35 = 22 x 49.65 x 5
= 5462.5 cm2; Ans
प्रश्न- सिद्ध करें कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के अनुपात के बराबर होता है।
उत्तर– दिया गया है – ABC एवं DEF दो समरूप त्रिभुज हैं।
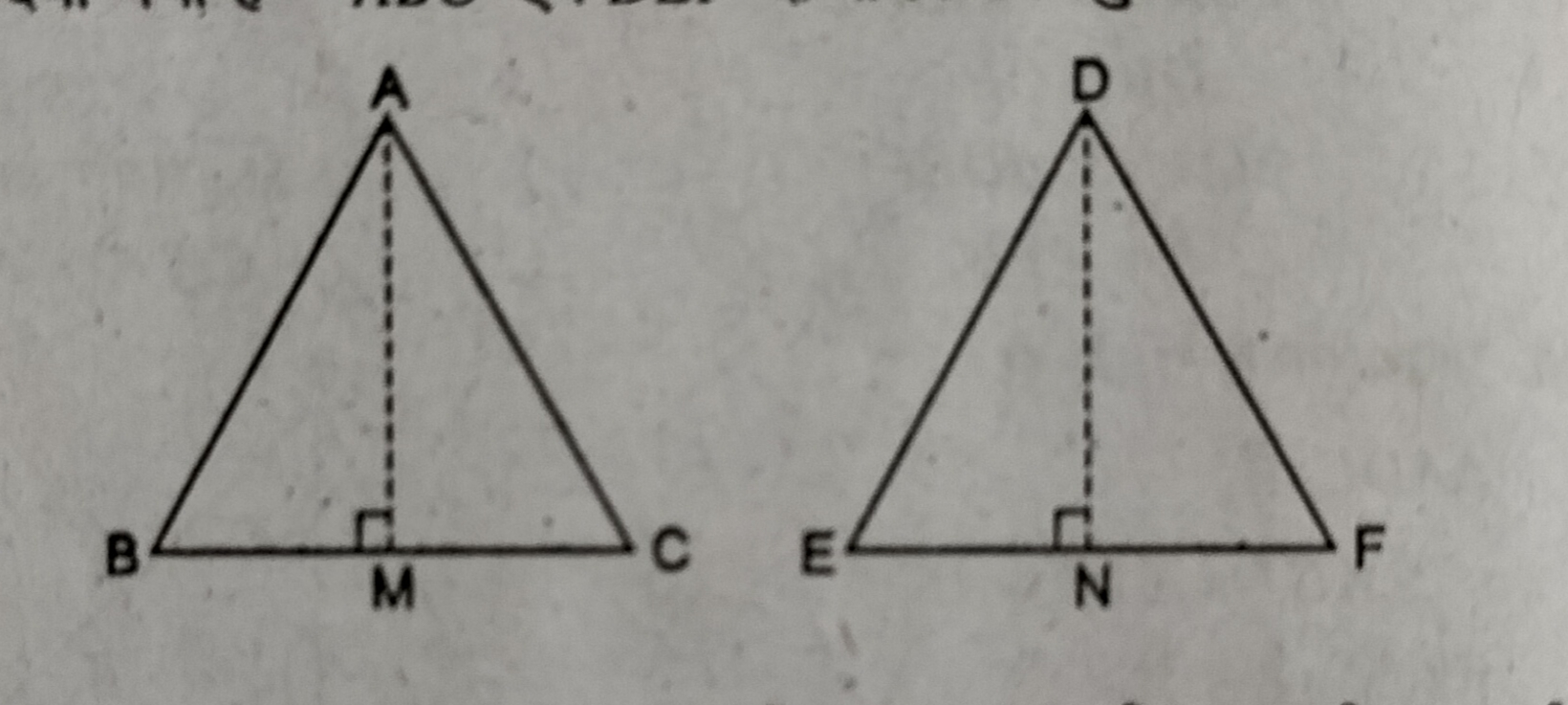
सिद्ध करना है— ΔABC का क्षेत्रफल / ΔDEF का क्षेत्रफल = AB2 / DE2 = BC2 / EF2 = AC2 / DF2
रचना— A से BC पर AM तथा D से EF पर DN लम्ब डाला।
प्रमाण- चूँकि ΔABC ~ ΔDEF
∴ ∠ A = ∠D, ∠B = ∠E, ∠C =∠F
तथा AB/DE = BC/EF = AC/DF या, AB2 / DE2 = BC22 / EF2 = AC22/ DF2
अब ΔABM एवं ΔDEN में,
∠ABM = ∠DEN = 90°
∠B =∠E
∴ ΔABM ~ ΔDEN
∴ AB/DE = AM/DN ⇒ BC/EF = AM/DN
अब ΔABC का क्षेत्रफल / ΔDEF का क्षेत्रफल = 1/2 x BC x AM / 1/2 x EF x DN = BC x AM / EF x DN
= BC / EF x BC / EF
ΔABC का क्षेत्रफल /ΔDEF का क्षेत्रफल = BC2 / EF2
अतः समीकरण (i) एवं (iii) से,
ΔABC का क्षेत्रफल / ΔDEF का क्षेत्रफल = AB2 / DE2 = BC2 / EF2 = AC2 / DF2 ; proved.
प्रश्न- यदि बहुपद p(x) = 2x4 – 3x3 – 5x2 + 9x + 3 के दो (- √3) हों तो शेष शून्यकों का मान ज्ञात करें।
उत्तर– p( x ) = 2x4– 3x3 – 5x2 + 9x – 3
∴ p(x) के दो शून्यक √3 एवं – √3 हैं।
अतः इसके दो गुणनखंड (x – √3 ) एवं (x + √3) होंगे
अतः इन गुणनखंडों का गुणनखंड = (x – √3) (x + √3) = x2 – 3
∴ p(x) के शेष दो गुणनखंड का गुणनफल
= (2x4 – 3x3 – 5x2 + 9x – 3) ÷ (x2 – 3)
अब x2 – 3) 2x4 – 3x3 – 5x2 + 9x – 3 (2x2 – 3x + 1
2x4 – 6x2
– +
—————
-3x3 + x2 + 9x – 3
-3x3. + 9x
+ –
—————————
x2 – 3
x2 – 3
+ –
—————
x
अतः 2x4– 3x3 – 5x2 + 9x – 3 = (x2 – 3) (2x2 – 3x + 1)
शून्यक के लिए p(x) = 0
⇒ (x2 – 3) (2x2 – 3x + 1) = 0
⇒ 2x2 – 3x + 1 = 0 ⇒ (x – 1) (2x – 1) = 0
∴ x = 1, 1/2
अतः p(x) के शेष शून्यक = 1, 1/ 2; Ans.
प्रश्न- यदि किसी भिन्न के अंश एवं हर दोनों में 2 जोड़ दिया जाय तो 9 / 11 हो जाता है। यदि अंश एवं हर दोनों में 3 जोड़ दिया जाय तो वह 5 / 6 हो जाता है। भिन्न ज्ञात करें।
उत्तर– माना कि अभीष्ट भिन्न = x / y
प्रश्नानुसार, x + 2 / y + 2 = 9/11
⇒ 11x + 22 = 9y + 18 ⇒ 11x – 9y = 18 – 22
⇒ 11x – 9y = -4
तथा, x + 3 / y + 3 = 5/6
⇒ 6x + 18 = 5y + 15
⇒ 6x – 5y = -3
समीकरण (i) में 5 से तथा समीकरण (ii) में 9 से गुणा कर घटाने पर,
55x – 45y = -20
54x – 45y = -27
– + +
———————
x = 7
समीकरण (i) में x का मान रखने पर,
11x – 9y = -4 ⇒ 11 x 7 – 9y = -4
⇒ 77 – 9y = -4
⇒ 77 + 4 = 9y ∴ y = 81/9 = 9
अतः अभीष्ट भिन्न = x / y = 7/9; Ans
प्रश्न- ग्राफीय विधि से हल करे— 2x + y = 6; 4x – 2y = 4
उत्तर– दिया गया समीकरण है
2x + y = 6
एवं. 4x – 2y = 4
समीकरण (i) से, y = 6 – 2x
मान सारिणी
| x | 0 | 2 | 3 |
| y | 6 | 2 | 0 |
तथा समीकरण (ii) से,
y = 4x – 4 /2 = 2(2x -2) / 2 ∴ y = 2x – 2
मान सारिणी
| x | 0 | 1 | 2 |
| y | -2 | 0 | 2 |
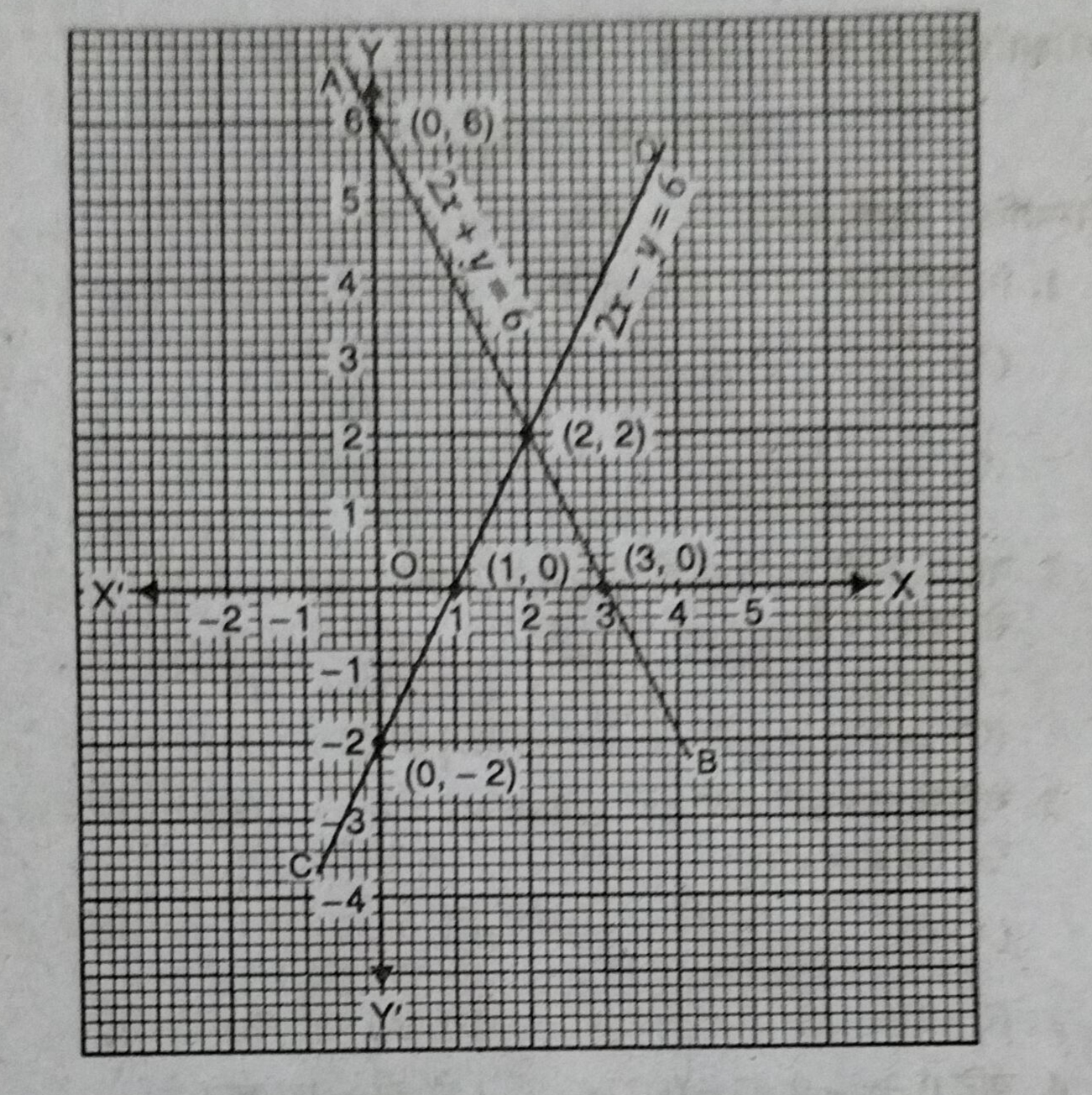
चूँकि दोनों समीकरणों की आलेखी रेखाएँ एक दूसरे को बिन्दु (2, 2) पर प्रतिच्छेद करती हैं। अतः x = 2, y = 2 दिये गए समीकरणों के हल होंगे।
प्रश्न- 6 सेमी, 5 सेमी और 7 सेमी भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ दिये गए त्रिभुज भुजाओं की 3/5 गुनी हो ।
उत्तर– रचना के चरण—
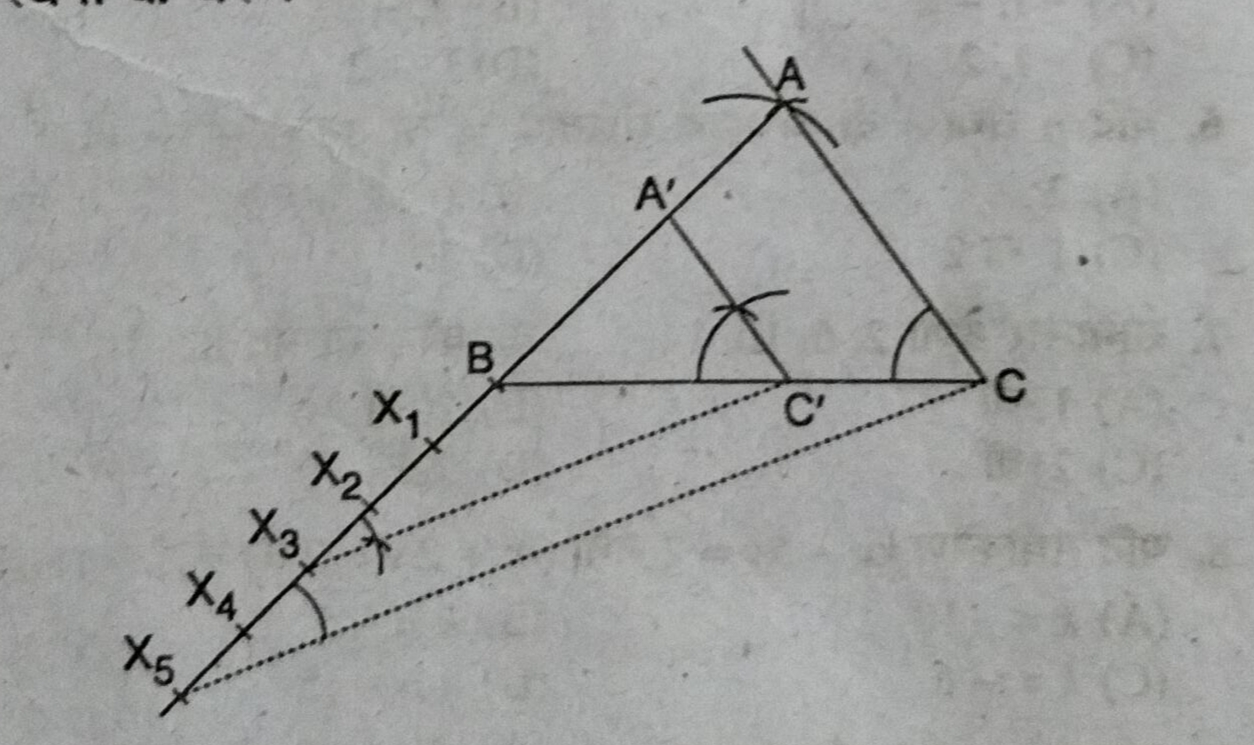
(i) BC = 7cm, की एक रेखा खींचा।
(ii) B से 6 cm त्रिज्या का एक चाप खींचा।
(iii) फिर C से 5cm त्रिज्या का एक चाप खींचा। जो पहले चाप को बिन्दु A पर काटता है।
(iv) A से B तथा A से C को मिलाया।
(v) इस प्रकार ΔABC प्राप्त हुआ।
(vi) AB को आगे की ओर बढ़ाकर उसमें से > BX1 = X1X2= X2X3 = X3X4 = X4X5 काटा।
(vii) X5C को मिलाया । फिर X3 से X5C के सामान्तर एक रेखा खींचा XC जो BC को C’ पर काटता है।
(viii) फिर C’ से CA के समान्तर एक रेखा खींचा जो BA को A’ पर काटता है
(ix) इस प्रकार ΔA’ BC’ प्राप्त हुआ जिसकी भुजाएँ ΔABC की भुजाओं की 3/5 है।
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here