द्रव्यमान केन्द्र एवं घूर्णन गति (Centre of Mass and Rotational Motion)
द्रव्यमान केन्द्र एवं घूर्णन गति (Centre of Mass and Rotational Motion)
द्रव्यमान केन्द्र एवं घूर्णन गति (Centre of Mass and Rotational Motion)
द्रव्यमान केन्द्र (Centre of Mass)
किसी वस्तु में वह बिन्दु जिस पर उसका सम्पूर्ण द्रव्यमान केन्द्रित रहता है, उस वस्तु का द्रव्यमान केन्द्र कहलाता है। अतः द्रव्यमान केन्द्र वह बिन्दु होता है जिस पर पिण्ड का सम्पूर्ण द्रव्यमान केन्द्रित रहता है तथा वस्तु पर लगने वाले सभी बाह्य (संतुलित) बलों को इस बिन्दु पर लगाने पर निकाय / पिण्ड की गति अपरिवर्तित रहती है। यदि कोई निकाय n कणों से मिलकर बना हो, जिनके द्रव्यमान क्रमश: m1, m2, m3, ….., mn तथा इनके स्थिति सदिश क्रमश: r1, r2, r3, …….rn हों, तब निकाय के द्रव्यमान केन्द्र का स्थिति सदिश

द्रव्यमान केन्द्र से सम्बन्धित कुछ महत्वपूर्ण बिन्दु
◆ द्रव्यमान केन्द्र की स्थिति चुने गये निर्देशांक निकाय पर निर्भर नहीं करती।
◆ द्रव्यमान केन्द्र की स्थिति वस्तु के आकार तथा आकृति व द्रव्यमान वितरण पर निर्भर करती है।
◆ सममित वस्तुओं में, यदि द्रव्यमान वितरण एकसमान हो, तो द्रव्यमान केन्द्र, वस्तु के ज्यामितीय केन्द्र के संपाती होता है।
◆ यदि द्रव्यमान केन्द्र मध्यबिन्दु पर स्थित हो तो द्रव्यमान केन्द्र के परितः निकाय के समस्त कणों के द्रव्यमानों के आघूर्णो का योग शून्य होता है।
◆ वस्तु के द्रव्यमान केन्द्र की स्थिति केवल स्थानान्तरीय गति में परिवर्तित होती है, परन्तु घूर्णी गति में परिवर्तित नहीं होती है।
घूर्णन गति (Rotational Motion)
यदि कोई पिण्ड अथवा निकाय किसी स्थिर अक्ष के परितः इस प्रकार गति करता है, कि उसके सभी कण वृत्तीय पथ पर चलते हैं ताकि एक निश्चित समयान्तराल में प्रत्येक कण का कोणीय विस्थापन समान हो, तो उसकी गति को घूर्णन गति कहते हैं। इन समस्त वृत्तीय पथों के केन्द्रों को मिलाने वाली रेखा को घूर्णन अक्ष कहते हैं।
◆ शुद्ध स्थानान्तरीय गति में समय के किसी क्षण पर वस्तु के सभी कण समान वेग से होते हैं।
◆ यदि ऐसा पिण्ड जो किसी निश्चित बिन्दु पर सीमित नहीं है तो ऐसे पिण्ड की गति या तो पूर्णतः स्थानान्तरीय होगी या स्थानान्तरीय व घूर्णन गतियों का संयोजन होगी।
◆ किसी दृढ़ पिण्ड की ऐसी गति, जिसमें पिण्ड की कोई निश्चित रेखा स्थिर रहती है, किन्तु पिण्ड के कण की कोणीय स्थिति समय के साथ परिवर्तित हो, तब इसे निश्चित रेखा के सापेक्ष या परितः उस पिण्ड की घूर्णन गति कहते हैं।
बल आघूर्ण (Torque)
किसी बल की वह प्रवृत्ति जिसके कारण वह एक निश्चित बिन्दु के परितः किसी वस्तु को घुमाने का प्रयास करता है. बल आघूर्ण कहलाता है। बल आघूर्ण का मान वस्तु पर लगे बल के परिमाण तथा निश्चित बिन्दु से बल की क्रिया रेखा की लम्बवत् दूरी के गुणनफल के बराबर होता है। आरोपित बल द्वारा पिण्ड के घूमने की प्रवृत्ति वामावर्त होने पर बल आघूर्ण को धनात्मक चिह्न से तथा दक्षिणावर्त होने पर ऋणात्मक चिह्न द्वारा प्रदर्शित करते हैं।
(बल आघूर्ण, t = F x d)
यहाँ, F = बल तथा d = घूर्णन अक्ष से बल की लम्बवत् दूरी । यह एक सदिश राशि है तथा इसका मात्रक न्यूटन मी होता है।
बल-युग्म (Couple )
किसी वस्तु पर दो बराबर किन्तु विपरीत दिशाओं में कार्य करने वाले समानान्तर बल को बल-युग्म कहते हैं तथा वस्तु पर लगा बल-युग्म सदैव एक दिशीय घूर्णन प्रभाव रखता है।
बल-युग्म का आघूर्ण = बल का मापांक x समान्तर बलों के बीच की दूरी इसका मात्रक न्यूटन मी होता है।
सन्तुलन की अवस्था (Equilibrium of Bodies)
जब किसी वस्तु पर अनेक बल इस प्रकार कार्य कर रहे हों कि वस्तु न तो रेखीय गति करे और न ही घूर्णन गति, तब कहा जाता है कि वस्तु सन्तुलन की अवस्था में है।
सन्तुलन की विभिन्न स्थितियाँ नीचे दी गई हैं
◆ किसी वस्तु पर लगे सभी बलों का सदिश योग शून्य होना चाहिए।
◆ किसी वस्तु पर लगे सभी बलों के आघूर्णों का बीजगणितीय योग शून्य होना चाहिए।
◆ यदि एक कण पर कार्य करने वाले बलों को परिमाण द्वारा दर्शाएँ तथा इनकी दिशाएँ त्रिभुज की तीनों भुजाओं के अनुदिश क्रमानुसार हों, तब ये बल परस्पर सन्तुलन में होंगे।
सन्तुलन के प्रकार (Types of Equilibrium)
सन्तुलन तीन प्रकार के होते हैं
(i) स्थायी सन्तुलन (Stable Equilibrium) यदि किसी वस्तु को उसकी सन्तुलन की अवस्था से थोड़ा-सा विस्थापित करके छोड़ने पर यदि वस्तु पुनः अपनी सन्तुलन की अवस्था को प्राप्त कर लेती है, तो इस प्रकार के सन्तुलन को स्थायी सन्तुलन कहते हैं। इस प्रकार के सन्तुलन में वस्तु की स्थितिज ऊर्जा न्यूनतम होती है। उदाहरण चौड़े आधार पर रखा शंकु। अतः स्थायी सन्तुलन के लिए वस्तु का गुरुत्व केन्द्र अधिक-से-अधिक नीचा होना चाहिए।
(ii) अस्थायी सन्तुलन (Unstable Equilibrium) यदि किसी वस्तु को उसकी सन्तुलन की अवस्था से थोड़ा-सा विस्थापित करके छोड़ने पर वह पुनः सन्तुलन की अवस्था में न आए, तो इस प्रकार के सन्तुलन को अस्थायी सन्तुलन कहते हैं। इस प्रकार के सन्तुलन में वस्तु की स्थितिज ऊर्जा अधिकतम होती है। उदाहरण शीर्ष पर रखा शंकु, नोक पर खड़ी पेन्सिल, अंगुली पर रखी छड़ी।
(iii) उदासीन सन्तुलन (Neutral Equilibrium) यदि किसी वस्तु को उसकी सन्तुलन की स्थिति से थोड़ा-सा विस्थापित करके छोड़ने पर वह वस्तु अपनी पूर्व अवस्था में आने का प्रयास न करे, वल्कि अपनी नई अवस्था में ही सन्तुलित हो जाए, तो इस प्रकार के सन्तुलन को उदासीन सन्तुलन कहते हैं। इस प्रकार के सन्तुलन में वस्तु के गुरुत्व केन्द्र की स्थिति वस्तु की स्थिति बदलने पर नहीं बदलती है। इस प्रकार के सन्तुलन में वस्तु की स्थितिज ऊर्जा नियत होती है।
उदाहरण स्वयं की तिरछी ऊँचाई के सहारे रखा शंकु, गेंद, स्वयं की लम्बाई के सहारे रखा बेलन।
◆ वस्तु की साम्यावस्था या पूर्ण गति निर्देश बिन्दु (reference point) के अभाव के कारण सम्भव नहीं होती है तथा यह निर्देश बिन्दु अन्तरिक्ष में स्थायी रूप से निश्चित होता है।
गुरुत्व केन्द्र (Centre of Gravity)
वह बिन्दु जहाँ पिण्ड का सम्पूर्ण भार केन्द्रित होता है, गुरुत्व केन्द्र कहलाता है। सामान्यतः वस्तु का गुरुत्व केन्द्र इसके द्रव्यमान केन्द्र के साथ मेल खाता है। उदाहरण गोलाकार पिण्ड का गुरुत्व केन्द्र उसके केन्द्र पर स्थित होता है।
◆ यदि वस्तु पृथ्वी के केन्द्र पर होती है, तो केन्द्र पर भी वस्तु का भार शून्य ही होता है।
◆ गुरुत्व केन्द्र के परितः वस्तु के सभी कणों के आघूर्णो का बीजगणितीय योग शून्य होता है।
◆ जब कोई वस्तु विरामावस्था में रहती है, तो इसके गुरुत्व केन्द्र की स्थिति में कोई परिवर्तन नहीं होता। परन्तु यदि वस्तु के आकार अथवा स्वरूप में परिवर्तन होता है, तो उसका गुरुत्व केन्द्र भी बदल जाता है।

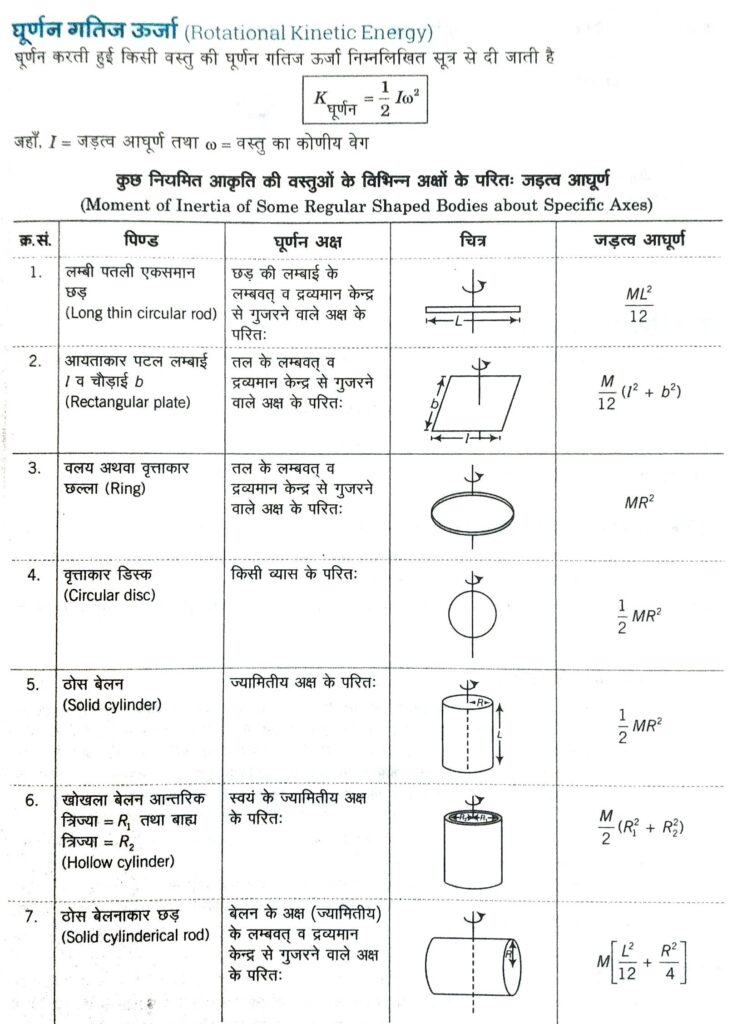
जड़त्व आघूर्ण (Moment of Inertia)
घूर्णन गति में वस्तु का वह गुण जिसके कारण वह किसी अक्ष के सापेक्ष अपनी चूर्णन अवस्था में परिवर्तन का विरोध करती है, उस अक्ष के सापेक्ष वस्तु का जड़त्व आघूर्ण कहलाता है तथा रेखीय गति में द्रव्यमान वही भूमिका निभाता है जो घूर्णन गति में जड़त्व आघूर्ण निभाता है।
घूर्णन गति कर रही किसी वस्तु अथवा कण का किसी अक्ष के सापेक्ष जड़त्व आघूर्ण उस वस्तु अथवा कण के द्रव्यमान व घूर्णन अक्ष से लम्बवत् दूरी के वर्ग के गुणनफल के बराबर होता है। इसे I से प्रदर्शित करते हैं।
अतः (जड़त्व आघूर्ण, I = mr2)
इसका मात्रक किग्रा-मी तथा विमा [ML2 ] होती है।
जड़त्व आघूर्ण का मान घूर्णन अक्ष के सापेक्ष द्रव्यमान, कणों की दूरी व घूर्णन अक्ष की स्थिति पर निर्भर करता है। यहाँ, द्रव्यमान वितरण का तात्पर्य उसके आकार, आकृति व घनत्व से है।
सरल मशीन (Simple Machine)
सरल मशीन एक ऐसी युक्ति है, जिसकी सहायता से किसी बिन्दु पर अधिक बल लगाकर इसे इच्छानुसार दिशा में रोका जा सकता है और सुविधायुक्त गति द्वारा चलाया जा सकता है। इसमें एक लीवर होता है जो गेज, स्क्रू व्हील, एक्सल और पुली आदि को नियन्त्रित करता है।
उत्तोलक (Lever)
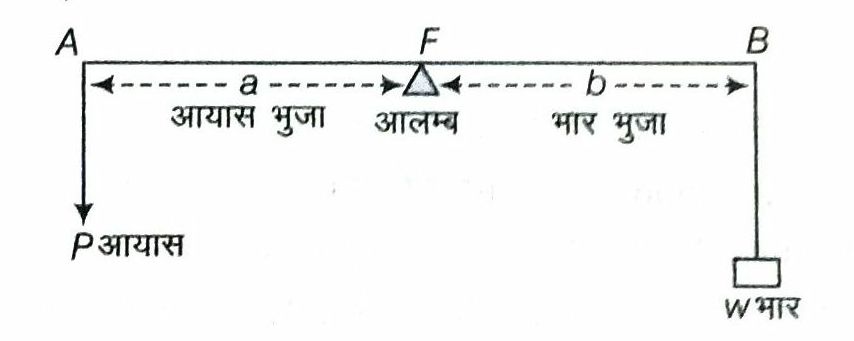
उत्तोलक एक सीधी अथवा मुड़ी हुई दृढ़ छड़ होती है, जो किसी स्थिर बिन्दु के परितः स्वतन्त्रतापूर्वक घूम सकती है। यह एक सरल मशीन है जिसका हम दैनिक जीवन में प्रायः उपयोग करते हैं। इसकी सहायता से किसी भारी बोझ को कम बल लगाकर ही उठाया जा सकता है। उत्तोलक के माध्यम से एक ही बल से भिन्न मापांकों के कार्य संयोजित किए जा सकते हैं। उत्तोलक में तीन मुख्य बिन्दु होते हैं
आलम्ब (Fulcrum) जिस बिन्दु के चारों ओर उत्तोलक स्वतन्त्रतापूर्वक घूम सकता है, उस बिन्दु को आलम्ब कहा जाता है।
आयास (Effort) उत्तोलक द्वारा भारी बोझ को उठाने के लिए आरोपित बल आयास कहलाता है। आलम्ब से आयास की क्रिया – रेखा की लम्बवत् दूरी को आयास-भुजा (effort arm) कहते हैं। भार (Load) उत्तोलक द्वारा जो भारी बोझ उठाया जाता है, भार कहलाता है। आलम्ब से भार की क्रिया-रेखा की दूरी को भार – भुजा (load arm) कहते हैं ।

उत्तोलक के प्रकार (Types of Lever)
उत्तोलक तीन प्रकार के होते हैं
(i) प्रथम वर्ग के उत्तोलक (First Class Lever) इस वर्ग के उत्तोलकों में आलम्ब F, भार w तथा आयास P के बीच में होता है। अतः कम आयास से अधिक भार उठाने के लिए, आयास भुजा (a), भार भुजा (b) से बड़ी होनी चाहिए।
इस वर्ग के उत्तोलकों का यान्त्रिक लाभ 1 से अधिक 1 से कम अथवा 1 के बराबर हो सकता है। कैंची, बोझ उठाने की मुड़ी छड़, कील उखाड़ने का हथौड़ा, प्लास, बच्चों के झूलने का तख्ता (sea-saw), सिण्डासी, नेल कटर, आदि प्रथम वर्ग के उत्तोलक के उदाहरण हैं ।
(ii) द्वितीय वर्ग के उत्तोलक (Second Class Lever) इस वर्ग के उत्तोलकों में भार w, आलम्ब Fतथा आयास P के बीच में होता है। ऐसे उत्तोलकों के लिए a > 6 होने के कारण इनका यान्त्रिक लाभ सदैव 1 से अधिक होता है। इस वर्ग के उत्तोलक की सहायता से कम आयास (P) से, अपेक्षाकृत अधिक भार (w) उठाया जा सकता है। नींबू निचोड़ने की मशीन, सुपारी काटने का सरौता, कूड़ा ढोने की एक पहिए की गाड़ी, नाव खेवते समय नौकादण्ड आदि इस वर्ग के उत्तोलक हैं ।
(iii) तृतीय वर्ग के उत्तोलक (Third Class Lever) इस वर्ग के उत्तोलकों में आयास P, आलम्ब F तथा भार के बीच में होता है। ऐसे उत्तोलकों के लिए a < b होने के कारण इनका यान्त्रिक लाभ सदैव 1 से कम होता है। किसान का हल, चिमटा, सीढ़ी आदि इस वर्ग के उत्तोलक हैं।
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here