Bihar Board Class 9Th Mathematics chapter 14 सांख्यिकी Solutions | Bseb class 9Th Chapter 14 सांख्यिकी Notes
Bihar Board Class 9Th Mathematics chapter 14 सांख्यिकी Solutions | Bseb class 9Th Chapter 14 सांख्यिकी Notes
प्रश्न- उन आंकड़ों के पाँच उदाहरण दीजिए जिन्हें आप अपने दैनिक जीवन से एकत्रित कर सकते हैं।
उत्तर—हल : उन आँकड़ों के उदाहरण जिन्हें हम दैनिक जीवन से एकत्रित कर सकते हैं :
(i) हमारी कक्षा में छात्रों की संख्या ।
(ii) हमारे स्कूल में पंखों की संख्या ।
(iii) हमारे घर का पिछले दो साल का बिजली का बिल ।
(iv) टी. वी. और अखबार से प्राप्त मतदान परिणाम।
(v) शैक्षिक सर्वे से प्राप्त साक्षरता दर के आँकड़े। (और भी विभिन्न उत्तर हो सकते हैं ।)
प्रश्न- ऊपर दिए गए प्रश्न 1 के आंकड़ों को प्राथमिक आंकड़ों या गौण आंकड़ों में वर्गीकृत कीजिए ।
उत्तर— हल : प्राथमिक आंकड़े : (i), (ii) और (iii) गौण आंकड़े : (iv) and (v)
प्रश्न- आठवीं कक्षा के 30 विद्यार्थियों के रक्त समूह इस प्रकार है A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O `A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O इन आंकड़ों को बारंबारता बंटन सारणी के रूप में प्रस्तुत कीजिए। बताइए कि इन विद्यार्थियों में कौन-सा रक्त समूह अधिक सामान्य है और कौन-सा रक्त समूह विरलतम रक्त समूह है।
उत्तर— हल : बारंबारता सारणी निम्न प्रकार है :
| रक्त समूह | विद्यार्थियों की संख्या |
| A | 9 |
| B | 6 |
| O | 12 |
| AB | 3 |
| योग | 30 |
स्पष्ट है कि सबसे अधिक 0 सबसे कम – AB
प्रश्न- तीन सिक्कों को एक साथ 30 बार उछाला गया। प्रत्येक बार चित (Head) आने की संख्या निम्नलिखित है.
| 0 | 1 | 2 | 2 | 1 | 2 | 3 | 1 | 3 | 0 |
| 1 | 3 | 1 | 1 | 2 | 2 | 0 | 1 | 2 | 1 |
| 3 | 0 | 0 | 1 | 1 | 2 | 3 | 2 | 2 | 0 |
ऊपर दिए गए आंकड़ों के लिए एक बारंबारता बंटन सारणी बनाइए।
उत्तर— हल : बारंबारता बंटन सारणी अग्रलिखित प्रकार है :
| चित (Head) की संख्या | बारंबारता |
| 0 | 6 |
| 1 | 10 |
| 2 | 9 |
| 3 | 5 |
| योग | 30 |
प्रश्न- भारतीय समाज के विभिन्न क्षेत्रों में प्रति हजार लड़कों पर लड़कियों की (निकटतम दस तक की) संख्या के आंकड़े नीचे दिए गए हैं:
| क्षेत्र | प्रति हजार लड़कों पर लड़कियों की संख्या |
| अनुसूचित जाति | 940 |
| अनुसूचित जनजाति | 970 |
| गैर अनुसूचित जाति/जनजाति | 920 |
| पिछड़े जिले | 950 |
| गैर पिछड़े जिले. | 920 |
| ग्रामीण | 930 |
| शहरी | 910 |
(i) ऊपर दी गई सूचनाओं को एक दंड आलेख द्वारा निरूपित कीजिए।
(ii) कक्षा में चर्चा करके बताइए कि आप इस आलेख से कौन-कौन से निष्कर्ष निकाल सकते हैं।
उत्तर— हल : (i) वांछित दंड आलेख निम्नलिखित हैं :
समाज की विभिन्न क्षेत्र क्षैतिज x- अक्ष पर तथा प्रति हजार लड़कों पर लड़कियों की संख्या ऊर्ध्वाधर रेखा y- अक्ष पर दर्शाइए। इनका प्रतिच्छेदन बिंदु 900 को दर्शाता है। पैमाना: 1 cm = 10 लड़की ।
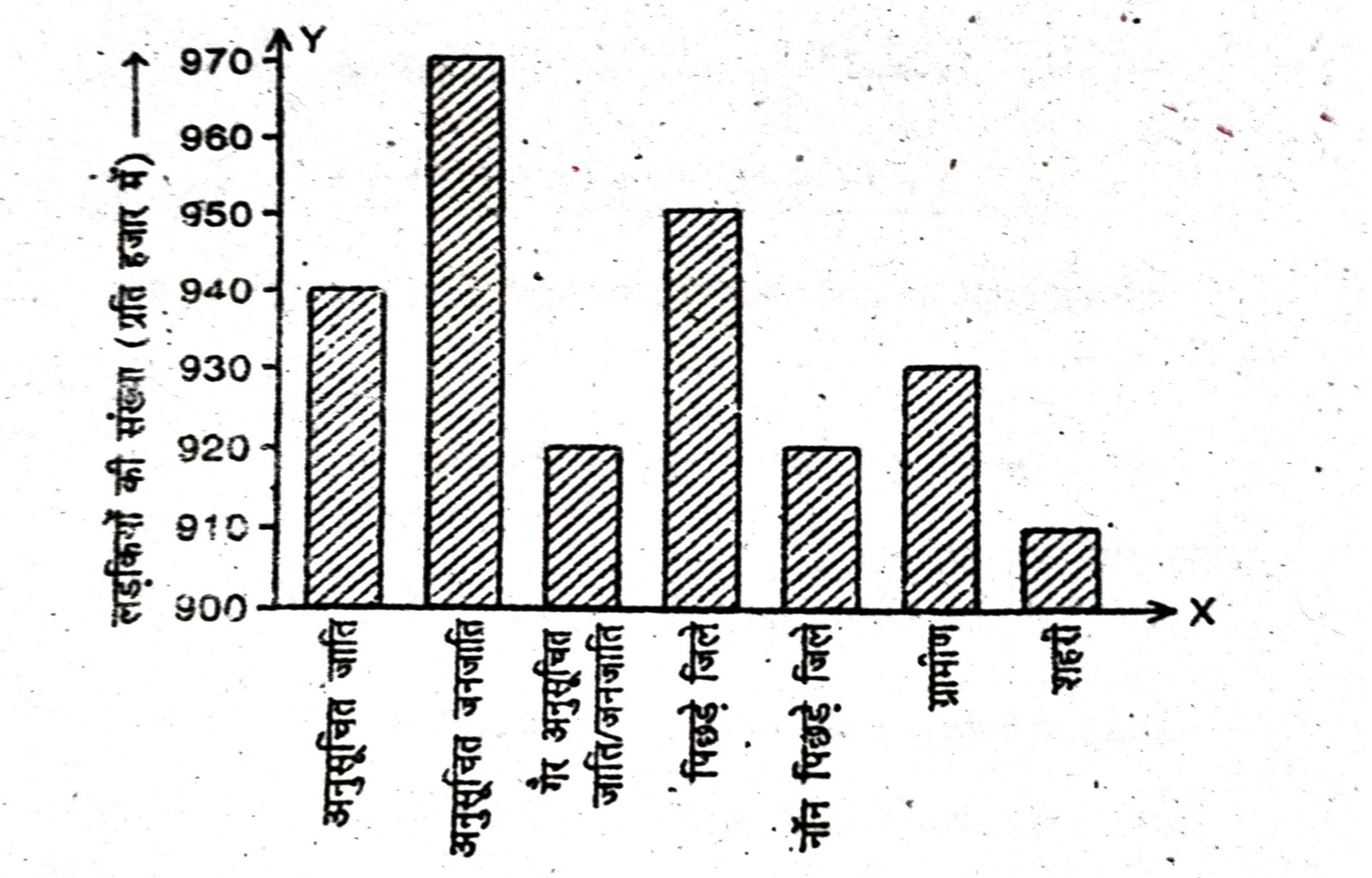
(ii) ग्राफ से हमें ज्ञात होता है कि अनुसूचित जाति में लड़कियों की संख्या प्रति हजार लड़कों पर अधिकतम तथा शहर में न्यूनतम है।
प्रश्न- नीचे की सारणी में 400 नियॉन लैम्पों के जीवन-काल लिए गए है:
| जीवन काल (घंटों में) | लैम्पों की संख्या |
| 300 – 400 | 14 |
| 400 – 500 | 56 |
| 500 – 600 | 60 |
| 600 – 700 | 86 |
| 700 – 800 | 74 |
| 800 – 900 | 62 |
| 900 – 1000 | 48 |
(i) एक आयत चित्र की सहायता से दी हुई सूचनाओं को निरूपित कीजिए।
(ii) कितने लैम्पों के जीवन काल 700 घंटों से अधिक हैं ?
उत्तर— हल: (i) दी गई बारंबारता सारणी का आयत चित्र नीचे दिया गया है :
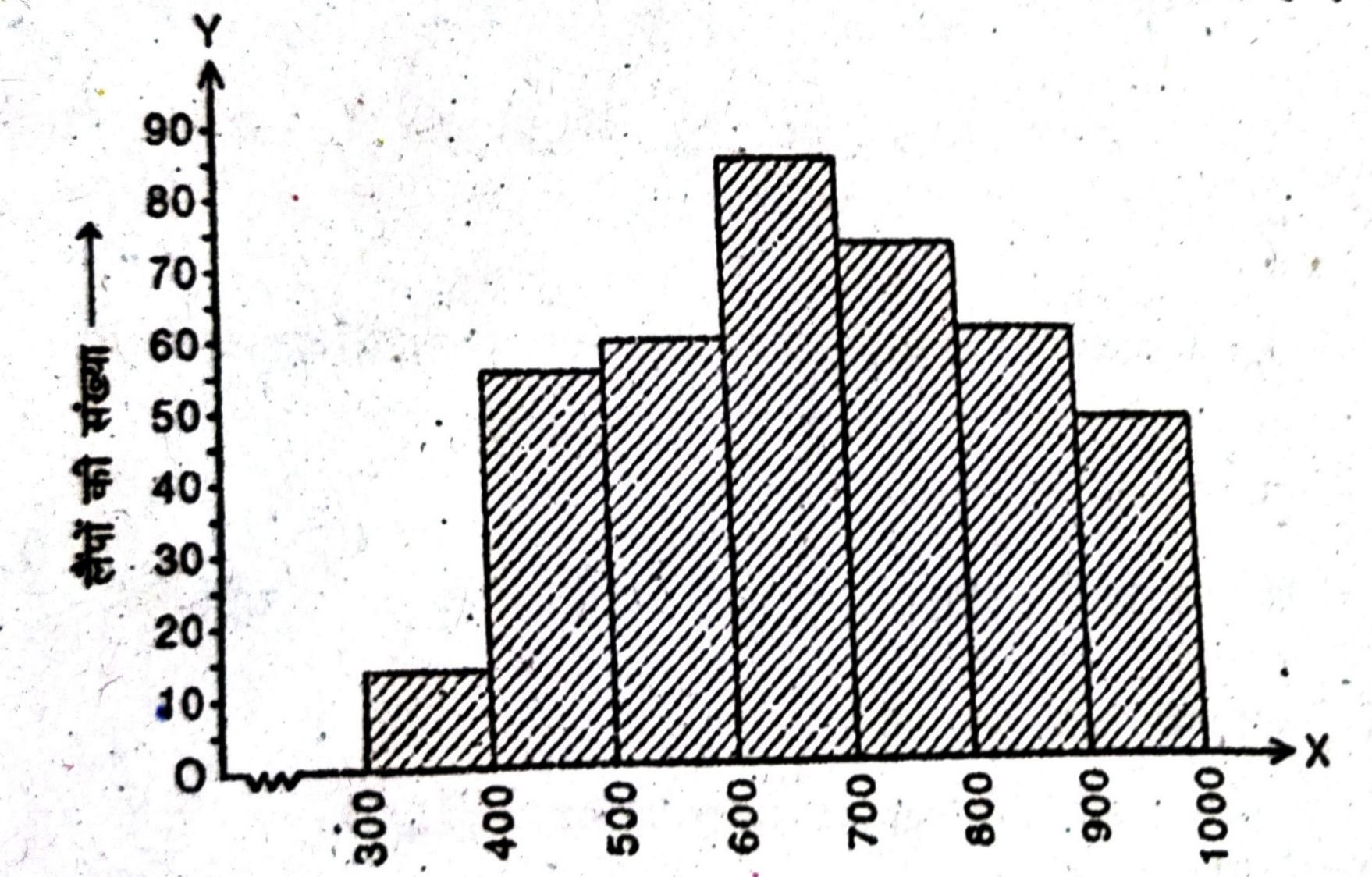
(ii) 700 घंटों से अधिक जीवन काल वाले लैंपों की संख्या 74+62+48 = 184.
प्रश्न- एक टीम ने फुटबाल के 10 मैचों में निम्नलिखित गोल किए : 2, 3, 4, 5, 0, 1, 3, 3, 4, 3 इन गोलों के माध्य, माध्यक और बहुलक ज्ञात कीजिए।
उत्तर— हल : x = X1 + X2 + ……. + x10 का प्रयोग करने पर माध्य
x = 2 + 3 + 4 + 5 + 0 + 1 + 3 + 3 + 4 + 3 / 10 = 28/10 = 2.8
माध्यिका ज्ञात करने के लिए दिये गये आंकड़ों को आरोही क्रम में 0, 1, 2, 3, 3, 3, 4, 4, 5.
यहाँ 10 पद हैं । अतः यहाँ दो मध्य पद होंगे अर्थात् {10)2 और {10/2 + 1}
अर्थात् 5वां और 6ठा पद :
अतः 5वें और 6ठे पद का माध्य माध्यिका होगी ।
अर्थात् माध्यिका = 3 +3 / 2 = 3
पुनः 3 का आंकड़ा सबसे अधिक आया है अर्थात् 4 बार । अतः बहुलक = 3
प्रश्न- आंकड़ों 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14,18 का बहुलक ज्ञात कीजिए ।
उत्तर— हल : दिये आंकड़ों का आरोही क्रम निम्नलिखित प्रकार से प्राप्त होता है :
14, 14, 14, 14, 17, 18, 18, 18, 22, 23, 25, 28. यहाँ 14 सबसे अधिक बार आया है अर्थात् 4 बार
∴ बहुलक = 14.
प्रश्न- निम्न सारणी से एक फैक्ट्री में काम कर रहे 60 कर्मचारियों का माध्य वेतन ज्ञात कीजिए :
| वेतन (रुपयों में) | कर्मचारियों की संख्या |
| 3000 | 16 |
| 4000 | 12 |
| 5000 | 10 |
| 6000 | 8 |
| 7000 | 6 |
| 8000 | 4 |
| 9000 | 3 |
| 10000 | 1 |
| कुल योग | 60 |
उत्तर— हल : माध्य की गणना
|
वेतन (रुपयों में) xi
|
कर्मचारियों की संख्या (fi) | fi xi |
| 3000 | 16 | 48000 |
| 4000 | 12 | 48000 |
| 5000 | 10 | 50000 |
| 6000 | 8 | 48000 |
| 7000 | 6 | 42000 |
| 8000 | 4 | 32000 |
| 9000 | 3 | 27000 |
| 10000 | 1 | 10000 |
| ∑fi= 60 ∑fixi = 305000 |
∴ माध्य = ∑fixi / ∑fi = 5083.33
अतः 60 मजदूरों का माध्य वेतन 5088.33 रुपये है।
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here