Bihar Board Class 9Th Mathematics chapter 5 यूक्लिड की ज्यामिति का परिचय Solutions | Bseb class 9Th Chapter 5 यूक्लिड की ज्यामिति का परिचय Notes
Bihar Board Class 9Th Mathematics chapter 5 यूक्लिड की ज्यामिति का परिचय Solutions | Bseb class 9Th Chapter 5 यूक्लिड की ज्यामिति का परिचय Notes
प्रश्न- निम्नलिखित कथनों में से कौन-से कथन सत्य हैं और कौन-से कथन असत्य हैं ?
(i) एक बिंदु से होकर केवल एक ही रेखा खींची जा सकती है।
(ii) दो भिन्न बिंदुओं से होकर जाने वाली असंख्य रेखाएँ हैं।
(iii) एक सांत रेखा दोनों ओर अनिश्चित रूप से बढ़ाई जा सकती है ।
(iv) यदि दो वृत्त बराबर हैं, तो उनकी त्रिज्याएँ बराबर होती हैं।
उत्तर— (i) असत्य । (ii) असत्य । (iil) सत्य । (iv) सत्य ।
प्रश्न- निम्नलिखित पदों में से प्रत्येक की परिभाषा दीजिए ।
(i) समांतर रेखाएँ (Parallel lines)
(ii) लम्ब रेखाएँ (Perpendicular lines)
(iii) रेखाखंड (Line Segment)
(iv) वृत्त की त्रिज्या (Radius)
(v) वर्ग (Square)
उत्तर— (i) समांतर रेखाएँ— एकही तल में स्थित वे दो रेखाएँ जो किसी भी दिशा में आगे बढ़ाने पर भी एक-दूसरे को नहीं काटती हो, समांतर रेखाएँ कहलाते है।
(ii) लम्ब रेखाएँ— दो रेखाएँ जो आपस में एक-दूसरे पे समकोण बनाते हैं, लम्ब कहलाते है।
(iii) रेखाखंड— दो बिन्दुओं के बीच की निश्चित दूरी जिसे बढ़ाया न जा सके, रेखाखंड कहलाता है।
(iv) वृत्त की त्रिज्या– वृत्त के केन्द्र से परिधि की दूरी को त्रिज्या कहते हैं।
(v) वर्ग— वह चतुर्भुज जिसके चारो भुजाएँ बराबर हो व प्रत्येक कोण समकोण हो, वर्ग कहलाता है।
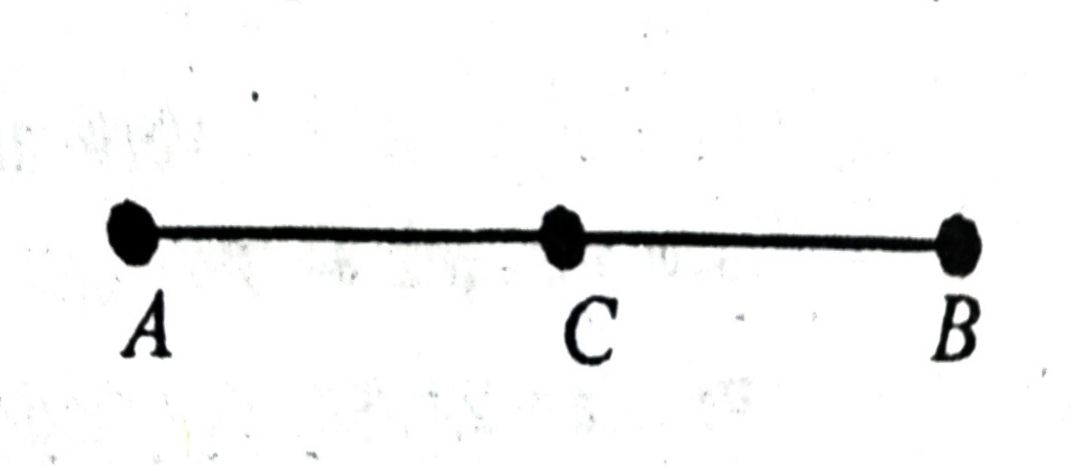
प्रश्न- यदि दो बिंदुओं A और B के बीच एक बिंदु C ऐसा स्थित है कि AC = BC है, तो सिद्ध कीजिए कि AC = 1/2 AB है | एक आकृति खींच AB कर इसे स्पष्ट कीजिए।
उत्तर— हल: हमारे पास एक बिंदु C है जो कि बिंदुओं A तथा B के बीच में इस प्रकार स्थित है कि AC = BC.
दोनों ओर AC जोड़ने पर,
AC + AC = AC + BC
⇒ 2AC = AB [∴ AC + CB, AB के सम्पाती है ]
∴ AC = 1/2 AB
प्रश्न- प्रश्न 4 में, C रेखाखंड AB का मध्य बिंदु कहलाता है। सिद्ध कीजिए कि एक रेखाखंड का एक और केवल एक ही मध्य – बिंदु होता है।
उत्तर— हल माना कि AB का D एक ओर मध्य बिंदु है ।

∴ AD = DB ….(1)
लेकिन दिया गया है कि C, AB का मध्य बिंदु है ।
∴ AC = CB ….(2)
(1) को (2) में से घटाने पर,
AC – AD = CB – DB
⇒ DC = – DC
⇒ 2DC = 0 = DC = 0
∴ C तथा D सम्पाती हैं ।
इस प्रकार, हर एक रेखाखंड का केवल एक ही मध्य बिंदु होता है ।
प्रश्न- यूक्लिड की पाँचो अभिधारणाओं को लिखो :-
उत्तर— अभिधारणा 1: एक बिंदु से दूसरे बिंदु तक सीधी रेखा खींची जा सकती है।
अभिधारणा 2 : एक सांत रेखा को अनिश्चित रूप से बढ़ाया जा सकता है।
अभिधारणा 3 : किसी बिन्दु को केन्द्र मानकर वृत्त खिंचा जा सकता है।
अभिधारणा 4 : सभी समकोण एक-दूसरे के बराबर होते हैं ।
अभिधारणा 5 : यदि कोई सरल रेखा दो अन्य रेखाओं पर गिरकर एक ही ओर दो अन्तः कोण जिनका योग 180° से कम हो बनानी है तो ये दो रेखा उसी दिशा में एक-दूसरे को काटंगी जिधर अन्तः कोण है।
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here