Bihar Board Class 9Th Mathematics chapter 7 त्रिभुजSolutions | Bseb class 9Th Chapter 7 त्रिभुज Notes
Bihar Board Class 9Th Mathematics chapter 7 त्रिभुजSolutions | Bseb class 9Th Chapter 7 त्रिभुज Notes
प्रश्न- ABCD एक चतुर्भुज है, जिसमें AD= BC और ∠DAB = ∠CBA है (आकृति देखें)। सिद्ध कोजिए कि
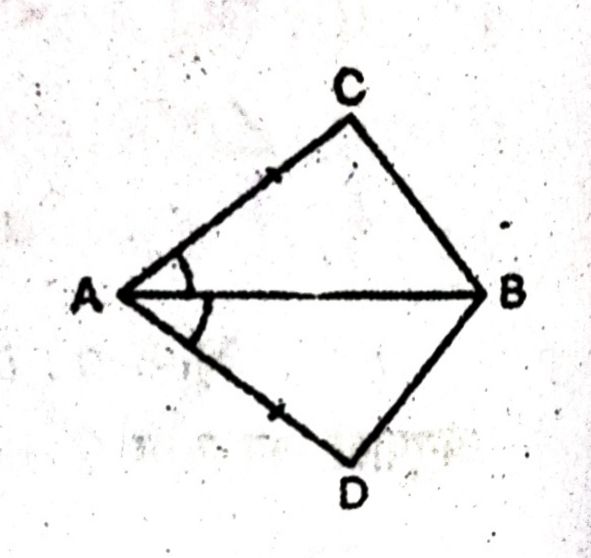
(i) ΔABD ≅ BAC (ii) BD = AC (iii) ∠ABD = ∠BAC
उत्तर— हल : ΔABD तथा ΔBAC में,
AD = BC [दिया है]
∠DAB = ∠CBA [दिया है]
AB = AB [उभयनिष्ठ]
∴ भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से,
ΔABD = ΔBAC. [जिससे सिद्ध होता है]
⇒ BD = AC
और, ∠ABD = ∠BAC [∴ सर्वांगसम त्रिभुज के संगत भाग बराबर होते हैं]
प्रश्न- एक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं (देखिए आकृति) । दर्शाइए कि CD, रेखाखंड AB को समद्विभाजित करता है ।
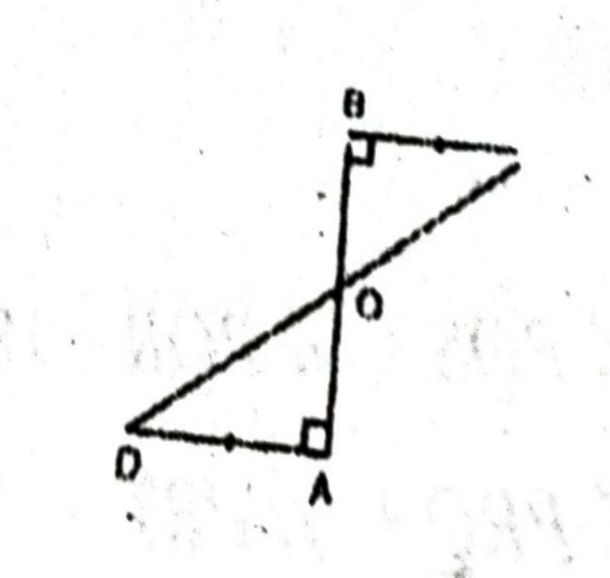
उत्तर— हल : क्योंकि AB और CD, O पर प्रतिच्छेद करते हैं। इसलिए
∠AOD = ∠BOC …(1) [शीर्षाभिमुख कोण]
∠AOD और ∠BOC में,
∠AOD = ∠BOC [1 से]
∠DAO = ∠OBC [प्रत्येक 90°]
AD = BC [दिया है]
∴ अब कोण-कोण-भुजा सर्वांगसम गुणधर्म से,
ΔAOD ≅ ΔBOC
⇒ OA = OB [∴ सर्वांगसम त्रिभुजों के संगत भाग बराबर होते हैं]
प्रश्न- I और m दो समांतर रेखाएँ हैं जिन्हें समांतर रेखाओं p और q का एक अन्य युग्म प्रतिच्छेदित करता है (देखिए आकृति) । दर्शाइए कि ΔABC= ΔCDA है।
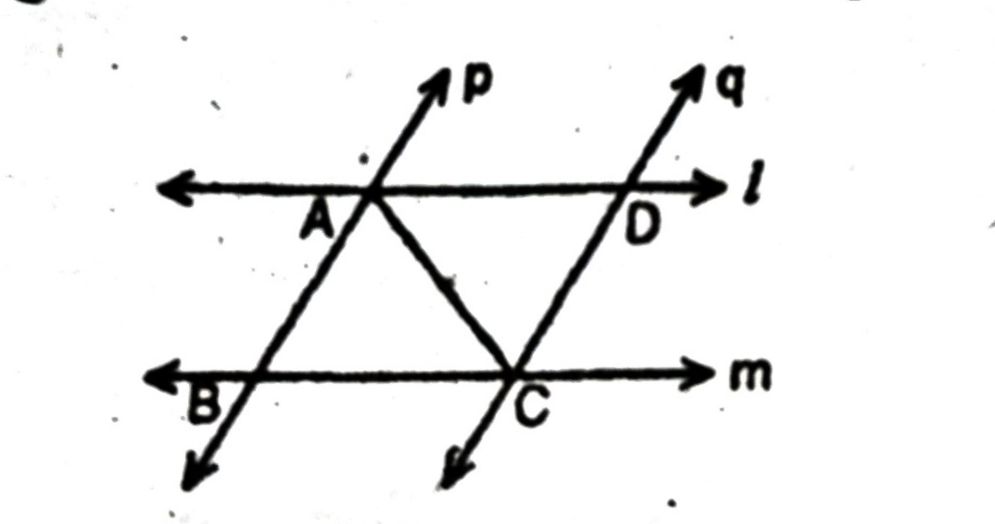
उत्तर— हल : चूँकि I तथा m समांतर रेखाएँ दूसरी समांतर रेखाओं p और q द्वारा प्रतिच्छेदित की जाती हैं । अतः AD || BC तथा AB || CD
⇒ ABCD समांतर चतुर्भुज हैं ।
अत: AB = CD और BC = AD
अब ΔABC और ΔCDA में,
AB = CD [ ऊपर प्रमाणित किया गया है]
BC = AD [ऊपर प्रमाणित किया गया है]
तथा AC = AC [उभयनिष्ठ]
∴ भुजा- भुजा- भुजा सर्वांगसमता गुणधर्म से, ΔABC ≅ ΔCDA.
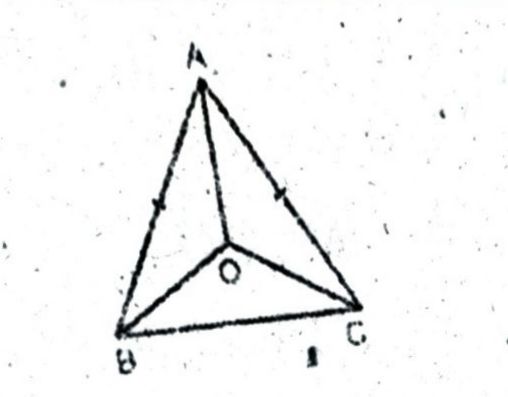
प्रश्न- एक समद्विबाहु त्रिभुज ABC जिसमें AB = AC हैं, ∠B और ∠C के समद्विभाजक परस्पर बिंदु पर प्रतिच्छेद करते हैं A को 0 से जोड़िए । दर्शाइए कि
(i) OB = OC (ii) A0 कोण 4 को समद्विभाजित करता है।
उत्तर— हल : (i) ΔABC में, AB = AC, ∠B = ∠C
[∴ बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।]
⇒ 1/2 ∠B = 1/2 ∠C
⇒ ∠OBC = ∠OCB ……(1)
[∴ OB तथा OC क्रमश: B तथा C को काटते हैं]
∴ ∠OBC = 1/2 ∠B और ∠OCB = 1/2 ∠C
OB = OC ……(2)
[समान कोणों की सम्मुख भुजाएँ समान होती हैं।]
(ii) अब ΔABO तथा ΔACO में,
AB = AC [दिया है]
∠OBC = ∠OCB [समीकरण 1 से]
OB = OC [समीकरण 2 से]
∴भुजा – कोण – भुजा सर्वांगसमतां गुणधर्म से,
ΔABO ≅ ΔACO ⇒ ∠BAO = ∠CAO
[∴ सर्वांगसम त्रिभुजों के संगत भागं बराबर होते हैं ]
⇒ AO, ∠BAC को समद्विभाजित करता है ।
प्रश्न- BE और CE एक त्रिभुज ABC के दो बराबर शीर्षलम्ब हैं। RHS सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है।
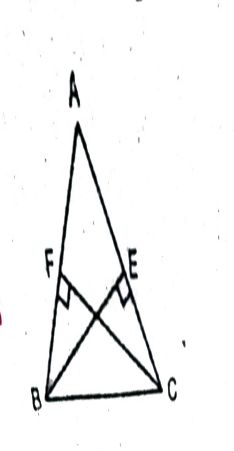
उत्तर— हल : ΔBCF तथा ΔCBE में,
∠BFC = ∠CEB [ प्रत्येक = 90°]
कर्ण BC = कर्ण BC [उभयनिष्ठ]
FC = EB
∴ समकोण कर्ण भुजा सर्वांगसमता गुणधर्म से,
ΔBCF ≈ ΔCBE
⇒ ∠FBC = ∠ECB
[∴ सर्वांगसम त्रिभुज के संगत भाग बराबर होते हैं। ABC एक समद्विबाहु त्रिभुज है।
प्रश्न- दर्शाइए कि समकोण त्रिभुज में कर्ण सबसे लंबी भुजा होती है।
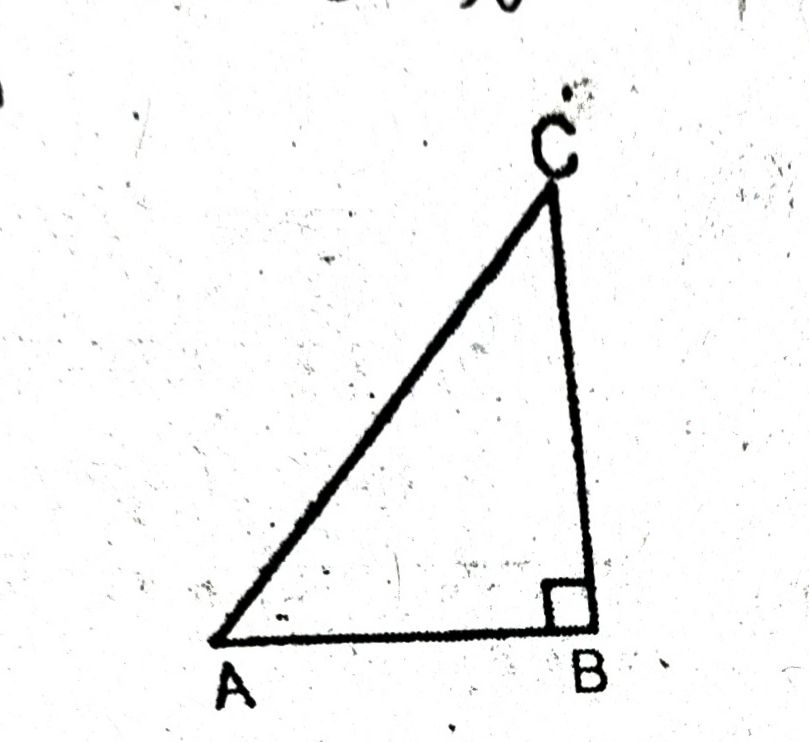
उत्तर— हल : माना कि ΔABC समकोण त्रिभुज है जिसमें ∠ABC = 90°
लेकिन ∠ABC + ∠BCA + ∠CAB = 180°
90° + ∠BCA + ∠CAB = 180°
∠BCA + ∠CAB = 90°
∠BCA तथा ∠CAB न्यून कोण हैं ।
∠BCA < 90° तथा ∠CAB < 90°
AC > AB तथा AC > BC
[∴ बड़े कोण के सम्मुख भुजा बड़ी होती है]
प्रश्न- आकृति में, ∠B < ∠A और ∠C < ∠D है। दर्शाइए कि AD < BC है।
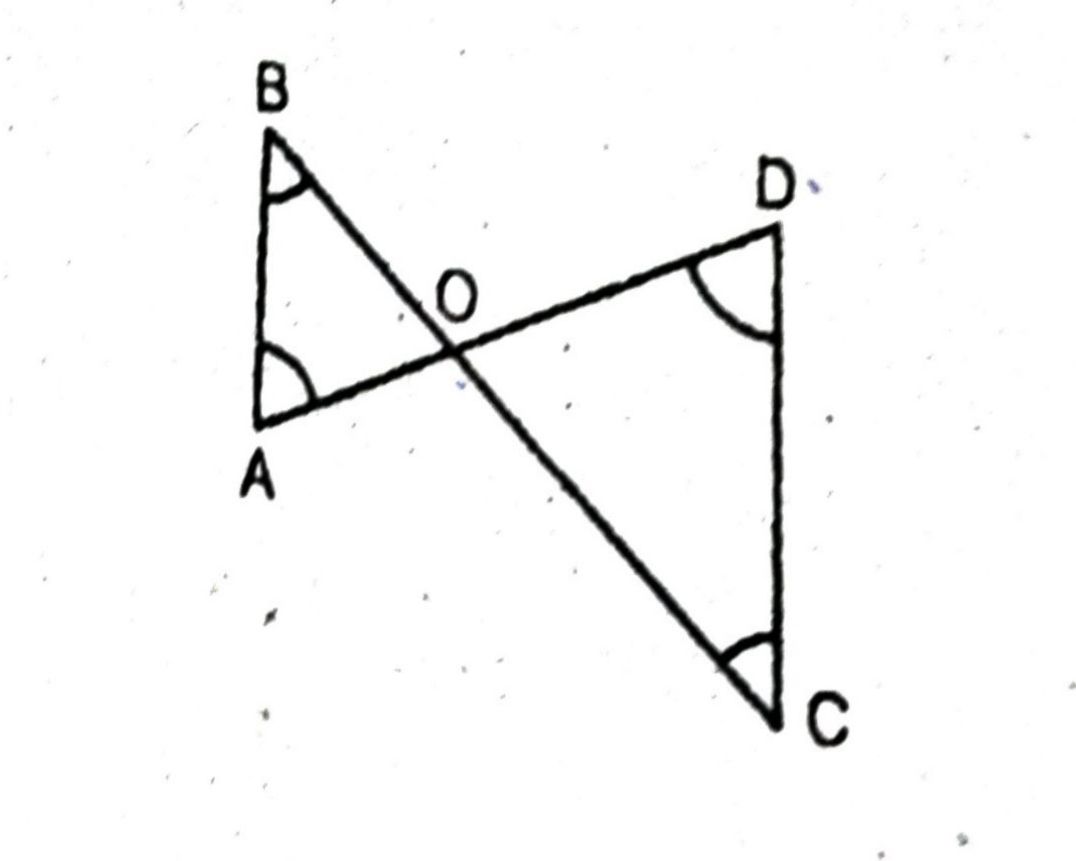
उत्तर— हल चूँकि : ∠B < ∠A तथा ∠C < ∠D
∴ AO < BO और OD < OC
[∴ बड़े कोण की सम्मुख भुजा बड़ी होती है।
इन परिणामों को जोड़ने पर,
AO – OD < BO + OC
⇒ AD < BC
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here