मात्रक, मापन तथा त्रुटि (Units, Measurements and Errors)
मात्रक, मापन तथा त्रुटि (Units, Measurements and Errors)
मात्रक, मापन तथा त्रुटि (Units, Measurements and Errors)
भौतिक राशियाँ (Physical Quantities)
जिसे संख्या के रूप में प्रकट किया जा सके, उसे राशि ( quantity) कहते हैं। उदाहरण जनसंख्या, वस्तु की लम्बाई, प्रतिशत, वस्तु का भार, अंक, आदि। भौतिकी के नियमों को जिन राशियों के पदों में व्यक्त किया जाता है, उन्हें भौतिक राशियाँ कहते हैं। उदाहरण लम्बाई, ताप, द्रव्यमान, समय, दाब, बल, वेग, चाल, दूरी, विद्युत धारा, संवेग, घनत्व, आदि।
भौतिक राशियों के प्रकार (Types of Physical Quantities)
I. मात्रक तथा मापन के आधार पर
(i) मूल राशियाँ (Fundamental or Base Quantities) वे राशियाँ, जो अन्य राशियों से स्वतन्त्र (independent) होती हैं तथा जिन्हें व्यक्त (describe) करने के लिए अन्य भौतिक राशियों की आवश्यकता नहीं होती है, मूल राशियाँ कहलाती हैं।
मूल भौतिक राशियाँ सात प्रकार की होती हैं
लम्बाई, समय, ताप, द्रव्यमान, विद्युत धारा, ज्योति तीव्रता तथा पदार्थ की मात्रा।
(ii) व्युत्पन्न राशियाँ (Derived Quantities) वे राशियाँ, जो मूल राशियों की सहायता से प्राप्त होती हैं, व्युत्पन्न राशियाँ कहलाती हैं।
उदाहरण क्षेत्रफल, आयतन, दाब, चाल, वेग, त्वरण, बल, कार्य, ऊर्जा, आदि ।
(iii) पूरक राशियाँ (Supplementary Quantities) मूल राशियों तथा व्युत्पन्न राशियों के अतिरिक्त दो अन्य भौतिक राशियाँ भी होती हैं, जो ना ही मूल राशियाँ होती है और ना ही व्युत्पन्न। ये राशियाँ पूरक राशियाँ कहलाती हैं। समतल कोण तथा घन कोण दो पूरक राशियाँ हैं।
II. दिशा तथा परिमाण के आधार पर
(i) अदिश राशियाँ (Scalar Quantities) वे भौतिक राशियाँ, जिन्हें व्यक्त करने के लिए केवल परिमाण (magnitude) की आवश्यकता होती है दिशा की नहीं, अदिश राशियाँ कहलाती हैं। जैसे दूरी, चाल, द्रव्यमान, आयतन, घनत्व, कार्य, ताप, विद्युत धारा, समय, ऊर्जा, शक्ति, दाब, आवृत्ति, आवेश, ऊष्मा, विभव, विशिष्ट ऊष्मा, आदि।
(ii) सदिश राशियाँ (Vector Quantities) वे भौतिक राशियाँ, जिन्हें व्यक्त करने के लिए परिमाण के साथ-साथ दिशा की भी आवश्यकता होती है, सदिश राशियाँ कहलाती हैं। उदाहरण विस्थापन, वेग, त्वरण, बल, संवेग, आवेग, भार, बल-आघूर्ण, कोणीय वेग, वैद्युत क्षेत्र, चुम्बकीय क्षेत्र, चुम्बकन तीव्रता, चुम्बकीय आघूर्ण, विद्युत तीव्रता, आदि।
मापन (Measurement )
किसी भौतिक राशि का उसके निश्चित मानक से तुलनात्मक अध्ययन ही मापन कहलाता है। इसमें परिमाण व्यक्त करने के लिए केवल पूर्णांक का प्रयोग नहीं किया जाता, बल्कि मापक यन्त्र का प्रयोग करके ही भौतिक राशि का परिमाण ज्ञात किया जाता है।
प्रत्येक भौतिक राशि के मापन के लिए निम्न दो कारकों की आवश्यकता होती है
(i) भौतिक राशि का आंकिक मान अर्थात् परिमाण यह एक शुद्ध संख्या होती है।
(ii) भौतिक राशि को मापने के लिए स्वेच्छा से चुना गया मानक अर्थात् मात्रक
मात्रक (Units)
प्रत्येक भौतिक राशि को मापने के लिए स्वेच्छा से चुने गए किसी निश्चित परिमाण को मात्रक कहते हैं।
उदाहरण – बल (F) = 10 x 1 न्यूटन = 10 न्यूटन
यहाँ. 10 दर्शाता है कि 10 न्यूटन बल लिए गए मात्रक ( 1 न्यूटन) का 10 गुना है।
मात्रकों को निम्नलिखित भागों में विभाजित किया जाता है
मूल मात्रक (Fundamental or Base Units)
मूल राशियों के मात्रक मूल मात्रक कहलाते हैं या वे मात्रक, जो स्वतन्त्र होते हैं अर्थात् जो अन्य मात्रकों पर निर्भर नहीं करते हैं, मूल मात्रक कहलाते हैं। मूल मात्रक सात प्रकार के होते हैं
मीटर, किलोग्राम, सेकण्ड, ऐम्पियर, केल्विन, केण्डिला तथा मोल।
इन मात्रकों का उपयोग भौतिक राशियों के मानकों के लिए जाता है तथा ये एक-दूसरे से स्वतन्त्र होते हैं। प्रारम्भ में, केवल मीटर, किलोग्राम तथा सेकण्ड ही मुक्त मात्रक होते थे लेकिन बाद में ऐम्पियर (विद्युत धारा), केल्विन (ताप), केण्डिला (ज्योति तीव्रता) तथा मोल ( पदार्थ की मात्रा) के मात्रकों को मूल मात्रकों में शामिल कर लिया गया।
व्युत्पन्न मात्रक (Derived Units)
मूल राशियों के अतिरिक्त अन्य सभी राशियों के मात्रकों को व्युत्पन्न मात्रक कहते हैं जो मूल मात्रकों की सहायता से प्राप्त किए जाते हैं।
उदाहरण क्षेत्रफल, आयतन, घनत्व, चाल, शक्ति, कार्य, बल, ऊर्जा, त्वरण, संवेग के मात्रक, आदि।
पूरक मात्रक (Supplementary Units)
वे मात्रक जिनका उपयोग पूरक राशियों में किया जाता है, पूरक मात्रक कहलाते हैं। पूरक मात्रक न ही मूल मात्रक हैं और न ही व्युत्पन्न मात्रक हैं। समतल कोण (plane angle) तथा घन कोण (solid angle) के मात्रक पूरक मात्रक हैं।
मात्रकों की पद्धति (System of Units)
मूल मात्रकों तथा व्युत्पन्न मात्रकों का समूह मात्रकों की पद्धति कहलाता है। मात्रकों की मुख्य पद्धतियाँ निम्न प्रकार हैं
(i) MKS पद्धति (मीटर किलोग्राम सेकण्ड)
इस पद्धति में लम्बाई का मात्रक मीटर, द्रव्यमान का मात्रक किलोग्राम तथा समय का मात्रक सेकण्ड होता है।
(ii) CGS पद्धति (सेमी ग्राम सेकण्ड)
इस पद्धति में लम्बाई का मात्रक सेमी, द्रव्यमान का मात्रक ग्राम तथा समय का मात्रक सेकण्ड होता है। इस पद्धति को गॉसियन पद्धति भी कहते हैं।
◆ MKS तथा CGS पद्धति को क्रमशः मीट्रिक तथा डेसीमल पद्धति कहते हैं।
(iii) FPS पद्धति (फुट पाउण्ड सेकण्ड )
इस पद्धति में लम्बाई का मात्रक फुट, द्रव्यमान का मात्रक पाउण्ड तथा समय का मात्रक सेकण्ड होता है। इस पद्धति को ब्रिटिश पद्धति भी कहते हैं।
(iv) अन्तर्राष्ट्रीय मात्रक पद्धति (SIUnits)
1960 में माप तौल की अन्तर्राष्ट्रीय समिति ने मात्रकों की एक पद्धति निश्चित की, जिसे मात्रकों की अन्तर्राष्ट्रीय पद्धति कहते हैं तथा संक्षेप में इसे SI मात्रक से प्रदर्शित करते हैं। यह प्रणाली MKS पद्धति का सुधरा हुआ रूप है। इस पद्धति में सात मूल राशियाँ तथा दो पूरक राशियाँ होती हैं।
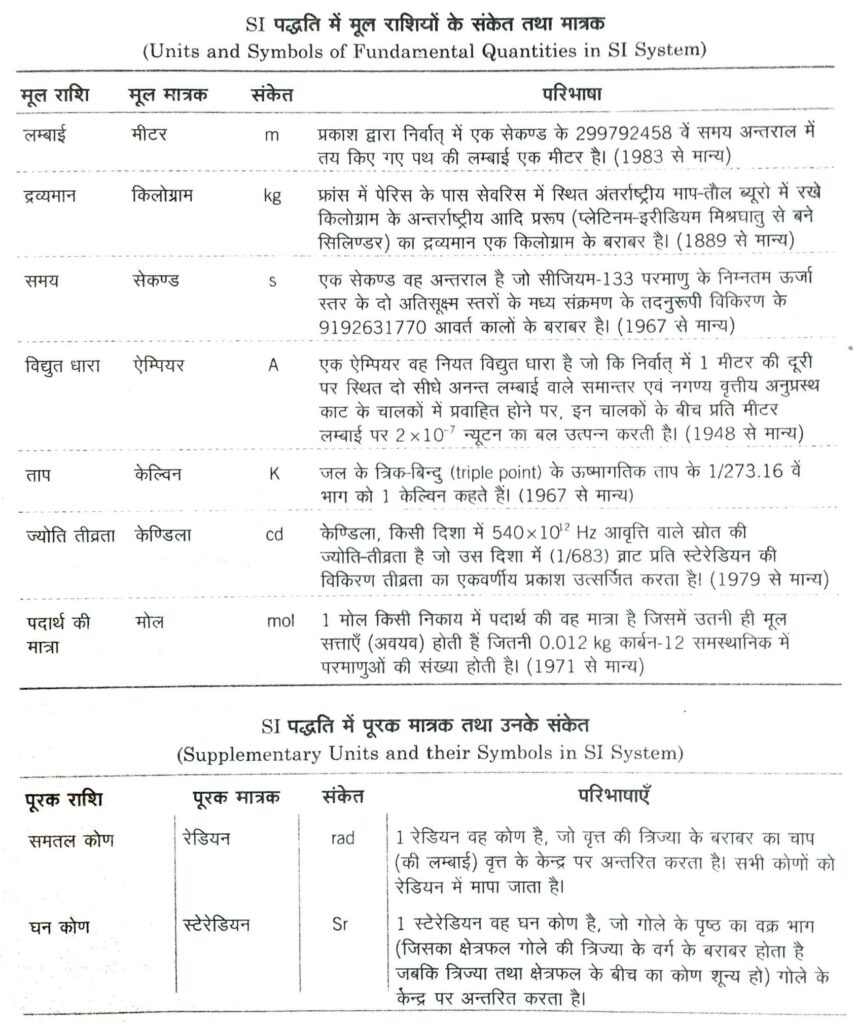


भौतिक राशियों की विमाएँ (Dimensions of Physical Quantities)
किसी भौतिक राशि के मात्रक को मूल मात्रकों के पदों में व्यक्त करने के लिए मूल मात्रकों पर जो घातें लगाई जाती हैं, वे उस भौतिक राशि की विमाएँ कहलाती हैं। भौतिक राशियों के दोनों ओर वर्ग कोष्ठक (square bracket) [ ] लगाकर भौतिक राशि की विमाएँ प्राप्त करते हैं। विमाएँ किसी राशि के परिमाण को नहीं दर्शाती हैं। उदाहरण 10 मी लम्बाई तथा 100 मी लम्बाई दोनों की विमा [L] होगी।
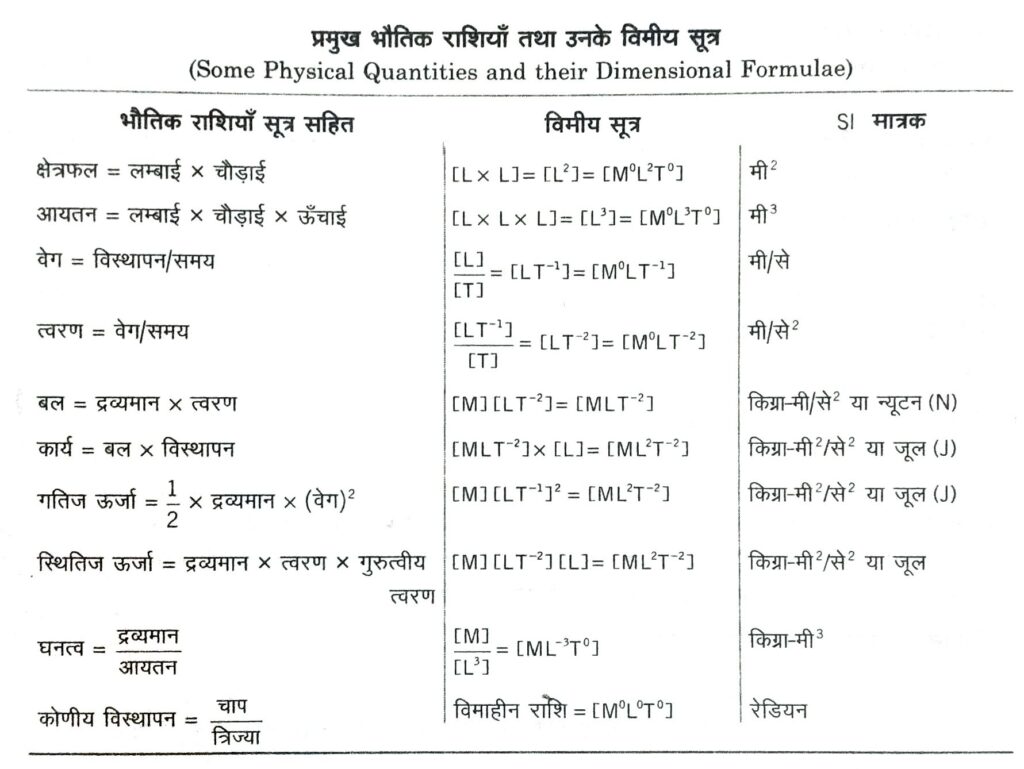
भौतिक राशियों की विमाओं का निरूपण (Dimensional Representation of Physical Quantities)
यान्त्रिकी में, लम्बाई (length), द्रव्यमान (mass), समय (time), ताप (temperature), विद्युत धारा (electrical current), ज्योति तीव्रता (luminous intensity) तथा पदार्थ की मात्रा (amount of substance) को मूल राशियों में व्यक्त करने के लिए क्रमशः [L], [M], [T], [0], [A], [cd] तथा [m या मोल] संकेतों का प्रयोग किया जाता है। व्युत्पन्न राशियों को [MLT] की विभिन्न घातों के रूप में लिखा जा सकता है, अतः M, L, T की घातों को ही उस भौतिक राशि की विमाएँ कहते हैं।

विमाहीन राशियाँ (Dimensionless Quantities)
वे भौतिक राशियाँ जिनकी विमा शून्य होती है, विमाहीन भौतिक राशियाँ कहलाती हैं। जैसे कोण, घनकोण, आपेक्षिक घनत्व, विशिष्ट ऊष्मा, पॉयसन अनुपात, विकृति, अपवर्तनांक, आदि । विमाहीन राशि का आकिंक मान सभी मात्रक प्रणालियों में समान रहता है।
विमाओं के उपयोग (Uses of Dimensions )
विमाओं के मुख्यतः तीन उपयोग होते हैं
(i) समीकरण सजातीय है या नहीं, इसकी जाँच करने के लिए।
(ii) भौतिक राशियों के बीच सम्बन्ध स्थापित करने के लिए ।
(iii) मात्रकों को एक प्रणाली से दूसरी प्रणाली में परिवर्तित करने के लिए।
◆ विमीय विश्लेषण द्वारा हमें समीकरणों में उपस्थित नियतांक का मान ज्ञात नहीं होता।
मापन में त्रुटियाँ (Errors in Measurement)
किसी राशि के मापे गए मान तथा वास्तविक मान के अन्तर को मापन में त्रुटि कहते हैं तथा मिलान करते समय त्रुटि को समाप्त नहीं किया जा सकता, इसे केवल नगण्य किया जा सकता है।
विभेदन (Resolution) विभेदन से अभिप्राय है किसी राशि का अल्पतमांक या न्यूनतम पाठ्यांक, जो यन्त्रों द्वारा पढ़ा जा सकता है।
यथार्थता (Accuracy) किसी माप की यथार्थता से अभिप्राय है कि किसी राशि का मापित मान, उसके वास्तविक मान (true value) के कितना निकट है।
परिशुद्धता (Precision) किसी माप की परिशुद्धता से तात्पर्य है कि वस्तु को किस विभेदन सीमा तक मापा गया है अथवा परिशुद्धता वह पद है जो किसी वस्तु की एक माप को उस वस्तु की अन्य मापों से निकटता प्रदर्शित करने के लिए प्रयोग किया जाता है।
त्रुटियों का वर्गीकरण (Classification of Errors)
I. त्रुटियों की प्रकृति के आधार पर
1. क्रमबद्ध त्रुटियाँ (Systematic Errors)
वे त्रुटियाँ, जो किसी एक दिशा (धनात्मक या ऋणात्मक) में निर्धारित होती हैं, क्रमबद्ध त्रुटियाँ कहलाती हैं। क्रमबद्ध त्रुटियों के कुछ स्रोत निम्न प्रकार हैं
(i) यन्त्रगत त्रुटियाँ (Instrumental Errors) वे त्रुटियाँ जो मापक यन्त्र की अपूर्ण अभिकल्पना या त्रुटिपूर्ण अंशांकन के कारण होती हैं, यन्त्रगत त्रुटियाँ कहलाती हैं।
(ii) प्रायोगिक तकनीक या कार्यविधि में अपूर्णता (Imperfection in Experiment Technique or Procedure) प्रयोग के दौरान बाह्य प्रतिबन्धों, ताप, आर्द्रता आदि में क्रमबद्ध परिवर्तन तथा मापन की अनुचित तकनीक क्रमबद्ध त्रुटियों के अन्तर्गत आते हैं।
(iii) व्यक्तिगत त्रुटियाँ (Personal Errors) ये त्रुटियाँ उपकरण की अनुचित सेटिंग तथा प्रेक्षण के दौरान व्यक्ति की लापरवाही के कारण होती हैं।
2. यादृच्छिक त्रुटियाँ (Random Errors)
मापन में अनियमित रूप से होने वाली त्रुटियों को यादृच्छिक त्रुटियाँ कहते हैं। ये त्रुटियाँ बाह्य घटकों (external factors), जैसे ताप, दाब, वायु तथा आर्द्रता द्वारा उत्पन्न होती हैं। ये त्रुटियाँ चिह्न तथा परिमाण में भी यादृच्छिक होती हैं। इस प्रकार की त्रुटि को अनेक बार प्रेक्षण लेकर उनका मध्यमान ज्ञात कर कम किया जा सकता है।
3 अल्पतमांक त्रुटियाँ (Least Count Errors)
किसी मापक यन्त्र द्वारा मापा जा सकने वाला छोटे से छोटा मान, उस मापक यन्त्र का अल्पतमांक कहलाता है। किसी मापक यन्त्र द्वारा लिए गए सभी पाठ्यांक या मापित मान उसके अल्पतमांक तक ही सही होते हैं। अल्पतमांक त्रुटि एक ऐसी त्रुटि है जो मापक यन्त्र के विभेदन से सम्बद्ध होती है। अधिक परिशुद्ध (precision) मापन यन्त्रों के प्रयोग करके, प्रायोगिक तकनीकों में सुधार आदि के द्वारा अल्पतमांक त्रुटि को कम कर सकते हैं। उदाहरण साधारण पैमाने की अल्पतमांक 0.1 सेमी है, वर्नियर कैलिपर्स की 0.01 सेमी तथा स्क्रूगेज की 0.001 सेमी है।
◆ सभी प्रकार की त्रुटियाँ सकल (gross) त्रुटियों के रूप में होती हैं।
II. मापन के गणितीय आकलन के आधार पर
1. निरपेक्ष त्रुटि (Absolute Error)
किसी भौतिक राशि के वास्तविक मान तथा मापित मान का अन्तर मापन में निरपेक्ष त्रुटि कहलाता है।
2. माध्य निरपेक्ष त्रुटि (Mean Absolute Error)
भौतिक राशि की निरपेक्ष त्रुटियों के परिमाणों के समान्तर माध्य को भौतिक राशि के मापन की माध्य निरपेक्ष त्रुटि कहते हैं।
मापन में माध्य निरपेक्ष त्रुटि = निरपेक्ष त्रुटि में प्रत्येक प्रेक्षणों का योग / प्रेक्षणों की कुल संख्या
3. आपेक्षिक या भिन्नात्मक त्रुटि (Relative or Fractional Error)
किसी राशि के मापन में निरपेक्ष त्रुटि तथा राशि के माध्य-मान का अनुपात, मापन में आपेक्षिक त्रुटि कहलाती है। यदि इस अनुपात को प्रतिशत में व्यक्त किया जाए, तो यह मापन में प्रतिशत त्रुटि (percentage error) कहलाता है।
सार्थक अंक (Significant Figures)
किसी माप में सभी विश्वसनीय (reliable) अंक तथा प्रथम संदिग्ध (doubtful) अंक को सार्थक अंक कहते हैं। उदाहरण यदि मापन के बाद किसी वस्तु की लम्बाई 574.5 मी है, तब इसमें चार सार्थक अंक 5, 7, 4, तथा 5 होंगे जिसमें 5, 7 तथा 4 तो निश्चित (certain) परन्तु अंक 5 अनिश्चित (uncertain) है।
सार्थक अंक ज्ञात करने के मुख्य नियम (Common Rules to Find Significant Figures)
(i) सभी अशून्य अंक सार्थक अंक होते हैं।
(ii) दो अशून्य अंकों के मध्य आने वाले सभी शून्य सार्थक अंक होते हैं चाहे दशमलव कहीं पर भी स्थित हो।
(iii) संख्या का मान एक से कम होने पर दशमलव के बाईं ओर तथा दशमलव के दाईं ओर प्रथम अशून्य अंक से पहले (बाईं ओर) के सभी शून्य सार्थक अंक होंगे।
(iv) यदि किसी संख्या में दशमलव नहीं है, तब अन्तिम अशून्य अंक के दाईं ओर के शून्य सार्थक अंक नहीं होते हैं।
(v) किसी संख्या में दशमलव के बाद अन्तिम अशून्य अंक के दाईं ओर के सभी शून्य सार्थक अंक होते हैं।
(vi) इकाई ( मात्रक) पद्धति बदलने से सार्थक अकों की संख्या नहीं बदलती है।
(vii) 1 से छोटी संख्या में, दशमलव के बाईं ओर लिखा शून्य कभी भी सार्थक अंक नहीं होता है।
(viii) यदि किसी संख्या में 10 की घात वाली संख्या की गुणा हो, तो इसका प्रभाव सार्थक अंकों की संख्या पर नहीं पड़ता।
सार्थक अंकों से सम्बन्धित अंकीय संक्रियाएँ (Arithmetic Operation with Significant Figures)
(i) योग तथा अन्तर (Addition and Subtraction) राशियों के योग अथवा अन्तर से प्राप्त परिणाम में दशमलव बिन्दु के बाद अकों की संख्या उतनी होगी जितनी प्रयुक्त राशियों में दशमलव बिन्दु के बाद न्यूनतम अंकों वाली राशि में होती है।
(ii) गुणा तथा भाग (Multiplication and Division) संख्याओं को गुणा अथवा भाग करने से प्राप्त परिणाम में केवल उतने ही सार्थक अंक होने चाहिए जितने कि सबसे कम सार्थक अंकों वाली मूल संख्या में हैं।
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here